Mémoire de MASTER 8 MOUTNGUI SEE
c?UYI 2010-2011.
1.3 L'équation de Boltzmann en f
Le système ?áF ái =
Ji, s'écrit donc de façon explicite :
( aÿ ) ? ?
bÿ pi
?0F 0i+ a +2 F 0i =
p0 f(t, p)ab2dp- ui R3
f(t, p)ab2dp (1.21)
b u0
R3
C'est l'équation différentielle (1.21)
qui déterminera la partie électrique F0i du
champ électromagnétique F.
1.3 L'équation de Boltzmann en f
l'équation de Boltzmann relativiste en f, pour
les particules chargées dans l'espace-
temps de Bianchi I s'écrit en notation covariante :
LXf = Q(f,f)
(1.22)
où LXf désigne la
dérivée de Lie de f par rapport au champ de vecteurs
X défini par (1.9) et Q l'opérateur
des collisions que nous introduisons ci-après. (1.22)
s'écrit donc, vu (1.9) et avec P á
défini par (1.8) :
pá ?f
?xá + Pá ?f
?pá = Q(f,f)
(1.23)
Nous considérons, le cas des collisions binaires et
élastiques du à Lichnérowicz et Cher-nikov (1940)
où, à un instant donné t et à une position
donnée (xi) de R3, seules deux particules
rentrent en collision à la fois, sans se détruire l'une et
l'autre, la collision affectant seulement l'impulsion de chaque particule qui
n'est plus la même avant et après le choc, seule la somme des 2
impulsions est conservée, suivant le schéma:
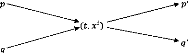
L'opérateur des collisions Q est alors
défini de la façon suivante, en prenant en compte cette situation
et en désignant par p, q les impulsions avant le choc, par
p', q' les impulsions après le choc et en utilisant
deux fonctions f et g sur R3 :
Q(f, g) = Q+(f,
g) - Q-(f, g) (1.24)
1.3 L'équation de Boltzmann en f
{ Q+(f, g)(p) = f
$3 abq0dq fS2
f(p')g(q')ó(t,
p, q, p', q')dù (1.25)
où : Q (f, g)(p) =
f$3 a q0
q fS2
f(p)g(q)ó(t, p, q,
p', q')dù (1.26)
formules dont nous présentons les
éléments étape par étape, en précisant les
hypothèses adoptées :
· S2 désigne la sphère
unité de R3 dont l'élément d'aire est
noté dù
· ó est une fonction positive et
régulière de tous ses arguments appelée noyau de la
collision ou section efficace de choc.
Nous faisons sur ó les hypothèses
suivantes. Il existe une constante C1 > 0 telle que :
{
0 < ó(t, p, q, p',
q') < C1
|ó(t, p1, q,
p', q') - ó(t,
p2, q, p', q')| <
C1|p1 - p2| (1.27)
3
où |p| = Ei)
[1(p2]
|
2
|
désigne la norme euclidienne sur R3
|
|
· Mémoire de MASTER 9
MOUTNGUI SEE c?UYI 2010-2011.
La loi de conservation p + q =
p' + q' se scinde en :
{
p0 + q0 =
p'0 + q'0
(1.28)
p + q = p' +
q' (1.29)
(1.28) exprime la conservation de la quantité
:
v v
?e = 1 +
a2(p1)2 +
b2[(p2)2 +
(p3)2] + 1 +
a2(q1)2 +
b2[(q2)2 +
(q3)2] (1.30)
appelée énergie élémentaire des
particules de masse propre au repos m = 1. Quant à
(1.29), on l'interprète en posant, suivant R. T. Glassey dans
[5] :
{
p' = p + C(p, q,
ù)ù (ù E S2)
(1.31)
q' = q -
C(p,q,ù)ù
où C(p, q, ù) est une fonction
scalaire de ses arguments.
On montre en utilisant (1.6) pour exprimer
p'0 et q'0, en
fonction de p' et q', puis
(1.31) pour exprimer p' et q'
en fonction de p et q que l'équation (1.28)
conduit à une équation du second degré en
C(p, q, ù), dont la seule solution non triviale est
donnée par :
2p0q0?e ù
· (?q - ?pl
C(p, q, ù) =
(1.32)
?e2 - [ù ·
(p + q)]2
| 


