Existence globale des solutions du système couplé maxwell-boltzmann-euler sur un espace temps de Bianchi I.

CHAPITRE DEUX

EXISTENCE LOCALE DES

SOLUTIONS

Notre objectif est d'appliquer au système différentiel (S) la théorie des systèmes différentiels du premier ordre. A` cet effet, nous prouverons que les fonctions définies par (S) sont continues par rapport à la variable t et localement lipschitzienne par rapport à X = (E, p, f, u) pour la norme de l'espace de Banach E = 118³ × 118³ × L¹(118³) × 118³

Proposition 2.1. Soit f, g ? L¹(118³) ; alors _p01 Q⁺(f, g), _p01 Q^-(f, g), _p01 Q(f, g) appartiennent à L¹(118³) et :

? p01 Q⁺(f, g)? = C(t)?f??g?; ? p0 1 Q^-(f, g)? = C(t)?f??g? (2.1)

? _p0¹Q⁺(f, f) - _p0Q⁺(g,g)? =C(t)(?f? + ?g?)?f - g? ¹(2.2)

?_p0¹Q^-(f,f) -_p0Q^-(g,g)? =C(t)(?f? + ?g?)?f -g? ¹(2.3)

? 11

_p0Q(f, f) - _p0Q(g,g)? = 2C(t)(?f? + ?g?)?f - g? (2.4)

où C(t) = 4ðC1ab²(t), C1 > 0 étant la constante fournie par (1.27). Preuve.

1. L'expression (1.25) de Q+(f, g) donne, en utilisant la majoration (1.27) de ó par C1 :

?_p0Q⁺(f,g)? = C1ab2(t)f3fR3 dp°d0q J s2 |f (a)

Le Jacobien (1.33) du changement de variables (p, q) ? (p^', q^') donne p0e P e ^dp_g00 = ^d₂:0^'

'0 _q'0^'

Mémoire de MASTER 19 MOUTNGUI SEE c?UYI 2010-2011.

Nous avons de (a), en utilisant ¹

_p'0_q'0 = 1 d'après (1.6) :

?_p0¹Q⁺(f,g)? = C1ab²(t)J I_.Î(P')I dP' f 3 I9(q')I dq'du)J ₂ d

3

= 4ðC1ab²(t)?f??g?

d'où la première inégalité.

De même l'expression (1.26) de Q^-(f, g), l'inégalité (1.27) et ¹

p0q0 = 1 donnent :

_{J J J}

? p0 1 Q^-(f,g)? = C1ab2(t) _R3 |f(p)|dp _R3 |g(q)|dq _S2 dù

= 4ðC1ab²(t)?f??g?

d'où (2.1)

2. Les expressions (1.25) et (1.26) de Q+ et Q- montrent que Q+, Q- ainsi que Q sont des opérateurs bilinéaires.

? ? _p0¹Q⁺(f,f)- _p0Q⁺(g,g)? =? 1

1 p0 Q⁺(f,f-g)+ _p0¹Q⁺(f - g, g)?
=?_p0¹Q⁺(f,f-g)?+?_p0¹Q⁺(f-g,g)?

= C(t)?f??f - g? + C(t)?g??f - g?

= C(t)(?f? + ?g?)?f - g?

d'où (2.2)

? ?_p0¹Q^-(f, f) - _p0Q^-(g, g)? = ?1

1 _p0Q^-(f, f - g)

+ _p0¹Q^-(f - g, g)?

= ?_p0¹Q^-(f, f - g)? + ?_p0¹Q^-(f - g, g)?

= C(t)?f??f - g? + C(t)?g??f - g?

= C(t)(?f? + ?g?)?f - g? d'où (2.3)

? ? _p0¹Q(f, f) - _p0Q(g, g)? = ?(¹

1 _p0Q⁺(f, f) - _p0¹Q^-(f, f)) - (_p0¹Q⁺(g, g) - _p0¹Q^-(g, g))?

= C(t)(?f? + ?g?)?f - g? + C(t)(?f? + ?g?)?f - g?

= 2C(t)(?f? + ?g?)?f - g?

d'où (2.4)

Proposition 2.2. Soit p = (p^z), u = (u^z), p_i = (p^z_i), ui = (u^z_i) ? 118³, j = 1, 2, f ? L¹(118³). Alors :

=

_p0Q⁺(f, f) - p0 Q⁺(g, g)) + (1

1 _p0Q^-(g, g) - _p0¹Q^-(f, f))?

= ? 1

p0 Q⁺(f, f) - p0 Q⁺(g, g)? + ? 1

1 p0 Q^-(f, f) - p0 1Q-(g,g)?

?( 1

p0 = a|p1|; p⁰ = b|p2|; p⁰ = b|p³| (2.5)

u0 = a|u1|; u⁰ = b|u2|; u⁰ = b|u³| (2.6)

p^k₂

p⁰₂

_uk

2

u0 ₂

????

p^k₁

p0 ₁

????

_uk

1

u⁰₁

????

????

????

p0 ₁

1

p⁰₂

1

????

1

1

0

_u0

2

u 1

?( )

??1 + a

? = 5 b + b ?p₁ - p₂? (2.7)
a

?( )
??1 + a

= 5 b + b

? ?u1 - u2? (2.8)
a

=

p^k₁p⁰₂ - p^k₂p⁰₁

p⁰₁p⁰₂

p^k₁(p⁰₂ - p⁰₁) + p⁰₁(p^k₁ - p^k₂)

p⁰₁p⁰₂

????

p^k1 p0 1

p^k2 p^02

????

= =

???? ????

????

????

(2a + 4b)?p1 -₀ p2?, j = 1, 2 (2.9)
p_i

= (2a + 4b)?u1 -₀ u2?, j = 1, 2 (2.10)
u_i

? 1 1

₀Q(f, f,p₁) - ₀Q(f, f,p₂)? = 8ðC1ab²?f?²?p₁ - p₂?, j = 1,2 (2.11)

p_i p_i

où C1 > 0 est la constante donnée par (1.27).

Preuve. Remarquons que d'après (1.6) et (1.13), il nous suffit de prouver les inégalités en p et la proposition en découlera.

1. (2.5) est une conséquence directe de l'expression (1.6) de p0

2. Soit k ? {1, 2, 3}

Mémoire de MASTER 20 MOUTNGUI SEE c?UYI 2010-2011.

En utilisant p⁰₂ = 1, on déduit :

|p^k₁||p⁰₂ - p⁰₁| =+|pk ₁ -p^k ₂| (a)

p⁰₁p⁰₂

????

p^k₂

p^k₁

p0 ₁

p⁰₂

????

En utilisant l'expression (1.6) de p⁰ :

₂)²

p0 1 - p0 2 = (p⁰ ₁)² - (p0 0

p⁰₁ + p₂

a2(p1 ₁ + p¹ 2)(p1 1 - p¹ ₂) + b2(p2 ₁ + p² 2)(p2 1 - p² ₂) + b2(p3 ₁ + p³ 2)(p3 1 - p³ ₂)

=

(b)

p0 1 + p0 ₂

Nous avons de (a) et (b) :

????

p^k1 p^01

k p2 p^02

????

=

[a²(|pp¹₁| + |p^k₁p¹₂|) + b²(|p^k₁p²₁| + |p^k₁p²₂|) + b²(|p^k₁p³₁| + |pk1p32|) + 1] ?p₁ - p₂?(c)

p⁰₁p⁰₂(p⁰₁ + p02) J

Nous avons en utilisant convenablement les inégalités (2.5) : Pour k = 1 :

|p^11|^2 + |p^11p^12| p^01p^02(p^01 + p02) =

2 |p^11p^21| + |p^11p^22| 2 |p^1 1p^3 1| + |p^1 1p^3 2| 2 a2; p0 1p^0 2(p0 1 + p^0 2) = ab; p^0 1p^0 2(p0 1 + p^0 2) = ab

Pour k = 2 :

|p²₁p¹₁| + |p²₁p¹₂| p⁰₁p⁰₂(p⁰₁ + p02) =

Pour k = 3 :

|p³₁p¹₁| + |p³₁p¹₂| p⁰₁p⁰₂(p⁰₁ + p02) =

(c) donne alors :

2 |p²₁|² + |p²₁p²₂| 2 |p² ₁p³ ₁| + |p² ₁p³ ₂| 2

ab; p⁰ ₁p⁰ 2(p0 ₁ + p⁰ 2) = b2 ; p0 ₁p⁰ 2(p0 ₁ + p⁰ 2) = b2

2 |p³₁p²₁| + |p³₁p²₂| 2 |p³ ₁|² + |p³ ₁p³ ₂| 2

ab; p⁰ ₁p⁰ 2(p0 ₁ + p⁰ 2) = b2 ; p⁰₁p⁰₂(p⁰₁ + p02) =b2

????

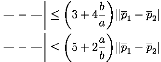
p¹₁

p⁰₁

p¹₂

p⁰₂

????

2

p²₁

p 2

p0 ₁

p⁰₂

=(5 + 2)?p₁ - p₂? b

????

3

p 2

p0 ₁

p³₁

p⁰₂

=

(3 + 4b)?p1 - p2? a (5 + 2)?p1 - p2?

b

Mémoire de MASTER 21 MOUTNGUI SEE c?UYI 2010-2011.

or

3 + 4b a

( ) 1 + a = 5 b + a b

( )

5 + 2a b = 5 + 5^a 1 + a

b =5 b + a b

d'où :

?( )

??1 + a

= 5 b + b

? ?p₁ - p₂?, k = 1, 2, 3
a

????

p^k₂

p^k₁

p⁰₁

p⁰₂

????

3. Nous avons en utilisant l'expression (1.6) de p⁰ et (b) :

????

1 p^01

1 p^02

????

??_?(p⁰₁)² - (p⁰₂)² ?= ???p⁰₁p⁰₂(p⁰₁ + p02) ?

= ????

????

a²(p¹₁ + p¹₂)(p¹₁ - p¹₂) + b²(p²₁ + p²₂)(p²₁ - p²₂) + b²(p³₁ + p³₂)(p³₁ - p³₂)

p⁰₁p⁰₂(p⁰₁ + p⁰₂)

a²(|p¹₁| + |p¹₂|) + b²(|p²₁| + |p²₂|) + b²(|p³₁| + |p³₂|)

= ?p₁ - p₂? (d)
p⁰₁p⁰₂(p⁰₁ + p⁰₂)

En utilisant (2.5) et p⁰_j = 1, j = 1,2 :

|p^11| + |p^12| p01p0 2(p01 + p^0 2) =

2 |p^2 1| + |p^2 2| 2 |p^3 1| + |p^3 2| 2 ; ap0 p^0 1p^0 2(p0 1 + p^0 2) = ; bp^0 2) = , j = 1,2 (e) p0 1p^0 2(p0 1 + p^0 bp^0 j j j

(d) et (e) donnent :

????

1 p^01

1 p^02

????

= (2a + 4b)?p1 - p2? ,j = 1,2

p⁰_j

??

??

?= ?

? ?

???????+ ?

4.

????

Q(f, f,p₁) - Q(f, f,p₂)

p⁰_j

Q⁺(f, f,p₁) - Q⁺(f, f,p₂)

p_j

0

Q^-(f,f,p₁) - Q^-(f, f,p₂)

p⁰_j

Mémoire de MASTER 22 MOUTNGUI SEE c?UYI 2010-2011.

L'expression (1.25) de Q⁺ donne :

???? =

????	Q^+(f, f,p1) - Q^+(f, f,p2)
	pj 0

?? dù

|f(p^')||f(q^')| ?_?ó(t, p₁, q, p^', q^') ? ó(t, p₂, q, p^', q^')

1 /' ab2dq~ p_j R3 g⁰ s2

En utilisant la seconde inégalité (1.27) du noyau de la collision ó et en procédant comme dans la preuve de la première inégalité (2.1), on obtient :

? ? ? ? ?Q^+(f,f,p1) - Q+(f,f,p2) ? ? p0 ? j			= 4ðC1ab^2?f?^2?p1 - p2?
De même on obtient : ? ? ? ? ?Q^-(f, f,p1) - Q^-(f, f,p2) ? ? p0 ? j d'où :		= 4ðC1ab^2?f?^2?p1 - p2?
? ? ? ? ?Q(f, f, p1) - Q(f, f, p2) ? ? p0 ? j	= 8ðC1ab^2?f?^2?p1 - p2?, j = 1, 2

Proposition 2.3. Soit

X1 = (E1,p₁, f1, u1) ? E = 118³ × 118³ × L¹(118³) × 1[8³

X2 = (E2, p₂, f2, u2) ? E

alors il existe des constantes C2, C3, C4, C5, C6 telles que :

?G1(t,X1) - G1(t,X2)?63 = C2(?E1 - E2? + ?f1 - f2? + ?u1 - u2?) (2.12) ?G2(t, X1) - G2(t, X2)?63 = C3(?E1 - E2? + ?p₁ - p₂? + ?f1 - f2? + ?u1 - u2?) (2.13) ?G3(t, X1) - G3(t, X2)?L¹(6³) = C4(?p₁ - p₂? + ?f1 - f2?) (2.14) ?G4(t, X1) - G4(t, X2)?63 = C5(?E1 - E2? + ?f1 - f2? + ?u1 - u2?) (2.15) ?G(t, X1) - G(t, X2)? = C6?X1 - X2? (2.16)

où

{

?X1 - X2? = ?E1 - E2? + ?p₁ - p₂? + ?f1 - f2? + ?u1 - u2?

C2=10(1+C)(1+ab²)(1+^a_b+_a^b+¹_a+¹_b)(1+?f2?)

C3 = 10(1 + C)(1 + a + b)⁴(1 + ^ab + ^ab + ^a1 + ¹_b)²(1 +?E1?)(1 +?f2?)(1 + ? ij |öij|)

C4 = 16ðC1ab²(1 + a + 2b)(1 + ?f1? + ?f2? + ?f2?²)

C5 = 200

ñ0 (1 + C)(1 + ñ0)(1 + a + b)⁵(1 + ^ab + ^ba + ^a1 + ¹_b)²(1 + ?E1? +?E2?)(1 + ?f1? + ?f2?)×

(1 + ?u1? + ?u2?)(1 + >ij |öij|)

C6 = C2 + C3 + C4 + C5

(2.17)

Preuve.

Mémoire de MASTER 23 MOUTNGUI SEE c?UYI 2010-2011.

Mémoire de MASTER 24 MOUTNGUI SEE c?UYI 2010-2011.