Réalisation d'un robot mobile avec évitement d'obstacle et trajectoire programmée.

3.5. L'approche locale

Les techniques locales n'utilisent pas de modèle complet de l'espace libre. Elles sont sans mémoire, et ne prennent en compte à une instante donne que l'environnement proche du mobile pour modifier une trajectoire de consigne.

Ces méthodes sont attrayantes par leur simplicité, bien sûr elles présentent un inconvénient majeur de ne pas pouvoir suivre le chemin optimal. Le système peut être bloqué par des dispositions concaves d'obstacle. Ces méthodes sont beaucoup moins couteuses et ne utilises

Chapitre 03

Planification de localisation et trajectoire

pour acquérir des informations nécessaires au fur et à mesure de déplacement les méthodes locales existantes sont [14]:

· Méthode de champs de potentiel.

· La méthode myopique.

3.5.1. Méthode myopique

Cette méthode est inspirée du comportement d'un aveugle évoluant dans un environnement inconnu en détectant les parois des obstacles avec sa canne. L'algorithme de contournement d'obstacle permet au robot mobile d'évoluer en fonction des informations issues des capteurs. II part de l'hypothèse que s'il existe un chemin entre un point initial P_o et un point finale P_n l'algorithme est capable de le déterminer en longeant les obstacles présents sur la trajectoire du robot. Si le lieu d'évolution ne comporte pas d'obstacle entre les points de départ et d'arrivée, la trajectoire est la droite passant par les points P_o (X_o, Y_o) et Pn (X_n,Y_n) . La figure 3.6 représente cette méthode [12].

En présence d'obstacles, on définit des points intermédiaires en fonction des obstacles, à contourner. L'ensemble des segments joignant ces points constitue la trajectoire de contournement.

X

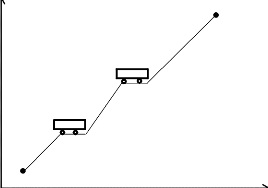
Pn(Xn,Yn)

P2 (X2,Y2)

P1(X1,Y1)

P_o (X_o,Y_o)

Y

35

Figure 3.6 : Contournement dans le cas de la méthode myopique.

Chapitre 03

Planification de localisation et trajectoire

36

3.5.2. Méthode de champs de potentiel

La méthode considère que le mobile évolue dans un champ de forces dont le but est un pôle attractif alors que les obstacles sont répulsifs. L'amplitude de la force de répulsion est une fonction de l'inverse de la distance entre le mobile et l'obstacle alors que la force d'attraction est une fonction de la distance à parcourir jusqu' au but [14].

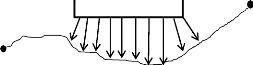
Obstacle

Arrive

Départ

Figure 3.7: Principe d'évolution d'un robot mobile par la méthode de champs de potentiel

5. Evitement des obstacles en logique floue