Robot mobile avec suivi visuel de ligne

I.5.1. Le modèle cinématique du robot de type uni-cycle:

(a) (b)

Figure .I.6: Robot mobile: (a) MIABOT, (b) Pioneer P3-DX.

Le modèle d'un robot mobile uni-cycle correspond à celui d'une roue roula

La configuration de l'uni-cycle e caractérisée par la donnée es nombres

Où x et y dénotent les coordonné cartésiennes du point de ntact de la roue avec le sol

dans un repère cartésien donné, orientation de la roue et 'angle de la roue mesurée à

partir de la verticale. Sach u ement est sans glissement le modèle cinématique

de la roue s'exprime par van

0 ( )

0

Où r représente le rayon de la roue.

Le modèle (1.1) peut être transformé pour faire apparaître les composantes des vitesses

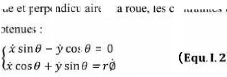
dans les plans de la roue peenule à l l contraintes cinématiques
suivantes sont alors obs

s =

Ces deux équations sont des contraintes de type non holonome, signifiant que l'on ne peut pas les intégrer de façon à ne faire apparaître que les coordonnées généralisées. Cela peut

8

Robot Mobile Avec Suivi Visuel De Ligne

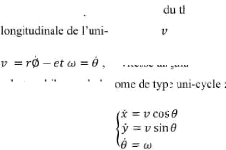
Chapitre I : Généralités Sur Les Robots Mobiles

se démontrer simplement à l'aide héorème de Frobenius. En notant la vitesse

it cycle avec

sa vitesse angulaire, on déduit de (1.1) le modèle cinématique du

robot mobile non-holono e

( )

I.5.2. Le modèle cinématique de type voiture : Un robot mobile de type voiture est composé d'un train moteur à l'arrière du corps principal et de deux roues de direction et à

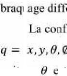
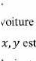
bu érentiel à l'avant (Figure. I.7)

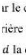
iguration du véhicule de type v peut être représentée pa quadruplet

[ Ø] , où le point de cordonnées le centre de l'essieu arr de la

voiture, st l'orientation du véhicule, Ø l'orientation des roues avant et distance
entre les essieux avant et arrière.

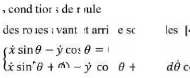
ins oment sans glissement s'obtient éivant que les vitesses

Les

latérales u a e ère ont null 4]:

s 0

( )

( +y Ø)

s( + Ø) - os Ø = 0

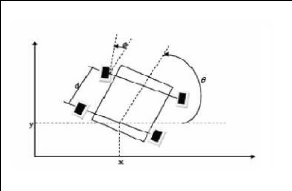
Figure. I.7: Robot mobile de type voiture.

Ces contraintes sont non intégrables, le véhicule de type voiture est donc non holonome.

9

Robot Mobile Avec Suivi Visuel De Ligne

Chapitre I : Généralités Sur Les Robots Mobiles

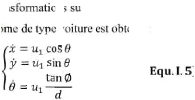
En utilisant des tranons r l'équation(1.4) , le modèle cinématique d'un

robot mobile non-holono v enu :

( )

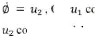
Où orrespond à la vitesse longitudinale du corps du robot, alors que

rrespond à la vitesse angulaire des roues directrices par rapport au corps du véhicule.

I.6. LES DIFFERENTS TYPES DE TERRAIN:

Nous rencontrons principalement 3 types d'espaces de navigation : les terrains plats, les Terrains accidentés et les espaces 3D. Les terrains plats sont généralement utilisés pour modéliser les milieux urbains et les intérieurs de bâtiments. Le robot évolue sur un plan 2D considéré sans pentes, et tout objet qui sort de cet espace 2D est considéré comme un obstacle (Figure. I.8).

Cette représentation est la plus simple à étudier et la plus répandue pour les robots mobiles aux roues. En première approche, elle permet de se concentrer sur les problèmes de contrôle et de navigation autonome du robot.

Figure. I.8 : Robucab [10].

Les terrains accidentés (ou 2D 1 /2) correspondent généralement aux milieux en extérieurs, comme des forêts, des champs en robotique agricole, ou encore des terrains rocheux (Figure. I.9). La différence avec les terrains plats est la présence des pentes, de bosses et de creux sur le terrain d'évolution du robot.

10

Robot Mobile Avec Suivi Visuel De Ligne

Chapitre I : Généralités Sur Les Robots Mobiles

Cela interdit d'utiliser une métrique standard 2D et cela complique pour beaucoup la détection d'obstacles et la modélisation des déplacements du robot. De plus il devient également important de vérifier que le robot ne bascule pas quand il escalade une pente ou enjambe un obstacle. Le système de locomotion du robot doit dans ce cas être adapté à la topologie du terrain.

Figure. I.9 : Le robot martien Sojouner [5].

Enfin les espaces d'évolution 3D sont par exemple utilisés pour modéliser la navigation des robots sous-marins (Figure. I.10) et des drones volants (Figure. I.11). Les problèmes rencontrés sont spécifiques à l'application visée.

Chaque type de terrain correspond à des problématiques bien spécifiques. Le type de robot étudié dans ce mémoire est celui destiné à circuler en environnement urbain, la modélisation terrain plat sera utilisée. Cela signifie que l'on considère que tous les mouvements sont contenus dans un plan de navigation, parallèle au sol.

Figure. I.10 : Le robot sous marin TAIPAN [12].

11

Robot Mobile Avec Suivi Visuel De Ligne

Chapitre I : Généralités Sur Les Robots Mobiles

Figure. I.11 : Drone de surveillance RESSAC de l'ONERA [8].

I.7. LOCALISATION:

Les outils permettant la localisation d'un robot dans son environnement peuvent être classés en deux catégories : ceux par localisation à l'estime et ceux par localisation absolue [5]. Le principe de la première catégorie consiste à intégrer des informations sur les vitesses ou les accélérations fournies par des capteurs proprioceptifs (odomètres, centrales inertielles).

L'avantage de ces méthodes est qu'elles sont indépendantes de l'environnement, par contre leur souci est leur manque de précision dû à la dérive temporelle. En effet les Erreurs s'intégrant elles aussi au fur et à mesure du temps. Il est nécessaire d'apporter régulièrement des recalages (Figure. I.12).

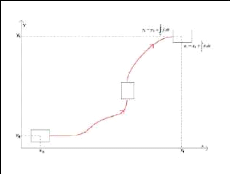
Figure. I.12 : Localisation à l'estime.

12

Robot Mobile Avec Suivi Visuel De Ligne

Chapitre I : Généralités Sur Les Robots Mobiles

Parmi les méthodes de localisation à l'estime, le système le plus simple et le plus couramment utilisé pour la mesure de déplacement du robot est l'odométrie.

L'hypothèse de roulement sans glissement que nous avons vu précédemment, nous permet de relier directement les déplacements du robot à la vitesse de rotation des roues. Par intégration des déplacements à chaque instant, on en déduit la position relative du robot par rapport à son point de départ. L'odométrie est une méthode de localisation très courante, simple, mais également très rapidement imprécise.

En effet à cause du glissement des roues sur le sol, les erreurs s'accumulent au fur et à mesure que le robot avance, ce qui implique d'importantes erreurs sur les longs parcours s'il n'y a pas de recalage régulier.

Cette méthode est de ce fait fortement tributaire de la qualité du sol sur lequel le robot se déplace. Les incertitudes sur le diamètre exact des roues, sur les paramètres géométriques du robot, sur la résolution des codeurs, génèrent des erreurs de type systématique, qui vont s'accumuler très rapidement en odométrie.

Cependant, ces erreurs peuvent être identifiées et évaluées pour faire un rééquilibrage du système et ainsi améliorer sa précision. Les erreurs non systématiques comme les glissements ou les irrégularités du sol, génèrent moins rapidement des erreurs, mais ne peuvent par contre pas être rééquilibrées puisqu'on ne peut pas les prévoir.

Pour l'exploration martienne, où le terrain est fortement accidenté, l'utilisation de

Système d'odométrie classique est impossible. Pour cette application, Cheng a proposé une technique d'odométrie alternative, dite odométrie visuelle, basée sur la reconnaissance de points singuliers dans l'image vidéo du sol fournie par une caméra montée sur le robot [5] (les points de Harris).

Connaissant le positionnement de la caméra par rapport au robot, le déplacement de ces points dans l'image permet d'évaluer les vitesses de déplacement du robot, et par intégration, de retrouver sa localisation relative par rapport à sa position initiale.

Le second type de méthode pour la localisation est la localisation absolue. Ces méthodes utilisent des éléments repérables par le robot dans l'environnement de navigation, de position

Connue, pour permettre au robot de se repérer relativement à ceux-ci. Ces éléments sont appelés des balises ou amers et sont dits soit réels, s'ils ont été placés spécialement pour permettre la localisation, soit virtuels s'il s'agit d'éléments présents naturellement.

13

Robot Mobile Avec Suivi Visuel De Ligne

Chapitre I : Généralités Sur Les Robots Mobiles

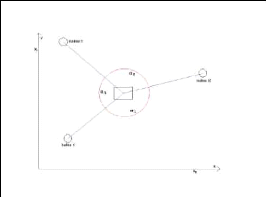
Les balises réelles sont dites passives si elles ont pour but de réfléchir un signal émis par un appareil de mesure du robot (laser ou infrarouge). Il existe deux méthodes pour utiliser ces balises pour la localisation du robot : la méthode télémétrique (calcul de la distance robot/balise), qui nécessite la présence de deux balises pour calculer la position du robot dans le plan ; et la méthode par triangulation, qui consiste à mesurer les angles entre chaque balise et le robot, et qui elle nécessite l'utilisation de 3 balises.

Figure. I.13 : Localisation absolue (méthode par triangulation).

Les balises réelles sont dites actives si elles émettent un signal captable par le robot. En Milieu extérieur, le système GPS (global positionning system) peut être utilisé pour obtenir des positions d'une précision de l'ordre du mètre.

A la base développée par l'armée américaine dans les années 80 (lancement du premier satellite GPS en 1978), il fut ouvert aux civils en 1995. Jusqu'en 2000 les mesures étaient volontairement entachées d'une erreur d'une centaine de mètres, l'armée américaine craignant que ce système soit un avantage pour leurs ennemis. Malgré le retrait de cette erreur volontaire, la précision du système restait de l'ordre du mètre, à cause des incertitudes sur l'orbite et l'horloge des satellites, ainsi que les retards engendrés par la traversée des couches atmosphériques.

Pour améliorer cette précision, nous pouvons utiliser les GPS différentiels : avec un second récepteur GPS sur une base fixe et de position connue. Il devient possible de mesurer l'erreur et d'en déduire la correction à apporter pour la zone environnante, pour que ce système fonctionne, il faut que la base mobile reste à une certaine portée de la base fixe. Cette distance varie suivant la gamme de fréquence utilisée pour l'envoi des

14

Robot Mobile Avec Suivi Visuel De Ligne

Chapitre I : Généralités Sur Les Robots Mobiles

corrections, et peut atteindre quelques dizaines de kilomètres pour les besoins de la navigation maritime.

Des satellites géostationnaires permettent également de corriger certaines erreurs de position. Ils envoient des corrections sur les orbites et les horloges des satellites GPS.

Ainsi pour l'Europe c'est le système EGNOS (European Geostationary Navigation Overlay System) qui se charge d'envoyer ces corrections. La précision atteinte est de l'ordre de 3m. Le système de GPSRTK (real time kinematics) permet d'améliorer la précision à quelques centimètres, en utilisant la différence de phase de l'onde porteuse du signal, sa longueur d'onde étant d'une vingtaine de centimètres.

En contre partie la portée de la station de référence avec cette méthode n'est plus que de quelques kilomètres. Pour augmenter cette portée on a recours au RTK réseau, qui va utiliser la redondance d'informations pour communiquer les corrections à l'appareil, via un serveur de calcul à distance. Les systèmes de localisation GPS sont très intéressants en rase campagne ou en banlieue.

Cependant ils s'avèrent beaucoup moins efficaces en pleine ville ou en forêt. En effet pour fonctionner correctement un GPS a besoin de recevoir les informations de 4 satellites au moins.

La présence d'obstacles tels que les ponts et grands bâtiments en ville empêche parfois cette réception. Ainsi il n'est pas rare de perdre la localisation GPS pendant quelques minutes. C'est pour cela que beaucoup de recherches dans le domaine de la localisation sont aujourd'hui portées sur les méthodes alternatives au GPS en milieu urbain. La vision peut être un moyen pour compléter la localisation par GPS. Ainsi Cappella [6].

Utilise un modèle 3D de la place Stanislas à Nancy qui est confronté aux images obtenues par les caméras embarquées sur le robot pour déterminer précisément sa position. Yang propose d'utiliser les caméras du robot pour mettre au point un système d'odométrie visuelle [7].

I.8. PLANIFICATION DE TRAJECTOIRE:

* Chemin: Un chemin entre une situation initiale XI et une situation finale XF est une représentation géométrique du d'emplacement du corps qui ne considère pas le temps [8].

I.8.1. Approches polynomiales pour la génération de trajectoires: Différentes méthodologies de planification basées sur l'utilisation de trajectoires Polynomiales. Par exemple, l'utilisation de courbes de type spline ou B-spline. La trajectoire est conçue en

15

Robot Mobile Avec Suivi Visuel De Ligne

Chapitre I : Généralités Sur Les Robots Mobiles

prenant en compte les contraintes cinématiques du robot mobile ainsi que la position des différents obstacles statiques à éviter.

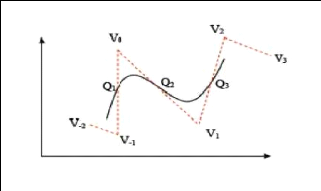
Une trajectoire générée par une courbe B-spline peut-être représentée à titre d'exemple comme sur la Figure. I.14.

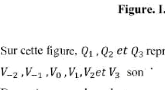
14 : Courbe B-spline.

résentent les points de passage de la courbe et

t les points qui forment le polygone de contrôle de la courbe. En pratique pour les robots mobiles de type uni-cycle ou véhicule, les B-splines cubiques s'avèrent être un choix suffisant pour définir une trajectoire vérifiant les contraintes cinématiques.

Une autre famille de trajectoires fréquemment utilisées pour la planification des robots mobiles non-holonomes est basée sur l'utilisation des courbes de Bézier. Un exemple de courbe de Bézier cubique est représenté sur la Figure. I.15.

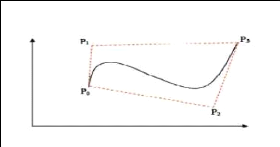
Figure. I.15 : Courbe de Bézier cubique.

16

Robot Mobile Avec Suivi Visuel De Ligne

Chapitre I : Généralités Sur Les Robots Mobiles

Les points stituent le polygone de contrôle de la courbe [4].

I.8.2. Carte routière (road map) :

Cette approche est basée sur l'identification d'un ensemble de routes dans l'espace libre. La base de cette approche est de capturer la connectivité de l'espace libre d'un robot dans un réseau de dimension 1 de courbes ou de lignes appelée carte routière. Une fois la carte routière construite, elle est utilisée comme étant un réseau de segments de routes (chemin) pour la planification des mouvements des robots.

L'objectif de cette approche est de construite un réseau routière qui rend le robot capable à visiter tous les points possible de l'environnement libre de navigation. On note qu'il y a deux approches différentes pour la construction de la carte routière. Dans le premier cas les routes sont le plus proche possible de l'obstacle, d'où l'appellation de « Graphe de visibilité » les chemins qui résultent sont de longueur minimum; le deuxième cas est appelé « diagramme de Voronoi » les routes restent le plus loin possible de l'obstacle [9].

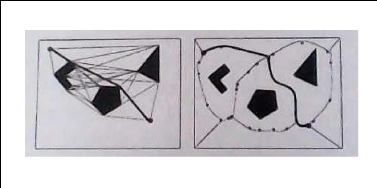
Figure. I.16 : Graphe de visibilité (à gauche) et diagramme de Voronoi (à droite).

I.8.3. Approche globale: Elle est utilisée lorsque le robot évolue dans un environnement entièrement connu. Le principe de cette approche est de capturer la connexité globale de l'espace libre dans un graphe qui est ensuite exploré. La connaissance de l'environnement nécessite sa modélisation:

17

Robot Mobile Avec Suivi Visuel De Ligne

Chapitre I : Généralités Sur Les Robots Mobiles

I.8.3.1. Approche Par squelette:

Un squelette est une concaténation de portions de courbes. Il est structuré en un graphe dont les arêtes sont ces portions de courbes et les noeuds leurs extrémités.

Il existe plusieurs types de squelettes entre autres : les graphes de visibilités et les `freeways' :

Graphe de visibilité: Les noeuds du squelette sont les sommets des obstacles, tandis que les arêtes sont les segments joignant deux à deux les sommets visibles. Les `freeways': L'espace libre est divisé en un ensemble de cônes dont les axes constituent les `freeways' que le robot va pouvoir suivre. Les arêtes du graphe représentent les `freeways', alors que les noeuds sont leurs extrémités.

Les méthodes se basant sur une approche globale ont l'avantage de générer un chemin optimal tandis qu'elles ont l'inconvénient de consommer beaucoup de temps de calcul et d'espace mémoire [10].

I.8.4. Approche locale : Contrairement à l'approche globale, cette approche ne nécessite pas une connaissance a priori de tout l'environnement, mais découvre celui ci au fur et à mesure à l'aide de systèmes de perception.

Cette approche est itérative (incrémentale). A chaque itération, on détermine l'incrément du déplacement. A titre d'exemple on peut citer deux méthodes [10] : I.8.4.1. Méthodes des champs de potentiel : Le robot est assimilé à un point plongé dans un champ de potentiel artificiel. Ce champ de potentiel est défini comme la combinaison d'un potentiel qui attire le robot vers sa cible et de potentiels qui l'écartent des différents obstacles. Des améliorations de cette méthode ont vu le jour après le résultat satisfaisant qu'elle a donné.

I.8.4.2. Méthode de HUANG: Le principe de cette méthode est d'essayer de joindre la cible en ligne droite (reliant les positions initiale et finale). Si un obstacle intervient en cours du chemin, détecté par les ultrasons placés sur l'avant du robot, il est alors contourné. Des méthodes similaires ont été développées au paravent considérant le robot comme un point matériel et en utilisant d'autres systèmes de perception, mais ayant toujours un principe semblable.

Une adaptation de la méthode de HUANG permettant de prendre en compte les contraintes cinématiques du robot a été testée avec succès.

L'avantage des méthodes utilisant cette approche réside dans leurs efficacités en termes de temps de calcul qui permet leurs utilisations dans des applications temps réel. En

18

Robot Mobile Avec Suivi Visuel De Ligne

Chapitre I : Généralités Sur Les Robots Mobiles

revanche elles présentent l'inconvénient de tomber dans des minima locaux et de générer une trajectoire souvent non optimale.

I.8.5. Approche mixte: L'intérêt de cette approche est de profiter des avantages des deux approches précédentes, à savoir :

* Temps de calcul faible pour l'approche locale.

* Chemin généré optimal pour l'approche globale.

L'idée de cette approche est de générer un chemin optimal, en utilisant une méthode globale, donnant l'allure générale de la trajectoire à suivre.

Ensuite, le robot exécutera cette trajectoire, à l'aide d'un générateur local de trajectoire et de son système de perception, tout en évitant de rentrer en collision avec des obstacles imprévus au moment de la modélisation (changements éventuels de l'environnement, obstacles mobiles) [10].

I.8.6. Approches réactives: Les approches réactives consistent à calculer à chaque pas de temps (après récupération des informations sur l'environnement fournies par les capteurs du système) le contrôle instantané à appliquer sur les actionneurs du système [11]. I.8.6.1. Planification de mouvement partiel: Une dernière approche réactive mérite d'être notée : il s'agit de la planification de mouvement partiel (en anglais : Partial Motion Planning - PMP utilisée. Celle-ci consiste à calculer relativement, en un temps de décision fixe, une trajectoire se rapprochant le plus possible du but. Cette méthode consiste en un algorithme à trois étapes répète à chaque pas de temps :

* Mise à jour du modèle de l'environnement à partir des entrées capteurs du robot.

* Recherche délibérative d'une trajectoire menant à l'état but. Si le but n'a pas été Atteint après un temps de décision fixe, la trajectoire calculée s'en rapprochant le plus est choisie comme trajectoire à suivre.

Enfin, le mouvement planifie au pas de temps précédent est exécuté. Cette approche permet donc d'être réactive aux diverses évolutions de l'environnement tout en étant capable de sortir des impasses non d'détectées à priori. Elle reste sujette à des minima locaux, mais en est néanmoins bien plus robuste que les approches citées précédemment [11].

I.8.6.2. Histogramme de champs de vecteurs: Dans la lignée des approches par champs de potentiels, sont apparus les histogrammes par champs de vecteurs (en anglais : Vector Field Histogram - VFH). Ceux-ci, introduits par Koren et Borenstein sont nés de la combinaison des champs de potentiels et des grilles d'occupation [11] :

19

Chapitre I : Généralités Sur Les Robots Mobiles

Robot Mobile Avec Suivi Visuel De Ligne

Un histogramme basé sur une grille cartésienne de l'environnement est construit et mis à jour au fur et à mesure de la navigation afin de reporter la présence d'obstacles à proximité du robot. Afin de choisir une direction à suivre, un histogramme polaire est construit à partir de la grille d'occupation : en discrétisant les différentes directions possibles autour du robot, l'histogramme polaire est construit en pondérant pour chaque secteur de la discrétisation polaire les cellules traversées de la grille d'occupation contenant des obstacles.

Une fois cet histogramme polaire construit, des »vallées candidates» sont d'exterminés comme les suites de secteurs contigus de l'histogramme polaire libres d'obstacles La direction à prendre par le système est alors déterminée par le milieu de la vallée menant le plus directement au but.

Initialement conçue pour la navigation de robots holonomes (pouvant naviguer dans toutes les directions), cette méthode a été étendue à plusieurs reprises afin de prendre en compte les dimensions du robot (par un espace de configuration implicite) et ses contraintes de vitesse.Plus tard, les VFH ont été combinés à une recherche A* (VFH*) afin de trouver un chemin menant vers le but et d'échapper ainsi aux minima locaux.

Les méthodes VFH disposent néanmoins encore de fortes limitations : Elles ne prennent en compte ni la dynamique du système robotique, ni l'éventuelle présence d'obstacles mobiles ; le mouvement instantané du robot est calculé uniquement à partir des informations sur la position courante des obstacles. Leur vitesse n'est en aucun cas considérée.

I.9. EVITEMENT REACTIF D'OBSTACLES:

Dans cette partie, nous faisons un bref état de l'art des principales méthodes d'évitement réactif d'obstacles afin de mettre en lumière leurs avantages et leurs limites par rapport aux spécificités de notre problématique.

I.9.1. Méthodes analytiques: Même en l'absence d'obstacles, commander un système non holonome pour l'amener d'une configuration de départ a une configuration d'arrivée n'est pas une chose aisée. En effet, il n'existe pas aujourd'hui d'algorithme général permettant de résoudre le problème pour n'importe quel système non holonome.

Des méthodes analytiques sont connues seulement pour certaines classes de systèmes. Pour les autres, on ne dispose que de méthodes numériques. En outre, la présence d'obstacles rend les méthodes analytiques inapplicables à des systèmes non holonomes [9].

20

Robot Mobile Avec Suivi Visuel De Ligne

Chapitre I : Généralités Sur Les Robots Mobiles

1.9.2. Méthode de fenêtre dynamique: Cette technique proposée dans travaille dans l'espace des commandes du robot. La taille du domaine de recherche des vitesses accessibles (c'est-a-dire n'entrainant pas de collisions) est réduite par la prise en compte explicite du modèle cinématique du système. Les commandes envoyées au robot sont le résultat de la maximisation sur ce domaine de recherche d'une fonction cout liée à la configuration finale.

L'utilisation de cette méthode est très intéressante pour un robot se déplaçant rapidement ou pour un robot ayant des capacités d'accélération et de décélération limitées. Elle permet alors de produire un déplacement du robot sur et régulier. Son extension au cadre multi robots est cependant très délicate du fait de son manque de flexibilité [4]. I.10. POURSUITE DE TRAJECTOIRE:

Une fois la trajectoire du robot déterminée dans le contexte de l'évitement d'obstacle ou non, il faut pouvoir la suivre. Le problème de suivi d'une trajectoire de référence pour un robot mobile non-holonome est apparu comme un problème de premier ordre pour la communauté roboticienne dans ces dernières années.

En effet, la forte utilisation des robots mobiles dans les domaines où l'être humain ne peut pas être présent, notamment dans les sites nucléaires à haut risque ou dans le cas de l'exploration spatiale, nécessite la mise en oeuvre de lois de commande autonomes et performantes pour assurer les tâches assignées aux robots. Plusieurs travaux concernant la poursuite de trajectoire ont été développés dans ce contexte. Après une rapide formalisation de ce problème, une liste non exhaustive des différentes commandes disponibles dans la littérature est présentée [4].

Formulation du problème: Une propriété des modèles de robot mobile non-holonome (de type voiture ou uni-cycle) est qu'ils ne sont pas stables par un retour

d'état continu et stationnaire. Ce corollaire est le résultat des travaux de [4].

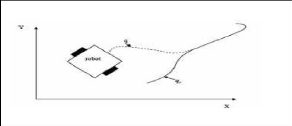
Figure. I.17 : Poursuite de trajectoires admissibles.

21

Robot Mobile Avec Suivi Visuel De Ligne

Chapitre I : Généralités Sur Les Robots Mobiles

I.11. EXEMPLES D'APPLICATIONS:

Aujourd'hui, le marché commercial de la robotique mobile est toujours relativement restreint, mais il existe de nombreuses perspectives de développement qui en feront probablement un domaine important dans le futur.

Les applications des robots peuvent se trouver dans de nombreuses activités "ennuyeuses, salissantes ou dangereuses" (3 D's en anglais pour Dull, Dirty, Dangereuse), mais également pour des applications ludiques ou de service, comme l'assistance aux personnes âgées ou handicapées. Parmi les domaines concernés, citons [12] :

La robotique de service (hôpital, bureaux).

La robotique de loisir (aibo, robot 'compagnon').

La robotique industrielle ou agricole (entrepôts, récolte de productions agricoles, mines).

La robotique en environnement dangereux (spatial, industriel, militaire).

Figure. I.18 : Genghis, développé par Rodney Brooks au MIT au début des années 1990.

A cela, s'ajoute à l'heure actuelle des nombreuses plates-formes conçues essentiellement

Pour les laboratoires de recherche.

La Figure. I.19 montre quelques exemples de robot réels

22

Robot Mobile Avec Suivi Visuel De Ligne

Chapitre I : Généralités Sur Les Robots Mobiles

Figure. I.19: Exemples de robots utilisés dans différentes applications.

I.12. LES TACTIQUE DE NAVIGATION DES ROBOTS MOBILES:

On peut classer ces tactiques en trois groupes, suivant que le robot ne connait rien de son univers de déplacement (robots télémétriques sans mémoires), qu'il le connait totalement (univers connu) ou qu'il le découvre au fur et à mesure de son déplacement (navigation optimisée et interactive avec l'environnement) [8].

I.12.1. Robots télémétriques sans mémoire: Il s'agit de robots qui cherchent à se déplacer dans un univers inconnu pour atteindre un but, en évitant les obstacles à l'aide d'un télémètre à courte ou à longue portée (tactile, ultrasonore ou infrarouge).Pour ce faire, ils sont munis des primitives suivantes:

Aller en ligne droite sur une longueur donnée.

Tourner d'un angle donné.

Viser au télémètre dans une direction donnée.

23

Robot Mobile Avec Suivi Visuel De Ligne

Chapitre I : Généralités Sur Les Robots Mobiles

Certains de ces robots peuvent se repérer par rapport au but, à la fois en direction et en distance Comme ils n'ont pas la mémoire de l'environnement, il n'est pas possible de planifier au départ leur chemin, ni leur donner des informations sur cet environnement.

Néanmoins ils possèdent quelques mots de mémoires qui leur permettent de discriminer l'enchainement des taches à accomplir.

I.12.2. Optimisation de trajectoires dans un univers connu : Dans ce cas, l'univers, connu parfaitement, est modélisé soit par une grille, soit par des polygones. La modélisation par grille a été utilisée dans les premiers travaux de recherche d'un chemin optimal car cette représentation se prête bien à une programmation directe, La robot occupant une case ou étant modélisés par des cases hachurées.

L'univers est ainsi représenté par une matrice, appelée matrice d'adjacence, dont les éléments sont 0 ou 1 suivant que le case correspondante est libre ou occupée par un obstacle .Le déplacement du robot n'est en générale permis que suivant quatre directions perpendiculaires (horizontales et verticale ou huit directions (à 45 ), suivant une direction quelconque.

Dans le modèle des polygones, les obstacles sont modélisés par des polygones dont il suffit de connaitre la position des sommets pour que l'environnement soit parfaitement définit .Dans cette représentation, qui requiert moins de mémoire que la précédente, le chemin est constitué de segments joignant différents sommets de polygones .Ce chemin sera optimal lorsque la somme des couts des arcs constituant le chemin dans le graphe (dont les noeuds sont les sommets des polygones) sera minimale.

I.12.3. Tactiques de navigation optimisées et interactives avec l'environnement:

Ces tactiques s'appliquent aux cas réels fréquents ou l'environnement du robot n'est pas entièrement connu, soit à cause des limites de son organe de vision, soit parce que des obstacles ont pu être ajoutés à l'environnement initiale mémorisé, soit encore par suite de l'imprécision dans la localisation du robot.

Il en résulte une combinaison des tactiques décrites précédemment .Au départ étant donné la connaissance de l'environnement dont dispose le robot, une trajectoire optimale est planifiée et le robot commence à le suivre .En cas de détection imprévue d'un obstacle,

le robot met en action son opérateur de vision pour réactualiser son modèle d'environnement, puis la procédure précédente est réitérée (optimisation, suivi de la trajectoire, vision).

24

Robot Mobile Avec Suivi Visuel De Ligne

Chapitre I : Généralités Sur Les Robots Mobiles

I.13. CONCLUSION:

La perception d'une part et la commande au sens large de l'autre part sont donc les deux thèmes majeurs de recherche pour obtenir un robot mobile parfaitement autonome. Parmi les problématiques liées à la commande, celle de la navigation qui tient un rôle important : elle consiste à déterminer les trajectoires que le robot sera capable de suivre pour lui permettre d'évoluer correctement au milieu d'obstacles.

25

Robot Mobile Avec Suivi Visuel De Ligne

Traitement d'images-Navigation

Chapitre II : Traitement D'images Numérique-Navigation