BIBLIOGRAPHIE
Benoit M., Importance des différents
éléments nutritifs. Pilotage de la fertilisation du verger,
Présentation PPT, 2012 Mar 13, CRAN
Bouvier E. Adapter les apports organiques au sol. CA 84; 2012.
CA Tarn et Garonne (J.-F. Larrieu). Guide fertilisation
raisonnée en arboriculture fruitière. 2010.
Castel B. Le verger cidricole basse-tige normand: vers un
raisonnement de la fertilisation. 1998.
Chantelot E. L'activité biologique des sols
·
Méthodes d'évaluation1. Techn'ITAB; 2003.
Duparque A. Sol et matières organiques. Mémento
pour des notions utiles et contre les idées recues.
AgroTransfert; 2007.
Leclercq B. Guide des matières organiques. ITAB. 2011. 91
p.
Leclercq B. La fertilisation organique en agriculture biologique.
RMT DévAB; 2009
Memento de l'Agronome, 1984, p79
Merwin IA, Stiles WC. Orchard Groundcover Management Impacts on
Apple Tree Growth and Yield,
and Nutrient Availability and Uptake. J Amer Soc Hort Sci. 1994
Mar 1;119(2):209-15.
Référence analyse de sols Deca2014-Cedat et
Deca2011-LCA
Sciences et techniques avicole,Hors série sept 2001
Temen L. FertilisationPK. CA Pays de la Loire;
Trocme, S, and R Gras. 1964. Sol Et Fertilisation En
Arboriculture Fruitière. G.M. Perrin. Bibliothèque
De L'arboriculture Fruitière.
Vaysse P, Soing P, Peyremorte P. L'irrigation des arbres
fruitiers. CTIFL; 1990. 255 p.
1
MORGANE FOURNIER
TESTS STATISTIQUES
ANNEXE 6 - TESTS STATISTIQUES
Etude des variables explicatives - Sur l'ensemble du
réseau
|
azotet
otalen
%ms
|
magnesiumto talen%ms
|
potassiumto talen%ms
|
avantreco lte_n_1
|
sortieh iver_
|
f2plus6 0jours
|
CEC_ca lcium
|
Mg_C EC
|
phenva leuret
|
tauxdem atiereor
|
Nsol_mi n_print
|
Nsol_org a_print
|
Nsol_mi n_ete
|
Nsol_or ga_ete
|
N.fol. ferti
|
Nfoln
_1
|
Mgfo ln_1
|
charg en_1
|
Pluvio
|
Tmoy
|
|
azotetotalen%m
s
|
1.00
|
0.38
|
-0.07
|
0.24
|
-0.07
|
0.75
|
-0.06
|
-0.47
|
-0.32
|
-0.20
|
0.52
|
-0.18
|
0.59
|
-0.04
|
0.47
|
0.64
|
0.17
|
-0.04
|
0.34
|
0.24
|
|
magnesiumtotal en%ms
|
0.38
|
1.00
|
-0.73
|
0.19
|
-0.35
|
0.12
|
0.14
|
-0.02
|
-0.01
|
0.06
|
-0.08
|
-0.14
|
-0.06
|
0.00
|
0.01
|
0.09
|
0.78
|
0.03
|
0.14
|
0.42
|
|
potassiumtotale n%ms
|
-0.07
|
-0.73
|
1.00
|
0.11
|
0.17
|
0.08
|
-0.02
|
-0.39
|
0.12
|
-0.21
|
0.17
|
0.10
|
0.21
|
-0.20
|
0.15
|
-0.01
|
-0.82
|
-0.14
|
-0.18
|
-0.42
|
|
avantrecolte_n_
1
|
0.24
|
0.19
|
0.11
|
1.00
|
-0.22
|
0.49
|
0.91
|
-0.51
|
0.78
|
-0.15
|
-0.06
|
0.08
|
0.17
|
0.43
|
0.31
|
0.26
|
-0.09
|
-0.27
|
-0.35
|
-0.35
|
|
sortiehiver_
|
-0.07
|
-0.35
|
0.17
|
-0.22
|
1.00
|
-0.01
|
-0.27
|
0.36
|
-0.27
|
0.14
|
-0.21
|
-0.13
|
0.06
|
0.10
|
0.00
|
0.20
|
-0.22
|
-0.54
|
-0.23
|
-0.30
|
|
f2plus60jours
|
0.75
|
0.12
|
0.08
|
0.49
|
-0.01
|
1.00
|
0.23
|
-0.53
|
-0.08
|
-0.07
|
0.55
|
-0.15
|
0.82
|
0.15
|
0.67
|
0.65
|
0.10
|
-0.20
|
0.33
|
0.16
|
|
CEC_calcium
|
-0.06
|
0.14
|
-0.02
|
0.91
|
-0.27
|
0.23
|
1.00
|
-0.31
|
0.91
|
-0.13
|
-0.28
|
0.13
|
-0.09
|
0.47
|
0.13
|
0.00
|
-0.05
|
-0.24
|
-0.47
|
-0.41
|
|
Mg_CEC
|
-0.47
|
-0.02
|
-0.39
|
-0.51
|
0.36
|
-0.53
|
-0.31
|
1.00
|
-0.21
|
0.40
|
-0.30
|
-0.35
|
-0.41
|
-0.32
|
-0.66
|
-0.20
|
0.31
|
0.15
|
-0.13
|
0.04
|
|
phenvaleuret
|
-0.32
|
-0.01
|
0.12
|
0.78
|
-0.27
|
-0.08
|
0.91
|
-0.21
|
1.00
|
-0.08
|
-0.36
|
0.08
|
-0.34
|
0.40
|
-0.14
|
-0.19
|
-0.22
|
-0.09
|
-0.59
|
-0.54
|
|
tauxdematiereo
|
-0.20
|
0.06
|
-0.21
|
-0.15
|
0.14
|
-0.07
|
-0.13
|
0.40
|
-0.08
|
1.00
|
-0.15
|
-0.29
|
0.12
|
-0.14
|
-0.39
|
-0.07
|
0.07
|
0.17
|
-0.07
|
0.09
|
|
Nsol_min_print
|
0.52
|
-0.08
|
0.17
|
-0.06
|
-0.21
|
0.55
|
-0.28
|
-0.30
|
-0.36
|
-0.15
|
1.00
|
-0.31
|
0.60
|
-0.17
|
0.23
|
0.53
|
0.17
|
0.44
|
0.45
|
0.22
|
|
Nsol_orga_print
|
-0.18
|
-0.14
|
0.10
|
0.08
|
-0.13
|
-0.15
|
0.13
|
-0.35
|
0.08
|
-0.29
|
-0.31
|
1.00
|
-0.26
|
0.53
|
0.49
|
-0.52
|
-0.18
|
-0.26
|
0.26
|
0.31
|
|
Nsol_min_ete
|
0.59
|
-0.06
|
0.21
|
0.17
|
0.06
|
0.82
|
-0.09
|
-0.41
|
-0.34
|
0.12
|
0.60
|
-0.26
|
1.00
|
-0.15
|
0.51
|
0.73
|
0.02
|
-0.15
|
0.23
|
0.08
|
|
Nsol_orga_ete
|
-0.04
|
0.00
|
-0.20
|
0.43
|
0.10
|
0.15
|
0.47
|
-0.32
|
0.40
|
-0.14
|
-0.17
|
0.53
|
-0.15
|
1.00
|
0.37
|
-0.02
|
-0.01
|
-0.30
|
-0.02
|
-0.06
|
|
N.fol.ferti
|
0.47
|
0.01
|
0.15
|
0.31
|
0.00
|
0.67
|
0.13
|
-0.66
|
-0.14
|
-0.39
|
0.23
|
0.49
|
0.51
|
0.37
|
1.00
|
0.25
|
-0.01
|
-0.33
|
0.49
|
0.28
|
|
Nfoln_1
|
0.64
|
0.09
|
-0.01
|
0.26
|
0.20
|
0.65
|
0.00
|
-0.20
|
-0.19
|
-0.07
|
0.53
|
-0.52
|
0.73
|
-0.02
|
0.25
|
1.00
|
0.13
|
-0.08
|
-0.02
|
-0.23
|
|
Mgfoln_1
|
0.17
|
0.78
|
-0.82
|
-0.09
|
-0.22
|
0.10
|
-0.05
|
0.31
|
-0.22
|
0.07
|
0.17
|
-0.18
|
0.02
|
-0.01
|
-0.01
|
0.13
|
1.00
|
0.14
|
0.33
|
0.56
|
|
chargen_1
|
-0.04
|
0.03
|
-0.14
|
-0.27
|
-0.54
|
-0.20
|
-0.24
|
0.15
|
-0.09
|
0.17
|
0.44
|
-0.26
|
-0.15
|
-0.30
|
-0.33
|
-0.08
|
0.14
|
1.00
|
0.34
|
0.19
|
|
Pluvio
|
0.34
|
0.14
|
-0.18
|
-0.35
|
-0.23
|
0.33
|
-0.47
|
-0.13
|
-0.59
|
-0.07
|
0.45
|
0.26
|
0.23
|
-0.02
|
0.49
|
-0.02
|
0.33
|
0.34
|
1.00
|
0.86
|
|
Tmoy
|
0.24
|
0.42
|
-0.42
|
-0.35
|
-0.30
|
0.16
|
-0.41
|
0.04
|
-0.54
|
0.09
|
0.22
|
0.31
|
0.08
|
-0.06
|
0.28
|
-0.23
|
0.56
|
0.19
|
0.86
|
1.00
|
Figure 1: Coefficient de corrélation
linéaire de Pearson
En rouge les corrélations supérieures
à 0.8 en valeur absolue.
2
MORGANE FOURNIER
TESTS STATISTIQUES
ACP
En observant le graphe représentant les valeurs propres,
nous retenons deux axes.

Figure 2: Graphe représentant les valeurs
propres
En utilisant la règle du coude, nous
déterminons le nombre d'axes à conserver.

Figure 3: Représentation des variables dans le
plan (1;2)
Ce plan représente 42% de l'inertie.
3
MORGANE FOURNIER
TESTS STATISTIQUES
|
Dim.1
|
Dim.2
|
|
azotetotalen%ms
|
0.55
|
0.01
|
|
magnesiumtotalen%ms
|
0.37
|
0.21
|
|
potassiumtotalen%ms
|
0.07
|
0.01
|
|
avantrecolte_n_1
|
0.21
|
0.05
|
|
f2plus60jours
|
0.64
|
0.01
|
|
CEC_calcium
|
0.00
|
0.60
|
|
Mg_CEC
|
0.04
|
0.22
|
|
tauxdematiereor
|
0.22
|
0.06
|
|
Nsol_min_print
|
0.24
|
0.01
|
|
Nsol_orga_print
|
0.05
|
0.40
|
|
Nsol_orga_ete
|
0.01
|
0.67
|
|
N.fol.ferti
|
0.55
|
0.00
|
|
chargen_1
|
0.16
|
0.15
|
|
Pluvio
|
0.10
|
0.36
|
|
Tmoy
|
0.35
|
0.00
|
Figure 4: cos2 associé à chaque variable
sur les axes 1 et 2
Aucun cos2 n'est supérieur à
0.8.
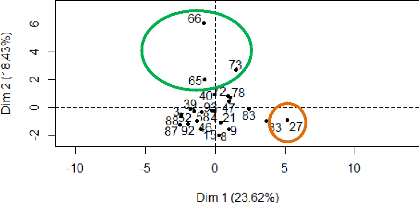
Figure 5: Représentation des individus dans
l'espace (1;2)
Les individus P61 (en vert) et P53 ECO 2014 (en orange)
sont extrêmes.
4
MORGANE FOURNIER
TESTS STATISTIQUES
En enlevant les individus extrêmes
|
azotetota len%ms
|
magnesiumt otalen%ms
|
potassiumt otalen%ms
|
avantrec olte_n_1
|
sortie hiver_
|
f2plus6 0jours
|
CEC_c alcium
|
Mg_CE
C
|
phenva leuret
|
tauxdem atiereor
|
Nsol_mi n_print
|
Nsol_org a_print
|
Nsol_m in_ete
|
Nsol_or ga_ete
|
N.fol .ferti
|
Nfoln
_1
|
Mgfo ln_1
|
charg en_1
|
Pluvio
|
Tmoy
|
|
azotetotalen
|
1.00
|
0.31
|
-0.15
|
0.39
|
-0.05
|
0.76
|
-0.66
|
-0.54
|
-0.71
|
-0.19
|
0.58
|
-0.03
|
0.57
|
0.33
|
0.51
|
0.63
|
0.20
|
-0.03
|
0.41
|
0.29
|
|
magnesiumt otalen%ms
|
0.31
|
1.00
|
-0.82
|
-0.10
|
-0.31
|
-0.01
|
-0.27
|
0.07
|
-0.30
|
0.11
|
-0.05
|
-0.08
|
-0.11
|
0.10
|
-0.04
|
0.04
|
0.82
|
0.10
|
0.23
|
0.52
|
|
potassiumto talen%ms
|
-0.15
|
-0.82
|
1.00
|
0.32
|
0.18
|
0.05
|
0.02
|
-0.46
|
0.27
|
-0.22
|
0.17
|
0.22
|
0.18
|
-0.12
|
0.17
|
-0.03
|
-0.83
|
-0.17
|
-0.21
|
-0.46
|
|
avantrecolte _n_1
|
0.39
|
-0.10
|
0.32
|
1.00
|
0.21
|
0.37
|
-0.02
|
-0.38
|
0.06
|
0.18
|
0.32
|
-0.09
|
0.36
|
0.39
|
0.13
|
0.53
|
-0.29
|
0.04
|
-0.04
|
-0.24
|
|
sortiehiver_
|
-0.05
|
-0.31
|
0.18
|
0.21
|
1.00
|
0.12
|
0.11
|
0.26
|
-0.05
|
0.08
|
-0.28
|
-0.09
|
0.08
|
0.44
|
0.10
|
0.24
|
-0.23
|
-0.69
|
-0.38
|
-0.43
|
|
f2plus60jour
|
0.76
|
-0.01
|
0.05
|
0.37
|
0.12
|
1.00
|
-0.70
|
-0.47
|
-0.74
|
0.03
|
0.70
|
-0.12
|
0.86
|
0.29
|
0.67
|
0.66
|
0.12
|
-0.10
|
0.55
|
0.32
|
|
CEC_calcium
|
-0.66
|
-0.27
|
0.02
|
-0.02
|
0.11
|
-0.70
|
1.00
|
0.61
|
0.87
|
0.39
|
-0.51
|
-0.29
|
-0.63
|
-0.12
|
-0.80
|
-0.34
|
-0.32
|
0.28
|
-0.62
|
-0.56
|
|
Mg_CEC
|
-0.54
|
0.07
|
-0.46
|
-0.38
|
0.26
|
-0.47
|
0.61
|
1.00
|
0.30
|
0.35
|
-0.42
|
-0.32
|
-0.45
|
-0.17
|
-0.62
|
-0.19
|
0.35
|
0.02
|
-0.34
|
-0.11
|
|
phenvaleure
t
|
-0.71
|
-0.30
|
0.27
|
0.06
|
-0.05
|
-0.74
|
0.87
|
0.30
|
1.00
|
0.18
|
-0.38
|
-0.19
|
-0.66
|
-0.14
|
-0.73
|
-0.44
|
-0.43
|
0.31
|
-0.56
|
-0.55
|
|
tauxdematie reor
|
-0.19
|
0.11
|
-0.22
|
0.18
|
0.08
|
0.03
|
0.39
|
0.35
|
0.18
|
1.00
|
-0.20
|
-0.31
|
0.14
|
-0.10
|
-0.35
|
-0.05
|
0.08
|
0.11
|
-0.16
|
0.03
|
|
Nsol_min_pr int
|
0.58
|
-0.05
|
0.17
|
0.32
|
-0.28
|
0.70
|
-0.51
|
-0.42
|
-0.38
|
-0.20
|
1.00
|
-0.31
|
0.62
|
-0.14
|
0.29
|
0.55
|
0.17
|
0.41
|
0.42
|
0.17
|
|
Nsol_orga_p rint
|
-0.03
|
-0.08
|
0.22
|
-0.09
|
-0.09
|
-0.12
|
-0.29
|
-0.32
|
-0.19
|
-0.31
|
-0.31
|
1.00
|
-0.23
|
0.29
|
0.51
|
-0.54
|
-0.23
|
-0.24
|
0.41
|
0.44
|
|
Nsol_min_et
e
|
0.57
|
-0.11
|
0.18
|
0.36
|
0.08
|
0.86
|
-0.63
|
-0.45
|
-0.66
|
0.14
|
0.62
|
-0.23
|
1.00
|
-0.10
|
0.54
|
0.72
|
0.02
|
-0.16
|
0.26
|
0.10
|
|
Nsol_orga_e
te
|
0.33
|
0.10
|
-0.12
|
0.39
|
0.44
|
0.29
|
-0.12
|
-0.17
|
-0.14
|
-0.10
|
-0.14
|
0.29
|
-0.10
|
1.00
|
0.40
|
0.09
|
-0.07
|
-0.25
|
0.34
|
0.18
|
|
N.fol.ferti
|
0.51
|
-0.04
|
0.17
|
0.13
|
0.10
|
0.67
|
-0.80
|
-0.62
|
-0.73
|
-0.35
|
0.29
|
0.51
|
0.54
|
0.40
|
1.00
|
0.25
|
-0.01
|
-0.26
|
0.67
|
0.40
|
|
Nfoln_1
|
0.63
|
0.04
|
-0.03
|
0.53
|
0.24
|
0.66
|
-0.34
|
-0.19
|
-0.44
|
-0.05
|
0.55
|
-0.54
|
0.72
|
0.09
|
0.25
|
1.00
|
0.13
|
-0.06
|
0.00
|
-0.23
|
|
Mgfoln_1
|
0.20
|
0.82
|
-0.83
|
-0.29
|
-0.23
|
0.12
|
-0.32
|
0.35
|
-0.43
|
0.08
|
0.17
|
-0.23
|
0.02
|
-0.07
|
-0.01
|
0.13
|
1.00
|
0.15
|
0.36
|
0.59
|
|
chargen_1
|
-0.03
|
0.10
|
-0.17
|
0.04
|
-0.69
|
-0.10
|
0.28
|
0.02
|
0.31
|
0.11
|
0.41
|
-0.24
|
-0.16
|
-0.25
|
-0.26
|
-0.06
|
0.15
|
1.00
|
0.26
|
0.11
|
|
Pluvio
|
0.41
|
0.23
|
-0.21
|
-0.04
|
-0.38
|
0.55
|
-0.62
|
-0.34
|
-0.56
|
-0.16
|
0.42
|
0.41
|
0.26
|
0.34
|
0.67
|
0.00
|
0.36
|
0.26
|
1.00
|
0.84
|
|
Tmoy
|
0.29
|
0.52
|
-0.46
|
-0.24
|
-0.43
|
0.32
|
-0.56
|
-0.11
|
-0.55
|
0.03
|
0.17
|
0.44
|
0.10
|
0.18
|
0.40
|
-0.23
|
0.59
|
0.11
|
0.84
|
1.00
|
Figure 6: Coefficient de corrélation
linéaire de Pearson. En rouge les corrélations
supérieures à 0.8 en valeur absolue.
MORGANE FOURNIER
TESTS STATISTIQUES
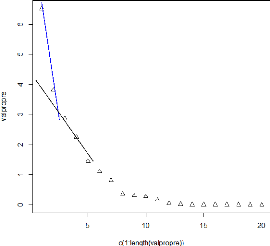
Figure 7: Représentation des valeurs propres.
Nous conservons deux axes.

5
Figure 8: Représentation des variables dans le
plan (1;2)

> colnames(result)
[1] "rendement" "f2plus60jours" "azotetotalen%ms"
[4]
"magnesiumtotalen%ms" "potassiumtotalen%ms" "phenvaleuret"
[7] "tauxdematiereor" "Mg_CEC" "circonf"
[10] "Nfoln_1" "Mgfoln_1" "Pluvio"
[13] "Tmoy" "CEC_calcium"
6
MORGANE FOURNIER
TESTS STATISTIQUES
|
Dim.1
|
Dim.2
|
|
azotetotalen%ms
|
0.64
|
0.01
|
|
magnesiumtotalen%ms
|
0.07
|
0.24
|
|
avantrecolte_n_1
|
0.15
|
0.48
|
|
f2plus60jours
|
0.68
|
0.04
|
|
CEC_calcium
|
0.58
|
0.01
|
|
Mg_CEC
|
0.41
|
0.04
|
|
tauxdematiereor
|
0.06
|
0.31
|
|
Nsol_min_print
|
0.38
|
0.32
|
|
Nsol_orga_print
|
0.04
|
0.55
|
|
Nsol_orga_ete
|
0.10
|
0.11
|
|
N.fol.ferti
|
0.72
|
0.02
|
|
chargen_1
|
0.01
|
0.15
|
|
Pluvio
|
0.26
|
0.14
|
|
Tmoy
|
0.40
|
0.05
|
Figure 9: cos2 des variables sur les axes 1 et 2.
Pas de cos2 supérieur à 0.8

Figure 10: Représentation des individus dans
l'espace (1;2). L'individu 33 peut être considéré
comme extrême. Néanmoins, pour des raisons de nombre de
données complètes, nous choisissons de le conserver. Il sera
à observer lors de modélisations.
ETUDE DES VARIABLES DE SORTIE
L'étude porte sur la table de données
nommées result. La démarche globale est présentée
pour la variable rendement. Pour la modélisation des autres variables,
seul le résultat est présenté.
Rendement
MORGANE FOURNIER
TESTS STATISTIQUES

1) Modèle général
> lm.rdmt0=lm(result$rendement ~
result[,2]+result[,3]+result[,4]+result
[,5]+result[,6]+result[,7]+result[,8]+result[,9]+result[,10]+result[,11]+re
sult[,12]+result[,13])
> summary(lm.rdmt0)
Call:
lm(formula = result$rendement ~ result[, 2] + result[, 3] +
result[, 4] + result[, 5] + result[, 6] + result[, 7] + result[, 8] + result[,
9] + result[, 10] + result[, 11] + result[, 12] +
result[, 13])
Residuals:
1 2 3 4 5 6 7 8 9 10
-2.2255 -3.8259 2.7805 -1.5417 -0.9079 0.8391 2.7859 2.1196
1.5524 2.7849
11 12 13 14 15 16
-1.0097 -0.5783 1.1553 -1.8784 -2.6334 0.5831 Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 3.537087 155.651924 0.023 0.983
result[, 2] -0.010127 0.069857 -0.145 0.894
result[, 3] -16.911461 34.714725 -0.487 0.660
result[, 4] 102.788501 110.757127 0.928 0.422
result[, 5] -1.524060 12.789420 -0.119 0.913
result[, 6] -3.775999 13.997530 -0.270 0.805
result[, 7] 0.317432 3.991177 0.080 0.942
result[, 8] 0.287733 2.514827 0.114 0.916
result[, 9] 1.672080 1.303572 1.283 0.290
result[, 10] 15.538026 18.100377 0.858 0.454
result[, 11] -80.178451 125.680562 -0.638 0.569
result[, 12] -0.007256 0.034003 -0.213 0.845
result[, 13] 0.486012 6.586286 0.074 0.946
Residual standard
error: 4.731 on 3 degrees of freedom Multiple R-squared: 0.8232, Adjusted
R-squared: 0.1158 F-statistic: 1.164 on 12 and 3 DF, p-value: 0.5115
7
2) Sélection de variables sur le modèle
général

> step(lm.rdmt0)
Start: AIC=48.95
result$rendement ~ result[, 2] + result[, 3] + result[, 4] +
result[, 5] + result[, 6] + result[, 7] + result[, 8] + result[,
9] + result[, 10] + result[, 11] + result[, 12] + result[, 13]
Df Sum of Sq RSS AIC
- result[, 13] 1 0.122 67.260 46.976
- result[, 7] 1 0.142 67.279 46.980
- result[, 8] 1 0.293 67.431 47.016
- result[, 5] 1 0.318 67.456 47.022
- result[, 2] 1 0.470 67.608 47.058
- result[, 12] 1 1.019 68.157 47.188
- result[, 6] 1 1.629 68.766 47.330
- result[, 3] 1 5.311 72.449 48.165
<none> 67.138 48.947
- result[, 11] 1 9.108 76.246 48.982
- result[, 10] 1 16.492 83.629 50.461
- result[, 4] 1 19.275 86.413 50.985
- result[, 9] 1 36.821 103.958 53.942
Step: AIC=46.98
result$rendement ~ result[, 2] + result[, 3] + result[, 4] +
result[, 5] + result[, 6] + result[, 7] + result[, 8] + result[, 9] + result[,
10] + result[, 11] + result[, 12]
Df Sum of Sq RSS AIC
- result[, 7] 1 0.294 67.554 45.045
- result[, 8] 1 0.309 67.569 45.049
- result[, 5] 1 0.798 68.058 45.164
- result[, 2] 1 0.844 68.104 45.175
- result[, 12] 1 1.071 68.331 45.228

MORGANE FOURNIER
|
|
|
|
TESTS STATISTIQUES
|
|
- result[,
|
6]
|
1
|
3.729
|
70.989
|
45.839
|
|
|
- result[,
|
3]
|
1
|
5.279
|
72.539
|
46.185
|
|
<none>
|
|
|
|
67.260
|
46.976
|
|
- result[,
|
11]
|
1
|
10.139
|
77.399
|
47.222
|
|
- result[,
|
10]
|
1
|
20.680
|
87.940
|
49.265
|
|
- result[,
|
4]
|
1
|
27.971
|
95.231
|
50.539
|
|
|
|
- result[,
|
9]
|
1
|
39.398
|
106.658
|
52.353
|
|

Step: AIC=45.05
result$rendement ~ result[, 2] + result[, 3] + result[, 4] +
result[, 5] + result[, 6] + result[, 8] + result[, 9] + result[, 10] + result[,
11] + result[, 12]
Df Sum of Sq RSS AIC
- result[, 2] 1 0.654 68.208 43.200
- result[, 5] 1 0.828 68.382 43.240
- result[, 12] 1 1.374 68.928 43.368
- result[, 8] 1 2.279 69.833 43.576
- result[, 6] 1 3.535 71.089 43.861
- result[, 3] 1 8.012 75.566 44.839
<none> 67.554 45.045
- result[, 11] 1 10.773 78.327 45.413
- result[, 10] 1 24.140 91.694 47.934
- result[, 4] 1 29.894 97.448 48.908
- result[, 9] 1 39.799 107.353 50.456
Step: AIC=43.2
result$rendement ~ result[, 3] + result[, 4] + result[, 5] +
result[, 6] + result[, 8] + result[, 9] + result[, 10] + result[, 11] +
result[, 12]
Df Sum of Sq RSS AIC
- result[, 5] 1 0.332 68.540 41.277
- result[, 12] 1 1.512 69.720 41.550
- result[, 8] 1 2.649 70.857 41.809
- result[, 6] 1 2.917 71.125 41.870
- result[, 3] 1 8.528 76.736 43.085
<none> 68.208 43.200
- result[, 11] 1 10.225 78.434 43.435
- result[, 10] 1 23.496 91.705 45.936
- result[, 4] 1 29.439 97.647 46.940
- result[, 9] 1 39.157 107.365 48.458
Step: AIC=41.28
result$rendement ~ result[, 3] + result[, 4] + result[, 6] +
result[, 8] + result[, 9] + result[, 10] + result[, 11] + result[, 12]
Df Sum of Sq RSS AIC
- result[, 12] 1 2.499 71.039 39.850
- result[, 8] 1 2.552 71.092 39.862
- result[, 6] 1 2.749 71.289 39.906
- result[, 3] 1 8.212 76.752 41.088
<none> 68.540 41.277
- result[, 11] 1 20.666 89.206 43.494
- result[, 10] 1 23.199 91.739 43.942
- result[, 4] 1 34.077 102.617 45.735
- result[, 9] 1 43.054 111.595 47.077
Step: AIC=39.85
result$rendement ~ result[, 3] + result[, 4] + result[, 6] +
result[, 8] + result[, 9] + result[, 10] + result[, 11]
Df Sum of Sq RSS AIC
<none> 71.039 39.850
- result[, 8] 1 12.584 83.623 40.460
- result[, 6] 1 18.013 89.052 41.466
- result[, 3] 1 32.330 103.369 43.851
- result[, 4] 1 41.213 112.251 45.170
- result[, 10] 1 60.019 131.058 47.649
- result[, 11] 1 101.630 172.669 52.061
- result[, 9] 1 183.090 254.129 58.244
8
> lm.rdmt1=lm(result$rendement ~
result[,3]+result[,4]+result[,6]+result
[,8]+result[,9]+result[,10]+result[,11])
> Anova(lm.rdmt1)
Anova Table (Type II tests) Response: result$rendement
Sum Sq Df F value Pr(>F)
result[, 3] 32.330 1 3.6409 0.092802 .
result[, 4] 41.213 1 4.6411 0.063347 .
result[, 6] 18.013 1 2.0285 0.192190
result[, 8] 12.584 1 1.4172 0.267993
result[, 9] 183.090 1 20.6185 0.001897 ** result[, 10] 60.019 1
6.7590 0.031628 * result[, 11] 101.630 1 11.4450 0.009598 **
Residuals 71.039 8

4) Modèle final
> lm.rdmt2=lm(result$rendement ~
result[,4]+result[,9]+result[,10]+resul
t[,11])
> summary(lm.rdmt2)
Call:
lm(formula = result$rendement ~ result[, 4] + result[, 9] +
result[,
10] + result[, 11])
Residuals:
Min 1Q Median 3Q Max
-5.4951 -0.9907 -0.2327 2.4529 4.0078 Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -40.6087 9.3066 -4.363 0.001130 **
result[, 4] 111.7790 29.7466 3.758 0.003167 **
result[, 9] 1.5098 0.3264 4.626 0.000734 ***
result[, 10] 5.4161 2.3954 2.261 0.045012 *
result[, 11] -62.1403 21.7008 -2.863 0.015420 *
---
Signif. codes: 0 `***' 0.001 `**' 0.01 `*' 0.05 `.' 0.1 ` ' 1
Residual standard error: 3.091 on 11 degrees of freedom
Multiple R-squared: 0.7232, Adjusted R-squared: 0.6226
F-statistic: 7.186 on 4 and 11 DF, p-value: 0.004253
> Anova(lm.rdmt2)
Anova Table (Type II tests)
Response: result$rendement
Sum Sq Df F value Pr(>F)
result[, 4] 134.881 1 14.1204 0.0031672 ** result[, 9] 204.372 1
21.3954 0.0007338 *** result[, 10] 48.833 1 5.1122 0.0450116 * result[, 11]
78.324 1 8.1996 0.0154199 *
Residuals 105.074 11
9
MORGANE FOURNIER
TESTS STATISTIQUES

Coefficients:
(Intercept) result[, 3] result[, 4] result[, 6] result[, 8]
r
esult[, 9]
13.9253 -24.3931 94.4168 -5.1311 0.8962
1.9218
result[, 10] result[, 11]
17.8719 -78.3522
Call:
lm(formula = result$rendement ~ result[, 3] + result[, 4] +
result[, 6] + result[, 8] + result[, 9] + result[, 10] + result[,
11])
3) Retrait des effets non significatifs sur le
modèle obtenu suite à la sélection de variables
MORGANE FOURNIER
TESTS STATISTIQUES
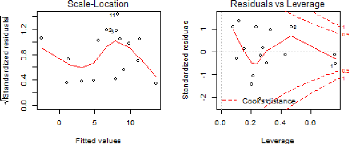
5) Analyse des résidus


Signif. codes: 0 `***' 0.001 `**' 0.01 `*' 0.05 `.' 0.1 ` ' 1
Residual standard error: 0.1963 on 9 degrees of freedom Multiple R-squared:
0.8762, Adjusted R-squared: 0.8212 F-statistic: 15.93 on 4 and 9 DF, p-value:
0.0004085
Call:
lm(formula = result$rdmt_pot ~ result[, 4] + result[, 9] +
result[, 10] + result[, 11])
Residuals:
Min 1Q Median 3Q Max
-0.2568 -0.1323 -0.0125 0.1232 0.3249 Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -3.16036 0.60681 -5.208 0.000558 ***
result[, 4] 13.51904 2.02175 6.687 8.99e-05 ***
result[, 9] 0.09377 0.02140 4.382 0.001767 **
result[, 10] 0.44796 0.15479 2.894 0.017769 *
result[, 11] -8.08538 1.51551 -5.335 0.000472 ***
10
Figure 11: Graphes de diagnostic du modèle
retenu sur le rendement
Rendement potentiel

> colnames(result)
[1] "rdmt_pot" "f2plus60jours" "azotetotalen%ms"
[4]
"magnesiumtotalen%ms" "potassiumtotalen%ms" "phenvaleuret"
[7] "tauxdematiereor" "Mg_CEC" "circonf"
[10] "Nfoln_1" "Mgfoln_1" "Pluvio"
[13] "Tmoy" "CEC_calcium"
> summary(lm.rdmt.pot2)
MORGANE FOURNIER
TESTS STATISTIQUES

> Anova(lm.rdmt.pot2)
Anova Table (Type II tests)
Response: result$rdmt_pot
Sum Sq Df F value Pr(>F)
result[, 4] 1.72231 1 44.713
8.988e-05 *** result[, 9] 0.73953 1 19.199 0.0017668 **
result[, 10] 0.32260 1 8.375 0.0177693 *
result[, 11] 1.09638
1 28.463 0.0004715 *** Residuals 0.34667 9
11
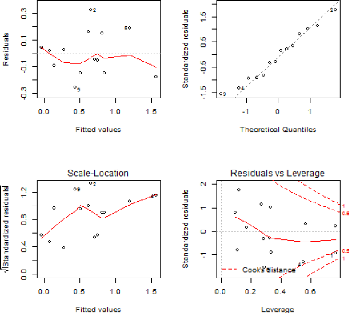
Figure 12: Graphes de diagnostic du modèle
retenu sur le rendement potentiel

> Anova(lm.circonf2)
Anova Table (Type II tests)
Response: result$circonf
Sum Sq Df F value Pr(>F)
result[, 5] 6.870 1 40.7870 2.394e-05 ***
result[, 6] 2.667 1 15.8361 0.001572 **
result[, 7] 0.787 1 4.6731 0.049875 *
result[, 12] 181.788 1
1079.3163 6.765e-14 ***
Residuals 2.190 13
Signif. codes: 0 `***' 0.001 `**' 0.01 `*' 0.05 `.' 0.1 ` ' 1
12
MORGANE FOURNIER
TESTS STATISTIQUES
Circonférence

> colnames(result)
[1] "circonf" "sortiehiver_" "f2plus60jours"
[4] "charge" "azotetotalen%ms" "magnesiumtotalen%ms"
[7] "potassiumtotalen%ms" "phenvaleuret" "tauxdematiereor"
[10] "Mg_CEC" "Pluvio" "circonf_n_1"
[13] "Tmoy" "CEC_calcium"
> summary(lm.circonf2)

Call:
lm(formula = result$circonf ~ result[, 5] + result[, 6] +
result[, 7] + result[, 12])
Coefficients:
Residuals:
Min 1Q Median 3Q Max
-0.92122 -0.17528 0.01895 0.26381 0.53409
Signif. codes: 0 `***' 0.001 `**' 0.01 `*' 0.05 `.' 0.1 ` ' 1
Estimate Std. Error t value Pr(>|t|) (Intercept) 1.08321
1.28219 0.845 0.41349
result[, 5] 2.07111 0.32430 6.386 2.39e-05 ***
result[, 6] -10.64883 2.67595 -3.979 0.00157 **
result[, 7] -0.85969 0.39768 -2.162 0.04988 *
result[, 12] 1.18384 0.03603 32.853 6.76e-14 ***
Residual standard error: 0.4104 on 13 degrees of freedom Multiple
R-squared: 0.9897, Adjusted R-squared: 0.9865 F-statistic: 312.6 on 4 and 13
DF, p-value: 8.953e-13
MORGANE FOURNIER
TESTS STATISTIQUES



Teneur en magnésium foliaire
Un individu a été retiré (P35bis PRO
3ème feuille)
> colnames(result)
[1] "magnesiumtotalen%ms" "azotetotalen%ms"
"potassiumtotalen%ms"
[4] "phenvaleuret" "tauxdematiereor" "Mg_CEC"
[7] "K_CEC" "Nfoln_1" "Mgfoln_1"
[10] "Pluvio" "Tmoy" "CEC_calcium"
[13] "Mg.fol.ferti" "Mg.ferti.sol"
> summary(lm.mg2)
Call:
lm(formula = result[, 1] ~ result[, 3] + result[, 5] +
result[,
10] + result[, 11] + result[, 12])
Residuals:
Min 1Q Median 3Q Max
-0.023201 -0.005240 -0.001115 0.005786 0.031191 Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 7.454e-01 7.415e-02 10.053 2.55e-08 ***
result[,
3] -9.658e-02 1.313e-02 -7.354 1.62e-06 ***
result[, 5] 4.923e-02 5.804e-03 8.481 2.58e-07 ***
result[, 10] 1.780e-04 4.805e-05 3.704 0.001927 **
result[,
11] -2.346e-02 4.647e-03 -5.048 0.000119 *** result[, 12] -2.415e-03 1.932e-04
-12.500 1.14e-09 *** ---
Signif. codes: 0 `***' 0.001 `**' 0.01 `*' 0.05 `.' 0.1 ` ' 1
Residual standard error: 0.01445 on 16 degrees of freedom Multiple R-squared:
0.9286, Adjusted R-squared: 0.9062 F-statistic: 41.59 on 5 and 16 DF, p-value:
1.302e-08
13
Figure 13: Graphes de diagnostic du modèle
retenu sur la circonférence
Etude des variables explicatives

Teneur en potassium foliaire
Deux individus (P14 PRO 2ème et
3ème feuille ont été retirés) >
colnames(result)
[1] "potassiumtotalen%ms" "azotetotalen%ms"
"magnesiumtotalen%ms"
[4] "phenvaleuret" "tauxdematiereor" "Mg_CEC"
[7] "K_CEC" "Pluvio" "Tmoy"
[10] "charge" "CEC_calcium" "K.fol.ferti"
[13] "Ksol_min_print" "Ksol_orga_print"
> summary(lm.k2)
Call:
lm(formula = result[, 1] ~ result[, 2] + result[, 9] +
result[,
11])
Residuals:
Min 1Q Median 3Q Max
-0.30291 -0.13685 0.03071 0.12147 0.32129 Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 4.198737 0.499162 8.412 2.86e-09 ***
result[, 2] -0.279358 0.097827 -2.856 0.00786 **
result[, 9] -0.070663 0.030848 -2.291 0.02944 *
result[, 11] -0.005583 0.001097 -5.090 1.98e-05 ***
14
MORGANE FOURNIER
TESTS STATISTIQUES

> Anova(lm.mg2)
Anova Table (Type II tests) Response: result[, 1]
Sum Sq Df F value Pr(>F)
result[, 3] 0.011287 1 54.080 1.624e-06 *** result[, 5]
0.015013 1 71.931 2.578e-07 *** result[, 10] 0.002863 1 13.718 0.0019268 **
result[, 11] 0.005318 1 25.481 0.0001188 *** result[, 12] 0.032610 1 156.241
1.137e-09 ***
Residuals 0.003339 16
Figure 14: Graphes de diagnostic du modèle
retenu sur la teneur foliaire en magnésium

> colnames(result)
[1] "azotetotalen%ms" "sortiehiver_" "f2plus60jours"
[4]
"magnesiumtotalen%ms" "potassiumtotalen%ms" "phenvaleuret"
[7] "tauxdematiereor" "N.fol.ferti" "Nsol_min_print"
[10] "Nsol_min_ete" "Nsol_orga_print" "Nsol_orga_ete"
[13] "Pluvio" "Tmoy" "charge"
15
MORGANE FOURNIER
TESTS STATISTIQUES
Residual standard error: 0.1699 on 29 degrees of freedom Multiple
R-squared: 0.4923, Adjusted R-squared: 0.4397 F-statistic: 9.372 on 3 and 29
DF, p-value: 0.0001721
> Anova(lm.k2)
Anova Table (Type II tests)
Response: result[, 1]
Sum Sq Df F value Pr(>F)
result[, 2] 0.23543 1 8.1546
0.007857 ** result[, 9] 0.15149 1 5.2472 0.029440 * result[, 11] 0.74790 1
25.9057 1.976e-05 ***
Residuals 0.83724 29
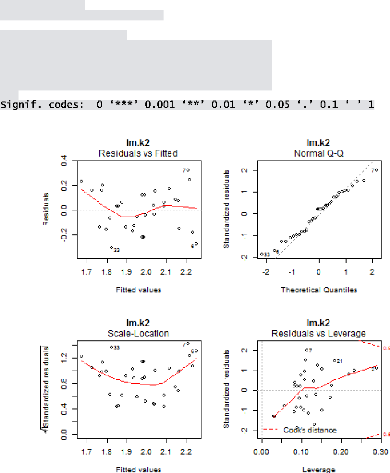
Figure 15: graphes de diagnostic du modèle
retenu pour la teneur en potassium foliaire
Teneur en azote foliaire
16
MORGANE FOURNIER
TESTS STATISTIQUES
> summary(lm.n2)

Call:
lm(formula = result[, 1] ~ result[, 3] + result[, 4])
Coefficients:
Residuals:
Min 1Q Median 3Q Max
-0.45061 -0.16414 0.08583 0.12547 0.26648
Signif. codes: 0 `***' 0.001 `**' 0.01 `*' 0.05 `.' 0.1 ` ' 1
Estimate Std. Error t value Pr(>|t|)
(Intercept) 1.4806805 0.1662514 8.906 9.51e-09 ***
result[, 3] 0.0040996 0.0007488 5.475 1.68e-05 ***
result[, 4] 1.5998887 0.7513809 2.129 0.0447 *
Residual standard error: 0.2024 on 22 degrees of freedom Multiple
R-squared: 0.6367, Adjusted R-squared: 0.6037 F-statistic: 19.28 on 2 and 22
DF, p-value: 1.455e-05

> Anova(lm.n2)
Anova Table (Type II tests)
Response: result[, 1]
Sum Sq Df F value Pr(>F)
result[, 3] 1.22848 1 29.9740
1.682e-05 ***
result[, 4] 0.18582 1 4.5338 0.04467 *
Residuals 0.90166 22
Signif. codes: 0 `***' 0.001 `**' 0.01 `*' 0.05 `.' 0.1 `
' 1
Figure 16: Graphes de diagnostic du modèle
retenu sur la teneur en azote foliaire
1
MORGANE FOURNIER
ETUDE DE LA COMPETITION INTERRANG/POMMIER ET RANG/POMMIER
| 


