III.2.2. RAPPORT DÉTAILLÉ DE LA
REGRESSION
Statistiques de la regression
Coefficient de détermination multiple (R)
0,997967862
Coefficient de détermination R"2 0,995939853
Coefficient de détermination R"2 corrigé
0,995127824
Erreur-type (écart type des erreurs) 3010,216895
Observations 13
III.2.3. ANALYSE DE VARIANCE
Degré de liberté Somme des carrés
Moyenne des carrés F
Valeur
critique de F
Régression (X1 et X2) ESS 2 22227311519 11113655760
1226,48252 1,10334E-12
Résidus (RSS) 10 90614057,55 9061405,755
Total (TSS) 12 22317925577
Coefficients Erreur-type Statistique t
Probabilité
Limite
inférieure
pour seuil de
confiance
=
95%
Limite
supérieure
pour seuil de
confiance
=
95%
Constante Pub
Prix
|
120707,9928
|
11477,88119
|
10,51657451
|
9,9993E-07
|
95133,67986
|
146282,3057
|
|
0,006334374
|
0,000376828
|
16,80973261
|
1,1648E-08
|
0,005494749
|
0,007173999
|
|
-33,87331607
|
10,72322565
|
-3,158873754
|
0,01017827
|
-57,76615166
|
-9,980480483
|

75
III.2.4. ANALYSE DES RÉSIDUS
|
Observation
|
Prévisions Qté
vendue Résidus
|
1 147026,6445 -3588,644453
2 155423,3902 -3140,390185
3 171891,0115 4540,988493
4 178582,4588 2622,541228
5 184980,0295 1825,9705
6 190551,3897 1453,610265
7 196614,6643 1055,335695
8 204952,0267 -1422,026718
9 220708,3685 -3288,368524
10 225590,9056 -1750,905589
11 234111,7548 2172,245199
12 280752,9102 2317,08978
13 286797,4457 -2797,445688

76
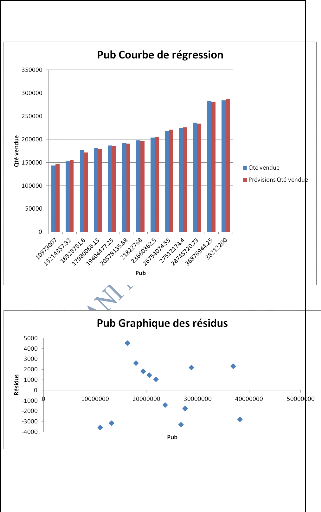
Graphique de la régression
Graphique n°2 : Graphique des résidus

77
Interprétation
Le modèle s'écrit comme suit
t =120707,9928+0,006334X1t-33,87331607X2t Test global du
modèle
Nous utilisons le Test de Ficher SNEDECOR selon les postulants
suivants : Ho : R2=0 : modèle non valide
Ha : R2?0 : modèle valide
Décision : Rejeter Ho si Fcal?Ftab, k-1, n-k. les
résultats montrent que Fcal = 1226,48 alors que Ftab (Ms Excel, Inverse
loi F, O,5 ; 2, 10) donne 0,743491775. Ceci montre que Fcal?Ftab, k-1, n-k.,
nous rejetons Ho au seuil de 5% et concluons que le modèle est
globalement valide et par conséquent, les dépenses publicitaires
expliquent positivement la quantité vendue tandis que le prix influence
négativement celle-ci.
Test individuel du modèle
Test de variable explicative a1
Nous utilisons le test de T-Student selon les hypothèses
suivantes :
Ho : a1=0
Ha : a1?0.
Décision : rejet Ho si Tc?Ttab, n-k. Le modèle
montre que le Tcal est de 16,809 alors que le Ttab (Ms Excel, Loi T-student
inverse, 0,5 ; 10) est de 0,6998. Alors Tcal?Ttab, n-k. Nous rejetons Ho au
seuil de 5% et concluons que la publicité influence significativement et
positivement la quantité vendue.
Test de variable a2
Nous utilisons le test de T-Student selon les hypothèses
suivantes :
Ho : a2=0 Ha : a2?0.

78
Décision : rejet Ho si Tc Ttab, n-k. Les
résultats indiquent que le Tcal est de 3,1588 alors que le Ttab (MS
Excel : Inverse Student, 0,5, 10) est de 0,6998. Nous rejetons Ho au seuil de
5%. Nous concluons que le prix influence significativement et
négativement la quantité vendue.
Test de terme constant a0
Nous utilisons le test de T-Student selon les hypothèses
suivantes :
Ho : a2=0 Ha : a2?0.
Décision : rejet Ho si Tc Ttab, n-k. Les
résultats du modèle indiquent que le Tcal est de 10,5165 tandis
que le Ttab (Ms Excel ; Loi student inverse ; 0,5 ; 10) est de 0,6998. Nous
rejetons Ho au seuil de 5% et concluons que le terme constant influence aussi
significativement et positivement la quantité vendue.
Test de degré de liaison entre les
variables
Ho : R=0 Ha : R?0
Décision : rejet Ho si Tcal Ttab, n-k.
Or, Tcal = R = 0, 9979 = 0, 9979x1, 18033989 = 1, 1156 Ttab, n-k
=0, 6998.
Nous rejetons Ho au seuil de 5% et concluons que le
degré de liaison est différent de 0. Donc, il y a une
corrélation entre les variables explicatives
III.2.5. PROGRAMMATION LINEAIRE III.2.5.1.
Généralité
La programmation linéaire est problème qui
consiste à optimiser (maximiser minimiser) une fonction linéaire
soumise à plusieurs contraintes. Chacune de ces contraintes peut
être une équation linéaire une inégalité
linéaire. La programmation linéaire est la branche de
mathématique consacrée à l'étude de programmation
linéaire.
79

Beaucoup de problèmes concrets qui se posent en micro
ou en macro économie peuvent faire l'objet d'une formulation. Le
programme est dit linéaire car la fonction économique et les
contraintes sont des combinaisons linéaires des variables du premier
degré. Généralement, les contraintes s'énoncent par
les termes suivants : « pas plus que, pas moins que, au plus » et
s'expriment mathématique par un système d'inéquation.
III.2.5.2. La Forme Canonique
Elle se caractérise par des contraintes
présentées sous la forme d'inéquation. De façon
très générale, nous pouvons écrire le
problème de maximisation comme suit :
(1) Max Z = C1X1 + X2 +... + CjXj +.... +
CnXn
Sous contraintes :
2.
3. Et sous les conditions : Xj = 0 ; (j = 1,2 , . n)
Le
programme peut aussi d'écrire comme :
Max =
Ou sous forme matricielle
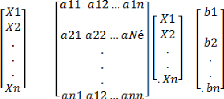
S/C
=
Max Z =
1. On sait que la fonction économique doit être
maximisé (ou minimisée), les signes d'inégalité
dans le système de contraintes prend donc généralement
la
80
Ou encore : Max Z = Cx S/C Ax = B et X = 0
La partie (1) est la fonction « objectif » ou la
fonction économique devant être maximisée. Les contraintes
du groupe (2) s'appellent contraintes fonctionnelles. Celles de la grappe (3)
sont les contraintes de non négativité car on ne peut prendre en
considération des activités de valeur négative, ce qui
n'aurait aucune signification économique.

Max Z =
2.
Le problème de minimisation s'écrira :
Min Z = C1 X1 + C2 X2 +.....+ C3X3 + CnXn
Sous les
contraintes
3. Et sous les conditions : Xj = 0 ; (j = 1,2 , . n)
Min=
Ou sous forme matricielle
Le programme peut aussi d'écrire comme :
S/C
=
et X =
Ou encore : Min Z = Cx S/C Ax = B et X = 0
Avant d'effectuer les calculs permettant de résoudre le
programme linéaire, il peut être souhaitable ou nécessaire
de réaliser certaines transformations.

81
forme canonique = (ou =). Si tel n'est pas le cas, on
harmonise la notation en appliquant la règle suivante : Si a = b, alors
-a = -b, de même, si a =b, alors -a =-b.
Par exemple
2. Il ya deux sens positifs pour une optimisation : soit
maximiser, soit minimiser. Il est intéressant de savoir que Max Z
équivalent à Min (-Z) et que Min Z équivaut à Max
(-Z).
3. Lorsqu'une contrainte s'exprime sous la forme d'une
égalité, deux solutions sont envisageables :
- Ou bien supprimer une variable. En effet,
l'égalité introduit une liaison stricte entre les variables, donc
la connaissance de (n-1) variables entraine la connaissance de la Nième.
La suppression de cette variable doit s'accompagner de l'élimination de
la contrainte d'égalité ;
- Ou bien décomposer la contrainte en deux
inéquations des leurs membres
dans ce cas :
| 


