4. Objectifs et métriques de la simulation
Le but général de ce chapitre est
d'implémenter et d'analyser DVHOP (détaillé en chapitre 2)
un algorithme de localisation sur les réseaux de capteurs sans fil en
particulier:
? Evaluer la précision de la
localisation.
Ces métriques sont évaluées en fonction du
nombre de noeuds ordinaires dans le réseau ainsi que le nombre des
ancres.
Cette formule représente la précision de
localisation de l'algorithme lors d'estimation des distances entre les noeuds
et les ancres. Nous supposons que
Chapitre 4 Implémentation et Evaluation de
DV-Hop
nous connaissons également les vraies positions des
noeuds. La précision d'un noeud Ni est calculée comme suivant:
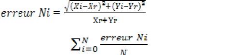
Erreur totale= *100% [13]
Tel que :
Xr, Yr : les positions réelles d'un noeud.
Xi, Yi : les positions d'un noeud trouvées par
DV-hop.
N : le nombre des noeuds ordinaires.
Erreur Ni : l'erreur d'un noeud
Erreur totale: la Moyenne d'erreur de tous les noeuds de
réseau
? La consommation d'énergie.
Ces métriques sont évaluées en fonction
de la taille du réseau
(changement du nombre de noeuds dans le réseau).
5. Version amélioré de DV-hop (Improved
DV-hop )
Le même principe pour la version DV-hop, cependant, on
recalcule les distances entre les noeuds et les ancres, si un noeud
reçoit un hop inférieur à l'ancien hop du même
ancres [14]
6. Résultat de la simulation
6.1 La métrique précision de
localisation
Cette évaluation montre l'efficacité de la phase de
calcule de distance entre chaque noeuds avec tous les autres ancres.
Le but est de savoir la précision de localisation d'un
noeud par rapport à sa position exacte.
La précision de la localisation est évaluée
en fonction de deux paramètres : le nombre de noeuds ordinaires et le
nombre des ancres.
On a utilisé deux versions d'algorithme : la
première est la version basique DV-hop et la
deuxième est la version ameliorée IDV-hop
a. Erreur d'estimation pour la version basique
Scénario 1
Chapitre 4 Implémentation et Evaluation de
DV-Hop
En fonction de densité des noeuds ordinaires, on a obtenu
les résutats suivants avec une topologie constitué en 3 ancres et
5 puis 10 puis 20 noeuds ordinaires
|
Nombre de noeuds
|
5
|
10
|
20
|
|
Erreur (%)
|
54.08
|
50.26
|
34.57
|
Tableau IV. 1: précision de
l'algorithme dvhop en foction de densité de noeuds
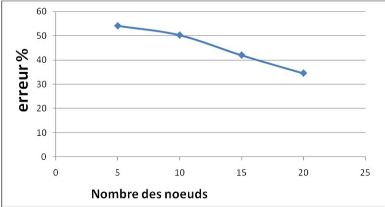
Figure IV. 3: estimation d'erreur de localisation en
fonction de nombre des noeuds Observation et discussion : On remarque
clairement dans le graphe de la
Figure IV.1, que l'errer diminue lorsque le nombre des noeuds
ordinaires augmente. Ceci s'explique par le fait que algorithme DVHOP n'est pas
adapté pour un réseau qui contient un grand nombre de noeuds.
Scénario 2
En fonction de densité des ancres, on a obtenu les
résutats suivants avec une topologie constituée en 5 noeuds et 3
ancres puis 4, 5, 6 et 7 ancres
|
Nombre d'ancres
|
3
|
4
|
5
|
6
|
7
|
|
Erreur (%)
|
54.08
|
40.1
|
36.71
|
30
|
24.73
|
Tableau IV. 2: précision de
l'algorithme dvhop en foction de densité d'ancres
Chapitre 4 Implémentation et Evaluation de
DV-Hop
3 4 5 6 7
60
50
erreur %
40
30
20
10
0
Nombre des ancres
Figure IV. 4: estimation d'erreur de localisation en
fonction de nombre des ancres
Observation et discussion :
On remarque clairement dans le graphe de la Figure IV.2, que
l'erreur diminue lorsque le nombre des ancres augmente car dans
la
phase de multilateration, la zone d'intersection des cercles
qui
representent les zones de couvertures, va dimunuer et les
coordonnées X et Y sont inclus dans cette zone, donc l'erreur va
dimunuer.
b. Erreur d'estimation pour la version ameliorée
Scénario 1
En fonction de densité des noeuds ordinaires, on a obtenu
les résutats suivants avec une topologie constituée de 3 ancres
et 5 puis 10 puis 20 noeuds ordinaires
|
Nombre de noeuds
|
5
|
10
|
20
|
|
Erreur (%)
|
30.22
|
27.31
|
23.76
|
Tableau IV. 3: Précision de
l'algorithme dvhop en foction de densité de noeuds
Chapitre 4 Implémentation et Evaluation de
DV-Hop
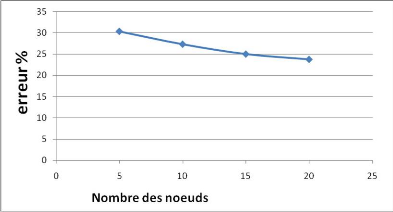
Figure IV. 5 : estimation d'erreur de localisation en
fonction de nombre de noeuds
Observation et discussion : On remarque
clairement dans le graphe de la Figure IV.3, que l'errer diminue lorsque le
nombre des noueds ordinaires augmente. Ceci s'explique par le fait que
algorithme DVHOP n'est pas adapté pour un réseau qui contient un
grand nombre de noeuds.
Scénario 2
En fonction de la densité des ancres, on a obtenu les
résutats suivants avec une topologie constituée en 5 noeuds et 3
ancres puis 4, 5, 6 et 7 ancres.
|
Nombre d'ancres
|
3
|
4
|
5
|
6
|
7
|
|
Erreur (%)
|
30.22
|
27.33
|
24.45
|
23.25
|
22.15
|
Tableau IV. 4: précision de
l'algorithme IDV-hop en foction de la densité d'ancres
Chapitre 4 Implémentation et Evaluation de
DV-Hop
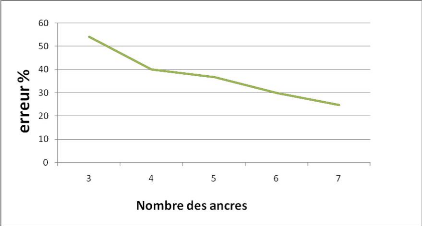
Figure IV. 6: estimation d'erreur de localisation en
fonction de nombre des ancres
Observation et discussion : On remarque
clairement dans le graphe de la Figure IV.4, que l'erreur diminue lorsque le
nombre des ancres augmente, car dans la phase de multilateration la zone
d'intersection des cercles qui representent les zones de couvertures va
dimunuer et les coordonnées X et Y sont inclues dans cette zone, donc
l'erreur va dimunuer
| 


