3. Estimation des coordonnées
DVHOP est un algorithme de localisation. Son but est de
permettre aux capteurs de trouver leurs positions à l'aide des positions
connues de quelques capteurs spécifiques appelés (ancres).
En plus, la localisation par moyens propres est donc
indispensable. Elle se fait en deux étapes : premièrement
l'estimation de la distance aux autres noeuds, et deuxièmement la
multilatiration.
Chapitre 4 Implémentation et Evaluation de
DV-Hop
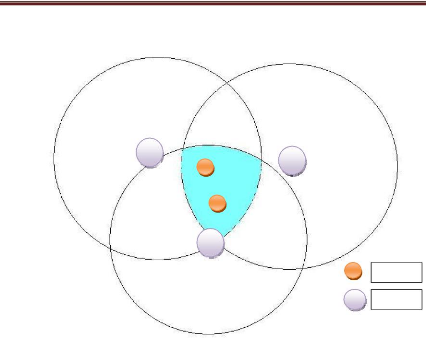
Noeud
Ancre
Figure IV. 2: Figure représentant le
modèle réel.
Figure IV.2 illustre un modèle de réseaux des
capteurs sans fil en utilisant la méthode de multilatiration pour
estimer les positions des noeuds, les boules violées représentent
les ancres (leur position est connue) et les oranges représentent les
noeuds (leur position est inconnue).
Les cercles représetnent les zones de couvertures des
ancres, pour que l'erreur d'estimation soit minimale, il faut placer les noeuds
dans la zone d'intersection des cercles (zone bleu)
A- Estimation de la distance
L'estimation de distance peut se faire sur base de
différents indicateurs :
? Le temps de propagation d'une onde.
? La puissance du signal à la réception.
? Le taux d'erreurs corrigées lors des transmissions.
? Le nombre de saut.
Chapitre 4 Implémentation et Evaluation de
DV-Hop
B- Multilatération
La Multilatération est une méthode relativement
simple et intuitive, en utilisant plus que trois points de
référence (ancres). La position d'un noeud est calculée en
connaissant les positions d'un certains ancres et les distances estimées
de ce noeuds aux différents ancres.nous formons le système
suivant :
Soit une cible a dont on veut trouver la position Xa, et soit m
ancres i dont
nous connaissons les positions xi, 1 < i <m,
Nous
supposons que nous connaissons aussi une estimation des distances Dai 1
< i <m entre chaque ancre i et le noeud a.
Nous pouvons alors poser :
(x11 - xa1)2 + (x12 - xa2)2 + . . . + (x1p
- xap)2 = d21a ...
(xm1 - xa1)2 + (xm2 - xa2)2 + . . . + (x1p
- xap)2 = d2 ma
Le système peut être linéaire en soustrayant
la dernière équation des m - 1 équations
précédentes.
x2 11 - x2 m1 - 2(x11 - xm1)xa1
+x2 12 - x2 m2 - 2(x12 - xm2)xa2
+. . .
+x21p - x2 mp - 2(x1p - xmp)xap = d2 1a - d2
ma
...
...
x2(m-1)1 - x2 m1 - 2(x(m-1)1 - xm1)xa1
+x2(m-1)2 - x2 m2 - 2(x(m-1)2 - xm2)xa2
+. . .
+x2(m-1)p - x2 mp - 2(x(m-1)p - xmp)xap =
d2(m-1)a - d2 ma
En réordonnant les termes, nous obtenons un système
d'équations linéaires de la forme Ax = b où :
2(x11 - xm1) . . . 2(x1p - xmp)
Chapitre 4 Implémentation et Evaluation de
DV-Hop
...
2(x(m-1)1 - xm1) . . . 2(x(m-1)p - xmp)
x2 11 - x2 m1 + . . . + x2 1p - x2 mp + d2 ma - d2 1a
B= ...
...
x2 (m-1)1 - x2 m1 + . . . + x2 (m-1)p - x2 mp + d2 ma - d2
(m-1)a
Comme nous avons des erreurs dans les estimations de
distances, nous ne pouvons pas trouver de solution exacte à ce
système d'équationsEt donc :
Xa = = (ATA)
-1ATb.
xa1
xa2
Où xa=
C'est-à-dire notre estimation de la position du noeud
a.
xap
Le processus peut être recommencé avec tous les
noeuds inconnus du réseau. Nous obtenons ainsi les positions de tous les
noeuds dans le réseau. Cette méthode sera
implémentée par Delphi.
| 


