Memoire Online - Modélisation et couverture des comptes courants postaux

Cette étude sur la modélisation et la couverture des comptes courants a consisté à explorer les différentes facettes que revêt la gestion actif-passif du point de vue d'une banque de détail.

Le premier enjeu à relever était de proposer des scénarios d'évolution de l'encours global des comptes à vue. La description de la dynamique future de ce passif bancaire, sans maturité contractuellement définie, est essentielle dans l'optique d'équilibrer le bilan de l'établissement à chaque date. Les articles académiques traitant de ce sujet ne proposant, de notre point de vue, que des modélisations macroéconomiques, superficielles et ne tenant pas suffisamment compte des spécificités de cette variable, nous avons défini un cadre théorique bien plus fin en y intégrant simultanément des aspects macroéconomiques, comportementaux et démographiques. Le modèle probabiliste construit, de type markovien, est bâti sur des facteurs variés, tels que l'inflation, l'évolution future de la pyramide des âges, les taux de mortalité, la structure par âge de la base de clientèle ou encore les caractéristiques «financières» des clients. Il repose sur une ventilation de la clientèle par strates et par âges et permet de générer des trajectoires d'évolution de l'encours global en reproduisant les mouvements sur les comptes courants de chacun des clients de la banque de détail.

L'utilisation de l'outil informatique et de nombreuses simulations de type Monte-Carlo nous ont permis d'établir ou de retrouver de nombreux faits stylisés et de réaliser l'importance cruciale de certains paramètres du modèle.

En particulier, il s'est avéré que la modélisation retenue pour l'inflation conditionne fortement la dispersion de l'encours à une date future donnée : une inflation aléatoire et plus volatile élargit les intervalles de confiance pour la valeur de l'encours.

Le degré de mobilité des clients, qui caractérise leur propension à changer facilement d'état et à sortir plus facilement, est un déterminant essentiel de la volatilité de l'encours. Ainsi, plus la base de clientèle est mobile, plus notre pouvoir prévisionnel sur l'évolution de l'encours, aux pas de temps suivants, est dégradé. Enfin, les taux de sortie des clients modifient de manière importante la durée de vie des dépôts, dans une vision «mort du bilan» de vieillissement du stock existant lorsque la banque arrête toute commercialisation de produits.

La démographie actuelle de la clientèle est quant à elle un facteur déterminant de la croissance de l'encours sur le court-moyen terme. Nous y mettons en évidence que, dans le cadre de notre modèle, l'arrivée de la génération du baby-boom dans des âges avancés est susceptible d'entraîner, dans un futur proche, une surperformance de l'augmentation de l'encours par rapport à ce que l'on pourrait s'attendre a priori (car les personnes âgées détiennent en moyenne plus de liquidités). Nous avons aussi pu vérifier qu'une banque, typiquement en ligne, qui se caractérise par une clientèle très jeune, connaît une surperformance sensible de la croissance de son encours. Cela est lié au vieillissement de sa clientèle et à l'augmentation de l'effectif de cette dernière. À l'inverse, une base de clientèle initialement âgée peut entraîner une stagnation de l'encours, voire une décroissance de celui-ci, sur le court-moyen terme en raison de la perte prochaine des clients les plus aisés.

Afin d'inscrire ce modèle «innovant» d'évolution de l'encours dans le cadre de la gestion du bilan bancaire, il s'est agi ensuite de proposer des stratégies d'investissement de l'encours bancaire que nous avions modélisé. L'enjeu était d'illustrer, dans le cadre du modèle construit, le risque de liquidité dont doivent tenir compte les banques de détail dans leur allocation de capital entre les supports de taux court-terme et long-terme. Nous y avons donc intégré un modèle financier classique sur les taux. En nous appuyant sur le modèle de Hull et White, nous avons d'abord diffusé les taux spots et les courbes zéros-coupons associées à différentes échéances. Nous avons ensuite analysé les performances de stratégies financières

simples, consistant à placer à court terme une proportion constante fixée de l'encours et à placer le résiduel à long terme sur des obligations à cinq ans, et ce à chaque date. Nous avons retenu le concept de marge nette dégagée par l'établissement sur une période donnée, définie comme la rémunération qu'il perçoit à chaque date, au titre de ses placements passés sur les marchés. En simulant la marge générée sous différentes stratégies, nous avons vu que la banque de détail doit réaliser un arbitrage entre un critère de risque et un critère de lissage de la rémunération dans le temps dans le choix de sa stratégie «optimale». Ainsi, plus l'établissement place une part importante de son bilan à long terme, plus il diminue la volatilité de sa marge mais plus il s'expose à un fort risque de liquidité : en cas de situation de stress, caractérisée par une sortie subite et massive de clients, éventuellement couplée à une hausse des taux, l'établissement est obligé de liquider dans l'urgence, voire à perte, ses actifs longs. A contrario, plus la banque place à court terme, moins elle est exposée à ce risque, mais plus sa marge est tributaire des mouvements de la courbe des taux et a un caractère volatile. Dès lors, dans le premier cas, l'établissement s'affranchit, en partie, des effets de cycle (notamment des périodes où les taux chutent) alors que dans le second, sa rémunération les suit certes très fortement, mais l'optique d'investissement est bien plus prudente du point de vue du risque de liquidité. La définition de l'optimalité de la politique de placement doit donc s'apprécier au regard de la politique de risque souscrite par la banque. Néanmoins, nous y avons établi que la structure par âge actuelle de la clientèle de l'établissement est un facteur influençant le choix de la stratégie. Ainsi, à volatilité de marge donnée (correspondant donc à une certaine allocation entre placements court-terme et long-terme), une banque présentant une clientèle jeune (respectivement âgée) s'expose à un risque de liquidité inférieur (respectivement supérieur) sur le scénario catastrophe généré. La raison à ce résultat est le différentiel de croissance dans l'encours de ces banques. Finalement, dans le cadre de notre modélisation, la banque de détail va donc choisir d'investir une proportion d'autant plus importante de l'encours global sur le long terme que sa clientèle est jeune.

Des pistes d'amélioration de cette étude peuvent être suggérées. Une démarche de calibration du modèle sur les données historiques d'une banque de détail permettrait, notamment, d'inscrire celui-ci dans un cadre plus concret et de confronter ses capacités prédictives à la réalité. Cette calibration se heurte toutefois à la difficulté pratique de collecte des données : le modèle construit présuppose, en effet, que la banque ait compartimenté sa clientèle en strates, mais aussi et surtout qu'elle dispose d'un suivi individuel suffisamment long de chaque client, ceci afin d'estimer correctement les paramètres, tels que les taux de transition. Par ailleurs, nous avons été amenés à poser des hypothèses théoriques a priori pour de nombreux éléments du modèle, essentiellement dans un souci de ne pas trop le complexifier. Enfin, il faut garder à l'esprit que notre modèle est adapté pour capter des tendances, mais qu'il ne peut, bien évidemment, prétendre à une exhaustivité descriptive de la dynamique des encours bancaires. Ces derniers sont assujettis à de très nombreuses variables économiques, démographiques, financières et même comportementales que notre modèle ne peut reproduire dans leur intégralité. Enfin, le processus de choix de la stratégie financière, confiné dans notre travail au choix d'une proportion entre deux alternatives d'investissement (court terme et obligations à cinq ans), pourrait être enrichi d'une dimension, en intégrant également le choix de l'échéance des placements à long terme que l'on souhaite effectuer. Cette piste de recherche supplémentaire aurait l'avantage de tenir compte de la forme de la courbe des taux à chaque date afin d'optimiser la rémunération perçue.

L'objet de ce point d'annexe est de mener une discussion brève sur l'inférence statistique à laquelle nous pouvons prétendre sur la forme de l'évolution de l'encours At des dépôts de la banque, à partir de l'observation de sa trajectoire passée.

Soit T > 0. On considère le processus des encours _(At)tE[0,T] observé sur l'intervalle [0, T] à intervalles de temps discrets aux points 0, 6, 26, ..., n6 =T. Le résultat de l'observation est un vecteur _A(T ),ä = (A0, Aä, _A2ä, ..., AT).

avec u > 0 constant et o- constant et _(Wt)tE[0,T] un mouvement brownien standard.

Si le processus suivait une telle dynamique, At suivrait à chaque date une loi log-normale

En particulier, l'espérance et la variance de la variable At croîtraient exponentiellement, respectivement selon

Une question naturelle vient à l'esprit : l'observation de la trajectoire historique permet-elle d'infirmer l'hypothèse _Hu,ó d'évolution de At selon l'EDS (*) ?

La réponse est (malheureusement) négative. Dans la mesure où nous disposons de la valeur de At à des dates discrètes (pas de temps mensuel), il est impossible d'infirmer l'hypothèse Hu,ó pour la simple raison que le support de la loi de A (T),ä est (R+)ⁿ+¹ tout entier!

On peut d'ailleurs préciser ici que même si l'on observait le processus At continûment, c'est-à-dire même si l'on disposait de la donnée A^(T) = (At,t E [0,T]), on ne pourrait pas pour autant se prononcer sur l'existence d'une tendance !

La raison tient en un argument mathématique sur les lois de probabilités des processus que nous développons brièvement ci-dessous³².

Si l'on observe une trajectoire Z sur [0, T], dire si Z a été tiré selon P ou Q à coup sûr (risques de première et de deuxième espèces nuls) signifie qu'il existe un ensemble de trajectoires A tel que P(A)=0 et Q(A)=1 soit que PIQ.

De même, on ne peut pas distinguer P^Tó², u1 et P^Tó², u2 si les deux mesures sont équivalentes,

soit P^Tó², u1 << P^Tó², u2 et P^Tó², u2 << P^Tó², u1. Or c'est une conséquence immédiate du théorème de Girsanov que pour u1 #u2, P^Tó², u1 ^ P^Tó², u2.

³²Rappel : soient P1 et P2 deux mesures de probabilités définies sur un espace (S2, T). On dit que :

Autrement dit, pour T fini, on «peut supposer» u = ó2 2 ! Pour pouvoir se prononcer, il faudrait l'observation de la trajectoire complète, c'est-à-dire T = oc, dans la mesure où

Ces considérations invitent donc à la prudence quant à toute interprétation trop hâtive suite à une observation limitée du processus étudié.

Toutefois, en dépit de cette remarque, on peut tout de même se demander s'il est «raisonnable» d'accepter l'hypothèse _Hu,ó.Pour ce faire, on peut par exemple remarquer que sous _Hu,ó,on a

c'est-à-dire ln(Ät)-ln(Ät_1)=m(t) où les _{{m(t)}tE{ä,2ä,...,nä}}sont des variables gaussiennes

indépendantes identiquement distribuées d'espérance u- ó2 2 et de variance ó². Une approche peut ainsi consister à tracer les valeurs prises par les variables m(t) au cours du temps. Voici ce que l'on obtient à titre d'exemple sur les données historiques mensuelles de La Banque Postale de janvier 1994 à décembre 2010.

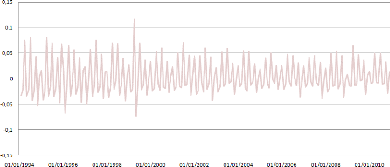
À première vue, ce graphe ne suggère pas la stationnarité des variables (les fluctuations sont quasiment deux fois plus importantes au début de la période qu'à la fin).

Cette annexe détaille les étapes de calcul permettant d'obtenir les formules annoncées du modèle de Hull et White, numérotées de 1 à 6 dans le rapport.

Formule (1) : En posant Yt, = rt,e^at', la formule d'Itô donne dYt, = drt,e^at' + art,e^at'dt^'

((b_t, - art') dt^' + ódWt,) ^eat' + aYt,dt^' e^at'bt0dt^' + óe^at'dWt,

donc pour T^' >t^', on a YT0 = Yt' + _f e^asb_sds + ó _f e^asdW_s et donc

Formule (2) : Par définition, I(t^', T^')= Jr_udu d'où en tenant compte de la formule (1)

rt0

I(t^',T^') = (1 - e-

a(T'-t')) + _Z
T0(_f T0 e-a(u-s)du) b_sds + ó _1T0 (rT 0e-a(u-s)du) d W_s

rt0

I(t^',T^') = (1 - e-

T0 1 - e a(T'-s) ó fT0

a(T'-t')) +Z b_sds + (1 - e-a(T0-s)) dWs

a a

L'indépendance des accroissements du brownien et l'isométrie d'Itô sur les intégrales stochastiques prouvent alors que la loi conditionnelle de I(t^', T^') sachant Ft, est la gaussienne

rt,

(1 - e-

T01 - e a(T^'-s)_ó2_L

T0 2

a(T'-e)) + b_sds , 2 (1 - _e-a(T -s)) ds!

f_t,

â a

f(0,T^') = r0e^-^aT0 +

_/'T^'

J 0 e

-a(T'-s)bsds - 2a2 (1 - 2e-aT0 + e-2aT')

?f(0,T^')
?T'

ar0e

aT0 + bT0 + _r (-a)e^-^a(T'-s)b_sds - 2~2 (2ae-aT' - 2ae-2aT0~

On retrouve exactement l'intégrande dans la formule donnant rT 0 figurant ci-dessus. Par conséquent

rT 0 = rte

~T y^'(s)ds + ó fT0 e-a(T'-s)dWs _t' '
_fT0

a(T'-t') + y(T^') - y(t^') + ó e-a(T'-s)dWs

_t'

_fT0

a(T'-t') + ã(T^') - ã(t^')e^-^a(T'-t') + ó ^e-a(T'-s)d Ws

_t'

-ln(B(0,t^')) + ln(B(0,T^')) = m(0, t^') - m(0,T^') - 2 (V (0, t^') - V (0, T^'))

rt'

m(t^', T^') = (1 - e-

rt'

m(t^', T^') = a (1 - e-

a(T'-t')) + f T { (u) - ã(t^')e^-^a(u-t')} du

_t'

a(T'-t')) +_J'^T ã(u (u)du i(')1 - _e-â(T -t^')

-- t

m(0,p) = (1 - e-

_fP

ap) 1--

+ ^J y(u)du -- y(0) âe

rt'

m(t^',T^') = (1 - e-

a(T'-t')) + _f ã(u)du - f

ã(u)du - ã(t')1 a

m(t^',T^') = rt'P(t^',T^') + m(0,T^') - m(0,t^') - ã(t^')P(t^',T^')

Formule (6) : La relation ^{B(t',T')=e-m(t',T')+12V(t',T')} couplée à la formule (5) donne

B(t^',T^') = B(0,T')e

B(0, t )

1 1

2 (V (0,T^') - V (0,t^')) - P(t^',T^') (rt' - ã(t^')) + ₂V (t^',T^')

en notant S(t^',T^')=-₂ (V (0,T ') - V (0,t^')) + ₂V (t^',T^') + P(t^',T^')ã(t^').

Partant de l'expression V (t^', T^') = peut écrire

ó2 fT' - t^' + 2e-a(T'-t') - 1 _e-2a(T'-t') 3 on

COL a 2a 2a1^,

2at'l

V (0,T^') - V (0,t^') =

+ 2 (e

aT'

e at^'

2aT'

-t'

[_T'

a \ / 2a \ /]

V (0,T^') - V (0,t^') = V (t^',T^') +

ó²

a2 2 a(T'-t') + 12ae 2a(T'-t') + 32a+

2 -

V (0,T^') - V (0,t^') = V (t^',T^') +

₂

ó²

a a (1 - e-a(T'-t')) - 1 (1 - (T

e-2a'-t')) +

2 / /

V (0, T^') - V (0,t^') = V (t^',T^') + a2 [:(1 - e-at'/ (1 - e -a(T'-t')) - 2a (1 - e-2at') (1 - e-2a(T'-t'))J

S(t^', T^') = P(t^', T^') (f(0,t^') + 2a2 (1 - 2e-at' + ^e-2a1) + ^2a2 h-2 (1 - e-at) P(t^' T^')+

S(t^',T^') = P(t^',T^')f(0,t^') + _2a2 hP(t^', T') (1 - 2e-at' + e-2at' - 2 (1 - e-at')) + 2a (11 - e-2at') (1 - e-2a(T'-t'))J

S(t^', T^') = P(t^', T^')f(0, t^') + 2a2 (1 e-2at') [-P(t^',T^') + 2a (1 - e 2a(T'-t'))J

B(t^', T^') = B~ô_' ~ exp ^S (f(0, t^') - rt') P(t^', T^') - 4a (1 - e ^2at') P(t',T')2}

Modélisation et couverture des comptes courants postaux

Conclusion