4.3 Un modèle pour l'inflation
La régression précédente nous incite
à intégrer l'inflation dans le modèle mathématique
de dynamique des encours que nous allons construire. Il nous faut donc adopter
un modèle pour cette grandeur économique. Nous allons commencer
par définir les notations et le vocabulaire que nous utiliserons dans
cette étude. Dorénavant, nous appellerons inflation
mensuelle, ou plus simplement inflation, sur la période
[t - 1, t] (où t N"
décompte le temps en mois) le taux itt d'augmentation des
prix sur cette période. Cette variable capture localement, à une
échelle mensuelle, la dynamique d'évolution des prix. Nous
définissons le niveau d'inflation par ilt = (1 +
lrt)llt_1 : il mesure la tendance au cours du temps de
l'évolution des prix. En particulier, le niveau d'inflation est
défini à multiplication par une constante près. Pour y
remédier, on peut donc fixer son niveau à une certaine date de
manière arbitraire (en général à 100). Il
s'identifie alors à ce qui est appelé Indice des Prix
à la Consommation (IPC). C'est sur cette dernière variable,
publiée par l'Institut National de la Statistique et des
Études Économiques (INSEE), que nous avons effectué
la dernière régression.
Nous adopterons pour l'inflation un modèle similaire
à celui proposé par Vasièek en 1977 pour la dynamique du
taux spot sans risque. Nous considérons ainsi que l'inflation men-
suelle 7rt suit sur un espace (S2, IF,
P) - où P désigne la probabilité historique - une
équation différentielle stochastique d'Ornstein-Uhlenbeck,
selon
d7rt = a(b - 7rt)dt
+ QdWt , t E R+
avec Wt un mouvement brownien standard unidimensionnel,
dont la filtration naturelle sera dorénavant notée Gt
=Q(Wt, 0<u<t).
Le modèle est spécifié par trois
paramètres : a, b et la volatilité a
ER*+. Il s'agit d'un modèle dit de
retour à la moyenne car le processus 7rt oscille autour de
b. Ainsi, a > 0 est un paramètre d'échelle
qui mesure la vitesse de rappel vers b du processus 7rt.
Cette équation différentielle stochastique se
résout explicitement par
t
7rt = 7r0e-at + b
(1 - e-at) + a
J
e-a(t-s)dWs (1)
0
On a même plus généralement pour
0<t1 <t2
t2
\ f
7rt2 =
7rt1e-a(t2-t1) + b
(1 - e-a(t2-t1)/ + a J
e--a(t2-s)dWs (2)
t1
Par le théorème d'isométrie des
intégrales stochastiques, l'intégrale de Wiener du membre de
2
droite dans (1) est une variable gaussienne centrée de
variance Q2 Ret,
e-2a(t-s)ds = 2a (1
- e-2at)
Par conséquent
2 1 7rt N
(7r0e-at + b (1 - e-at)
2a (1 - e-2at))
|
En particulier, EP(7rt) =
7r0e-at + b (1 -
e-at) et VP(7rt) =
|
0.2 2a
|
(1 - e-2at), qui convergent
|
22
0.2
respectivement lorsque t ? +oo vers b et
7.
2a
Par ailleurs, l'indépendance des accroissements du
brownien, combinée à l'expression (2),
permet d'affirmer que la loi conditionnelle de 7rt
sachant 7rt-1 est la gaussienne
2
N (7rt-1e-a + b
(1 - e-a) , 2a (1 -
e-2a)/11
Cette remarque est de première importance pour la
simulation informatique de l'inflation. En effet, même si sa dynamique
est décrite ici de manière continue, nous la considèrerons
uniquement à des instants discrets (t=0, 1,
2, ...). Ainsi, partant de 7r0, il suffira de
générer des lois normales successives, dont les paramètres
dépendent du niveau précédent de l'inflation, pour obtenir
de proche en proche une trajectoire de cette dernière.
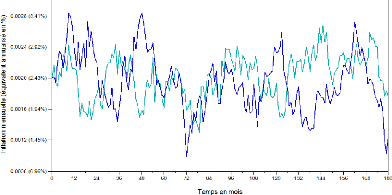
À titre illustratif, nous avons simulé puis
tracé ci-après deux trajectoires pour un quadruplet de
paramètres identiques (a, b, a, 7r0) = (0.2,
0.002, 0.0002, 0.002) sur un
horizon h = 180 mois, correspondant à 15 ans. Sachant que
l'objectif annoncé de la Banque Centrale Européenne est
une inflation annuelle à 2%, le choix des paramètres s'est
effectué a priori en cherchant à revenir en moyenne vers
une valeur d'inflation mensuelle équivalente. Nous avons fait figurer
entre parenthèses sur l'axe des ordonnées, à
côté de ch9ue niveau 7r d'inflation mensuelle, le taux
d'inflation annuel équivalent, défini par (1 +
7r)1 - 1. Il s'agit du taux d'inflation annuel
réalisé si 7rt =7r tout au long de
l'année.
7On peut en fait montrer que dans ces conditions, le
processus 1rt converge en loi quand t ? +oo vers un
processus stationnaire de loi normale N ~
b, a2
2a
23
Il convient de remarquer que des trajectoires avec des
périodes déflationnistes, bien que n'arrivant que très
rarement, sont également permises par ce modèle (pour la simple
raison que P(rt<0) > 0 pour tout t).
Ce modèle sur l'inflation sera utilisé pour
simuler des trajectoires d'évolution de l'encours. Nous reviendrons plus
en détail sur ce point dans la section dédiée.
| 


