4.2.4 Simulation de la solution exacte du modèle de
Vasicek
Aprés application du Lemme d'Itô, la solution du
modèle de Vasicek est :
r
1
rti+1 = e_k(ti+1_ti)rtj + 0(1 - e_k(ti+1_ti)) + ~ 2k(1
- e_2k(ti+1_ti))Zj+i (4.10)
(voir [4])
Nous simulerons le processus aux instants 0 = to < ti < :::
< tn
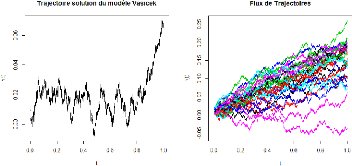
FIGURE 8.1 : Simulation de la solution FIGURE 8.2 : Un
echantillon de
exacte du modèle de Vasicek. 30 trajectoires.
4.2.5 Calcul du prix du bon dans le modèle de
Vasicek
Soit P(t, T) le prix d'une obligation zéro-coupon a
l'instant t dont l'échéance est a T
|
Le prix du bon est donné par:
|
|
P(t, T)
|
=
|
|
avec A(t, T )
|
=
|
|
et B(t,T)
|
=
|
R T
P (t, T ) = Et(e t --rudu) (4.11)
A(t, T)e_B(t;T)rt (4.12)
{ }
(0 - 2
2k2 )[B(t, T ) -- T + t] - 2
exp 4kB(t, T )2 (4.13)
k(1 - e_k(t_T))
1 (4.14)
(voir [6])
| 


