IV.2.2.2. Le problème de l'identification de
Ce problème consiste à déterminer si,
à partir des paramètres estimés de la forme
réduite, nous avons assez d'équations que d'inconnues pour
trouver les paramètres de la forme structurelle. Remarquons que :
la forme réduite comporte  paramètres49(*). En effet, nous avons  matrices carrées d'ordre  de coefficients des endogènes retardés ( ) soit  paramètres ;  composantes de la covariable exogène sur les  équations, c'est-à-dire  paramètres ; et la matrice de variance-covariance des
innovations qui est symétrique soit en plus  paramètres.
S'agissant de la forme structurelle, nous avons en plus des
paramètres de la forme réduite, ceux de la matrice des variables
contemporaines ( ) soit  paramètres supplémentaires. Or tous les
éléments de la diagonale de  étant égaux à l`unité,  n'a en tout que  paramètres inconnus. Comme  est diagonale, elle n'a que  paramètres inconnus. En définitive, la forme structurelle
a avec des paramètres inconnus de covariables exogènes un nombre
de paramètres égal à  .
Ainsi, la forme structurelle a  paramètres de plus que la forme réduite ; l'on dit
alors que le système est sous identifié. Pour pouvoir le
résoudre, il faudra qu'il soit au moins juste
identifié50(*), ce qui correspond donc à imposer  restrictions identifiantes sur les paramètres de la forme
structurelle. Dans le cas de la présente étude, puisque  , il faut imposer  restrictions.
3ème étape :
Démarche pour imposer les restrictions identifiantes.
Les contraintes identifiantes portent presque toujours sur les
réponses du système aux différentes impulsions
structurelles : le nombre  de contraintes identifiantes que le modélisateur doit introduire
en faisant référence à la théorie économique
croit rapidement avec la dimension du système et corrélativement,
le degré d'arbitraire inévitablement associé à
l'expression des a priori correspondants. En pratique, la théorie
économique ne fournit qu'un nombre très réduit de
contraintes identifiantes qui ne soit pas sujet à controverse. (Bruneau
et De Bandt (1998))
Plusieurs approches ont été proposées
dans la littérature pour imposer ces restrictions. Il existe une
façon simple, en effet, plus statistique que véritablement
économique, d'imposer les contraintes identifiantes
supplémentaires. C'est la décomposition de Choleski de la matrice
de variance  , définie comme l'unique matrice triangulaire inférieure
 telle que
 .
L'orthogonalisation des impulsions est alors
réalisée selon les principes préconisés par Sims
(1980), et ne requiert comme a priori que le choix de l'ordre des séries
qui doivent être alors rangées de la variable la plus
« exogène » à la plus
« endogène » : la matrice  correspondant à la décomposition de Choleski est
définie de manière unique pour un ordre donné des
composantes du modèle.
Il faut noter ici que l'orthogonalisation obtenue par la
méthode de Choleski a tout de même été
critiquée à de nombreuses reprises et les partisans de la
méthodologie VAR structurel préconisent l'orthogonalisation
fondée sur l'imposition de contraintes identifiantes tirées de la
théorie économique (voir par exemple Shapiro et Watson
(1989) ; Blanchard et Quah (1989), King et al. (1992) etc.).
A l'instar de Mialou (2002), qui a adopté la
démarche proposée par Blanchard et Quah (1989), nous utiliserons
plutôt la démarche dite
« formelle »51(*) qui se présente comme suit :
Si on note  l'unique matrice triangulaire obtenue par factorisation de Choleski de
 , toute matrice  telle que  est une transformation orthonormée de  . Aussi, la restriction que le coté supérieur droit de la
matrice  est égal à zéro est donc une restriction
orthogonale qui détermine de façon unique la transformation
orthonormée.52(*)
En considérant l'équation , l'on peut écrire la matrice d'impact de long terme comme
suit :
 
 est donc triangulaire inférieur et est un facteur de la matrice
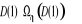 . Les restrictions peuvent donc être obtenues en imposant  comme étant le facteur de Choleski de cette matrice.
En posant  on a : 
et donc :
 
Cette matrice de passage peut être obtenue sans passer
par des algorithmes plus complexes permettant l'estimation des équations
non linéaires.
* 49 Il suffit de les
compter en utilisant les ordres des différentes matrices.
* 50 C'est-à-dire que
le nombre de paramètres inconnus soit au moins égal au nombre
d'équations.
* 51 Cette démarche
est en fait une variante de la décomposition de Choleski.
* 52 Cf. Blanchard et Quah
(1989).
| 
