Conception et modélisation d'un capteur acoustique

4.3.2 Céramique piézoélectrique de forme cylindrique

Considérons la céramique piézoélectrique de la figure 4.2.

X3 z

I3

a3

X2

V3

a

r

P + -

X1

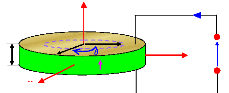
Fig. 4.2 -- Dimensions et système de coordonnées d'un disque céramique

Les hypothèses précédentes sont les mêmes. Seules changent les écritures des déplacements afin de tenir compte de la géométrie particulière de la céramique piézoélectrique. Dans le cas de vibrations radiales, on a [104]:

où (r, e, z) sont les cordonnées cylindriques.

La loi de newton est donnée par la relation [101] :

??T??j = ?? ??xj

a2ui at2 (4.18)

En introduisant les équations (4.17) dans l'équation (4.18), on obtient :

u_r = U_r?? 1(????)exp (j cut)

u_z = U_z sin(a3a3) exp (j cut) (4.19)

ue = 0

En reportant les expressions des déplacements selon r et z dans les relations (4.4) et (4.5), l'expression de l'impédance électrique « Z » de la céramique piézoélectrique sera :

Z=	1 j??0cu[^1	?? h31	h31 C^133 h33 C1^D3 R 2 ac/C33 43 aa0(aa)	h33		fl33 ?? ah33 h31C13D???? 0(????) El (4.20) ????C33^D 43 2????0(????)

avec

R = (70(aa)

tan

a3 a3

2 J

E=

a3 a3

(4.21)

2

c0 = Eg3n- a3

_a2

3a = aC ⁱf1a0 (aa) CD _a CD

12

- (aa)

et a0(aa) et a1(aa) sont respectivement les fonctions de Bessel de première espèce d'ordres 0 et1 de la variable « aa ».

L'expression de l'impédance électrique (relation 4.20) comporte deux termes : l'un est relatif aux modes radiaux (R) et l'autre au mode en épaisseur (E).

Les fréquences d'antirésonance pour le mode en épaisseur ont la meme expression que pour la céramique piézoélectrique en forme de plaque (cf. équation (4.16)).

4.3.3 Discussion

Du fait des hypothèses générales utilisées, les résultats de la modélisation tridimensionnelle (cf. tableau 4.1) sont valables quelques soient les dimensions de l'échantillon céramique :

· Pour la géométrie parallélépipédique, les résultats sont applicables aux cas d'une plaque ou barreau.

· Pour la géométrie cylindrique, les résultats sont applicables aux cas d'un disque ou cylindre.

De plus, ces résultats mettent clairement en évidence l'influence des couplages piézoélectrique ( _h31 ) et élastique ( c12 ?? , c13 ?? ) sur le comportement de la céramique piézoélectrique et montrent que les vitesses acoustiques et permittivités ne dépendent pas de la géométrie de l'échantillon.

Contrairement aux modèles unidimensionnels qui étaient applicables seulement autour d'une fréquence de résonance particulière, les modèles tridimensionnels sont valables à toutes les fréquences.

Remarquons que les expressions (4.13) et (4.20) se simplifient lorsque l'on considère que certains coefficients élastiques et piézoélectriques sont nuls. On retrouve alors les expressions unidimensionnelles correspondantes. Ce qui montre, a contrario, que pour établir les relations simplifiées, il faut supposer nuls les coefficients correspondants.

· Si on suppose c12 ??= c13 ??= 0 et h31 = 0, les expressions (4.13) et (4.20) se réduisent et on retrouve les expressions (3.4) et (D.2).

· Si on suppose c33 ?? = 0 et h33 = 0, l'expression (4.20) se réduit et on retrouve l'expression (D.1).