4.3 Expression tridimensionnelle de l'impédance
électri-
que d'une céramique
piézoélectrique
4.3.1 Céramique piézoélectrique de
forme parallélépipédique
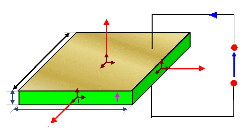
Considérons la céramique
piézoélectrique de la figure 4.1.
x3
a1
T4
T5
T6
T3
T4
T2
x2
V3
a3
T5 T6T
P +
-
1
a2
I3
x1
Fig. 4.1 - Dimensions et système de coordonnées
d'une plaque céramique
D'après [101], l'expression (4.1) peut s'écrire
:
u1 = U1sin(ax1) exp (jcut)
u2 = U2sin(ax2) exp (jcut) (4.6)
u3 = U3sin(a3x3) exp (jcut)
avec a = cu/vp est le nombre d'onde dans la céramique
selon une direction quelconque dans le plan « x1-x2 ».
Les différentes conditions aux limites
mécaniques sur les faces permettent de calculer les valeurs des
amplitudes : U1, U2 et U3 des ondes en fonction des coefficients
élastiques et piézoélectriques.
Sous la forme développée la relation (4.2)
s'écrit:
· T1 = 0 , pour x1 = #177;a1/2 et x2 et x3 arbitraires,
mais x2 E [--a2/2, a2/2 et x3 E [--a3/2, a3/2 ].
· T2 = 0 , pour x2 = #177;a2/2 et x1 et x3 arbitraires,
mais x1 E [--a1/2, a1/2 et x3 E [--a3/2, a3/2].
· T3 = 0 , pour x3 = #177;a3/2 et x1 et x2 arbitraires,
mais x1 E [--a1/2, a1/2 et x2 E [--a2/2, a2/2].
En reportant les relations (4.6) dans les expressions (4.4),
les polarisations des diverses ondes sont :
??1 =
??2 =
??3 =
avec
??1 =
??3 =
??1??0
??cos ????1/2)
(4.7)
(4.8)
??1??0
??cos ????2/2)
??3??0
??3cos ??3??3/2)
??
~31??33 ?? - ~33??13
?? 2
??11 ?? + ??12 ?? ~??33 ?? - 2??13
??
~33 ??11 ?? + ??12 ?? ~ - 231??13
?? 2
??11 ?? + ??12 ?? ~??33 ?? - 2??13
En reportant les relations (4.6) dans la relation (4.5) et en
prenant la ligne de champ correspondant à ??1 = ??2 = 0, on obtient :
1
+
????1
2 ~
?? ??3 ~??3 - ~33 + ??33 ?? ??3 (4.9)
????2 ????3
2 ~
cos
??3 = -~31??1
cos
1
En intégrant le champ électrique on obtiendra le
potentiel « ??3 » appliqué d'où :
[??3 = ??33?? - h31??1
|
1 1 ~ ??3 - 233??3 tan ??3??3
+
cos ????1 cos ????2 2 ~
??3
2 ~ 2 ~
|
??3 (4.10)
|
|
La charge totale sur les électrodes s'écrit
[101]:
?? = ??1??2??3 (4.11)
Le courant électrique est lié à la charge
totale sur les électrodes par la relation :
?? ??
??3 = = ????1??2????3 (4.12)
????
Par suite, l'expression de l'impédance
électrique «??» de la céramique
piézoélectrique sera :
1 - 2 ~31??13 ??
?? (4.13)
~31 ~33(??11 ?? + ??12 ?? )
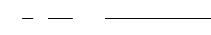
??3 ?? =
1 1 - ~31??33 ?? - ~33??13
=
??3 ????0?? ?? 2
??11 ?? + ??12 ?? ~??33 ?? - 2??13
??
?? ~ ?? + ???? 2

??33 ??13 ?? 2
1 - 2 ??
??11 ?? + ??12 ?? ~??33
avec
1 1
L=
cos
cos
aa2)
2
aa1) + 2
tan
E=
a3
a3a3\
2 )
??3a3
2
S a1 a2
C0 = 633
(4.14)
L'expression de l'impédance électrique
(relation 4.13) montre que le couplage des modes se manifeste par la
présence de deux termes : l'un est relatif aux modes latéraux
(L) et l'autre au mode en épaisseur
(E).
Les fréquences d'antirésonance des modes
latéraux et en épaisseur sont respectivement données par
les relations :
VP
fLi = (2n + 1) 2a ; i = 1 ou 2, n E N (4.15)
i
fE = (2n + 1)
|
VP3
; n E N (4.16)
2a3
|
|
| 


