Conception et modélisation d'un capteur acoustique

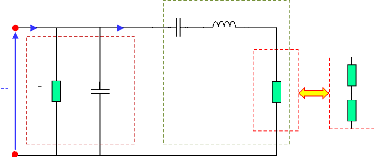
3.2.2.3 Schéma électrique équivalent simplifié du transducteur

3.2.2.3.1 Schéma électrique équivalent simplifié

D'une manière générale, au voisinage d'une de ses fréquences de résonance, le comportement du transducteur de faible charge acoustique est décrit par le schéma équivalent simplifié illustré sur la figure 3.10 [92].

V3

I3

I_m

C_m L_m

Branche statique

Branchgclynamique
ou motionnelle

R0

C0

R_m

R_a

Rb

Fig. 3.10 - Schéma électrique équivalent simplifié du transducteur [93]

où

· R0 est une résistance représentant les pertes diélectriques. Elles se relié à la tangente l'angle de pertes diélectrique par [39]:

1

R0 = (3.18)

C0o.tanS_e

· R_a est une résistance dans laquelle se dissipe une énergie égale à l'énergie mécanique rayonnée par la céramique.

· Rb est une résistance qui traduit les pertes mécaniques dans le matériau.

· La résistance : R_m= R_a+Rb.

· L'inductance « L_m » est proportionnelle à la masse de la céramique.

· La capacité « C_m » est proportionnelle à l'élasticité de la céramique.

· I_m est le courant motionnel.

La branche statique du schéma équivalent traduisant les propriétés purement diélectriques, formée par la mise en parallèle de R0 et C0. La valeur très élevée de R0 permet dans la plupart des cas de négliger cette branche.

La branche motionnelle du schéma équivalent traduisant les propriétés mécaniques de l'élément vibrant constituée par la mise en série de R_m, C_m et Lm.

Les fréquences de résonance « ????, ????» associées respectivement au circuit oscillant série (formé par la branche motionnelle) et au circuit oscillant parallèle (formé par l'association de la branche électrique et motionnelle) sont donnés par les relations [39]:

		1
???? =			(3.19)
	2?? ????	????
		1
???? =			(3.20)
	2?? ????	??0????
					Le coefficient de couplage électromécanique est donné par [18]:
???? =	~????		(3.21)

3.2.2.3.2 Identification des paramètres du schéma électrique équivalent simplifié 3.2.2.3.2.1 Procédé d'identification

L'identification des paramètres du schéma équivalent simplifié se fait à partir du tracé de l'admittance électrique du transducteur « Y » dans le diagramme de Bode (cf. figure 3.11.a) et dans le plan de Nyquist (cf. figure 3.11.b).

Le tracé de l'admittance dans le plan de Bode fait apparaitre les phénomènes de résonance (admittance maximale pour « ???? ») et d'antirésonance (admittance minimale pour « ???? ») qui sont respectivement proches des fréquences ???? et ????.

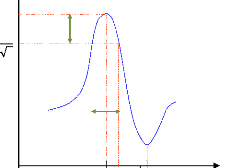
Les éléments du circuit équivalent sont déterminés à partir du tracé de l'admittance dans le plan de Nyquist avec les relations [47,94]:

· Résistance ??0 :

· · · ·	Résistance ???? : Capacité ??0 : Capacité ???? : Inductance ???? :	??0 ???? ??0 ???? ????	1	?? ; ????????	« ???? (3.22) (3.23) 3.24) (3.25) (3.26)
			= R?? (??(??)) 1 =
			R?? ?? ????~ - I?? ?? ????)
				1 ??0
			= ???? 2 ??0 ????^2 - ???? 2 ~
			= ???? 1 =
			??0 (????^2 - fs2)

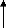
YM

Y_m

Ym

2

3dB

Af

Résonance

Antirésonance

f

f M		f m
fs		f p

(a)

C0

L_m C_m

??0

f 2

??0 + Rm

f 1

f

f M

fs

f p Conductance R_e (Y)

1

f

1

f m

f a f r

(b)

Susceptance 3_m(Y)

3.2.2.3.2.2 Simulation de l'admittance électrique

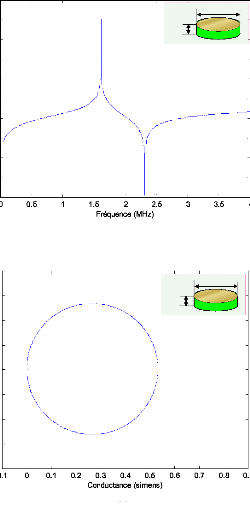
La figure 3.12 montre le tracé de l'admittance électrique d'un disque céramique de type PZT503 dans le plan de Nyquist.

1mm

16mm

PZT503

(a)

(c)

1mm

16mm

PZT503

Fig. 3.12 - Tracé simulé de l'admittance électrique: (a) Dans le diagramme de Bode, (b)
Dans le plan de Nyquist

^{3 35} 4

3.2.2.3.2.3 Identification des paramètres

A partir des résultats de simulation précédents, les différents paramètres du schéma électrique équivalent simplifié sont déduits et résumés dans le tableau 3.3.

Paramètres	valeur	Unité
fr	1.61	MHz
fa	2.31
R0	1.98	kÙ
C0	989	pF
Rm	1.21	Ù
Lm	9330	mH
Cm	1050	pF

Tab. 3.3 - Paramètres du schéma électrique équivalent simplifié