3.2.2 Transducteur avec pertes
La modélisation d'une façon précise d'un
système de transduction électromécanique exige l'ensemble
des propriétés électromécaniques pour chacun des
éléments constitutifs du système. La réponse
dynamique d'un tel système ne sera caractérisée avec
précision que si les propriétés
électromécaniques avec pertes pour chacun des
éléments constitutifs de ce système ont introduit dans le
modèle [89]. Le transducteur ultrasonore piézoélectrique
est soumis à un ensemble de pertes d'une grande importance lors de la
modélisation. Il s'agit notamment de pertes mécaniques et
diélectriques dans le matériau actif (i.e. céramique
piézoélectrique), pertes mécaniques dans les
matériaux passifs tels que le matériau absorbant et lame
d'adaptation d'impédance.
3.2.2.1 Différents types de pertes
3.2.2.1.1 Pertes diélectriques
Lors de leur fonctionnement, les céramiques
piézoélectriques dissipent une puissance non négligeable,
correspondant aux pertes d'origine diélectrique. Ces pertes se
traduisent sous forme de chaleur, ce qui, à terme, provoque la perte des
propriétés piézoélectrique [42]. Elles sont souvent
représentées au travers de la tangente de l'angle de pertes
diélectriques « ?????????? ». Dans ce cas, on définit
une permittivité complexe, dont la partie
imaginaire est fonction de ?????????? [90] :
??33??' = ??33?? 1 - ????????????)
(3.15)
où ??33??' et ??33?? sont
respectivement les permittivites de la ceramique avec et sont pertes.
3.2.2.1.2 Pertes mécaniques
Les pertes mecaniques, qui sont une consequence de la
propagation de l'onde acoustique dans les materiaux actifs ou passifs et sont
dues aux frottements internes generes dans ces materiaux. Elles sont
quantifiées par la tangente de l'angle de pertes mécaniques
??????????. Dans ce cas, on definie une constante elastique complexe dont la
partie imaginaire est fonction de ?????????? [91] :
??33??' = ??33?? 1 + ????????????)
(3.16)
où ??33??' et ??33?? sont
respectivement les constants elastiques de la ceramique avec et sont pertes.
3.2.2.2 Impédance électrique avec pertes
du transducteur
3.2.2.2.1 Expression de l'impédance
électrique avec pertes
Pour modeliser les pertes dans le transducteur (resonateur
libre), nous introduisons les parties imaginaires des paramètres
complexes (equations (3.15) et (3.16)) dans la relation (3.4), ceci nous permet
d'expliciter l'impédance electrique avec pertes10 :
1
??=
1 - ????2 1 - ????????????
??????0(1 - ????????????)
1 + ?? ??????????
2
?????? (?????? ?? 1 - ?? ?????????? ))
(3.17)
2 2
??
2
3.2.2.2.2 Simulation de l'impédance
électrique avec pertes
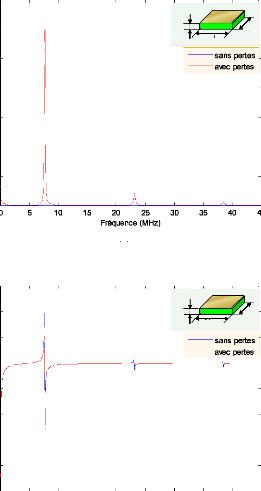
La figure 3.9 montre pour une ceramique piezoelectrique de
type PZT503, l'évolution de la résistance et réactance de
l'impédance electrique d'une plaque de dimensions 20 × 20 ×
0.3 ????. Nous constatons que les pertes dielectrique et mecanique entrainent
la variation de la resistance. Il nous faut donc completer le modèle du
transducteur sans pertes en y ajoutant des elements electriques resistifs.
10 Le developpement limite de Taylor d'ordre "1" est utilise
afin d'effectuer des approximations sur les differents paramètres de
notre modèle et par consequent un modèle simple est obtenu.
0.3
mm
20
PZT503
mm
mm
20
(a)
0.3
mm
20
PZT503
mm
mm
20
(b)pert
Fig. 3.9 - Courbe simulée de
l'impédance;(a) Résistance, (b) Réactance
| 


