3.3 Simulation d'un transducteur ultrasonore
piézoélec-
trique
Dans cette partie, parmi les schémas équivalents
que nous avons décrits (cf. § 3.2.1.3), le modèle de Leach
à été choisi pour réaliser nos simulations, car il
utilise des sources contrôlées au lieu du transformateur.
L'utilisation des sources contrôlées entraîne la disparition
de la capacité négative comme dans le modèle de Mason et
du transformateur dont le rapport de transformation varie en fonction de la
fréquence comme dans le modèle KLM.
3.3.1 Caractérisation de la ligne de transmission et
analogie électroacoustique
Une onde ultrasonore se propageant dans un milieu peut
être décrite comme une perturbation à laquelle le milieu
réagit. De même, dans une ligne de transmission électrique
une impulsion électrique peut se propager à travers elle. Cette
impulsion est reçue à l'autre extrémité de la ligne
après un temps très court, mais fini et une certaine vitesse. Par
analogie à l'onde ultrasonore, l'impulsion électrique est la
concentration et raréfaction des électrons à
l'intérieur d'une ligne de transmission électrique [98].
Une ligne de transmission acoustique est
caractérisée de façon similaire à une ligne de
transmission électrique. Une analogie électro-acoustique (cf.
annexe C) établit une correspondance entre une ligne de transmission
électrique et une transmission d'onde acoustique. Cette correspondance
permet ainsi de modéliser simplement le comportement d'une ligne de
transmission [5].
La ligne de transmission avec pertes est
modélisée par un quadripôle, avec une tension et un courant
d'entrée et de sortie [79]. Ce quadripôle est lui-même
constitué de plusieurs dipôles passifs appelés
paramètres primaires de ligne comme le montre la figure 3.13.
I(x,t) R.dx L.dx I(x+dx,t)
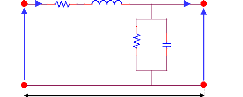
V(x,t) G.dx C.dx V(x+dx,t)
dx
Fig. 3.13 - Schéma électrique équivalent
d'une ligne de transmission de longueur ????
avec
· R est la résistance linéique.
· L est l'inductance linéique.
· C est la capacité linéique.
· G est la conductance linéique.
· ??(??, ??)et ?? ??, ??) sont respectivement le courant et
tension d'entré de la ligne.
· ??(?? + ????, ??)et ?? ?? + ????, ??) sont respectivement
le courant et tension de sortie de la
ligne.
Les paramètres secondaires (Ze,ã),
sont exprimés en fonction des paramètres primaires de la ligne
(R,L,C,G). Ainsi, l'impédance caractéristique
électrique et la constante de propagation sont respectivement
données par [99]:
7 R+jùL
(3.27)
Ze iG+jùC
et
ã = R+jùL~(G+jùC) =??????
+j?????? (3.28)
Pour un milieu acoustique avec pertes, l'impédance
caractéristique acoustique est exprimée par la relation [96]:
Za=ñva 1+jùô
(3.29)
avec ô est le temps de relaxation.
En faisant un développement limité sur les
équations (3.27) et (3.28), on obtient :
Ze?JL C 1+ 1
2jù R L - G C (3.30)
et
1
ã? 2 LC

+jù LC (3.31)
R G
L + C

1
2 LC
1
+ 2 LC
G
C (3.36)
?????? =
R
L

Dans le cas de pertes faibles, mais non négligeables
où R«ùL et G«ùC et
ùô«1, les impédances caractéristiques :
électrique (équation 3.30) et acoustique (équation 3.29)
sont
respectivement approximée par : Ze? L
?? et Za? ñva. Pour corréler
les deux impédances caractéristiques, on utilise l'analogie entre
les grandeurs électriques et acoustiques (cf. annexe C).
L'équivalence entre les deux systèmes est donnée par
[98]:
Ze= ZaA (3.32)
avec A est la section de la céramique
piézoélectrique perpendiculaire au sens de la propagation des
ondes acoustiques.
La vitesse de propagation dans le milieu acoustique
s'écrit [95]:
1
va = LC (3.33)
En utilisant les équations (3.32) et (3.33), on obtient
les relations suivantes:
L? Añ (3.34)
1
C= Añva (3.35)
La partie réelle de l'équation (3.31) est la
constante d'atténuation :
Dans la théorie classique de l'atténuation
acoustique, la constante d'atténuation s'écrit [79]:
aaclassique =????v +????t (3.37)
avec aav est le coefficient d'atténuation
dû aux pertes visqueuses, et aat est le coefficient
d'atténuation dû à la conduction thermique.
En utilisant les équations (3.34), (3.35), (3.36) et
(3.37), les relations suivantes peuvent être obtenues :
R= 2ñvaA????v (3.38)
2
G= ñAva aat (3.39)
| 


