Conception et modélisation d'un capteur acoustique

3.2.1.2 Impédance électrique du transducteur

3.2.1.2.1 Expression de l'impédance électrique

En utilisant les équations de la piézoélectricité (cf. § 1.5), on peut mettre en relation les grandeurs électriques et mécaniques (cf. figure 3.1) sous forme matricielle [82,83]:

??1 ~ ??2 ~ = -?? ??3

????0?????? ??3??3 ????0??????????(??3??3) h33

????0?????????? ??3??3 ????0?????? ??3??3 h33

h33 ?? h33 ?? 1

??11 ??2 (3.1) ??3

?? ?? ????0

Dans le cas d'un transducteur (matériau piézoélectrique métallisé d'impédance Z_p) ,dont on néglige l'épaisseur des électrodes et chargé par deux milieux d'impédances Z1 et Z2 respixtivement en face arrière et en face avant du transducteur, l'impédance électrique d'entrée se calcule á partir de la matrice des impédances (cf. équation (3.1)) [84] :

où

??=

??3 ??3

1

????0 ??

1 +

??

(3.2)

Id 2?? ?? 1 - cosö) ? j Z1 + Z2)sinö

???? 2

- ???? + ??1??2)???????? + ^??????(??1 + ??2)????????)

· ??0 est l'impédance acoustique spécifique du matériau piézoélectrique.

· ??3 est le nombre d'onde associé à la pulsation «ù» et á la vitesse des ondes ultrasonores dans la céramique«????3» selon l'axe de polarisation «x3» (??3 = ??/????3).

· L'angle ö est défini comme ?? = ??3??3.

· h33est la constante piézoélectrique.

· ???? est le coefficient de couplage électromécanique en épaisseur.

· ??0 est la capacité statique du transducteur rigidement lié (clampé) définie par [6] :

??33 ?? ??

??0 = (3.3)

??3

Remarque :

La relation (3.2) souligne l'importance de la constante de couplage comme le principal paramètre piézo-électrique caractérisant le transducteur. Il est aussi clair que le rapport 1/????0 module l'impédance électrique du transducteur en fonction de la fréquence.

3.2.1.2.2 Caractérisation du transducteur

Pour caractériser le transducteur, on peut utiliser une configuration mécanique du type résonateur libre [80]. Dans ce cas, le transducteur est sans charge avant et arrière (i.e. Z1=Z2=0 ). L'impédance électrique s'écrit d'après l'équation (3.2):

1 1 - ????2 tan ??/2~

(3.4)

?? = ??/2 ~

??????0

L'impédance tend vers l'infini (i.e. admittance ?? = 1/?? s'annule) pour chaque multiple de ???? , la fréquence d'antirésonance :

????(??) = 2?? + 1)??_?? ; avec ???? = ????3 (2??3) et ?? ? N (3.5)

L'impédance s'annule (i.e. admittance tend vers l'infini) pour les fréquences de résonances ????(??) avec ?? ? N, ce qui d'après l'équation (3.4) nous donne :

(??) (??)

????2?????? ~?? ???? ~ = ?? ???? 2 f_a 2 fa (3.6)

Le mode fondamentale est donné par ?? = 0 et les harmoniques sont de fréquences multiples impaires de la fréquence fondamentale.

Pour caractériser un transducteur, on mesure les fréquences de résonance et d'antirésonance, ce qui donne la vitesse acoustique et le coefficient de couplage électromécanique ???? :

????3 = ²??????3 (3.7)

???? = ~?? ???? ?????? ?? ????-???? (3.8)

2 ???? 2 ????

Il est important de noter que l'épaisseur de la céramique piézoélectrique fixe la fréquence d'antirésonance et non la fréquence de résonance. La fréquence de résonance est elle-même liée au coefficient de couplage électromécanique du matériau piézoélectrique.

En pratique, c'est la mesure des fréquences de résonance et d'antirésonance qui fournit la valeur du coefficient de couplage électromécanique [24]:

· Coefficient de couplage en fonction du rapport Ir/Ia

La figure 3.2 montre la variation du coefficient de couplage électromécanique en fonction du rapport «f??/f?? » (cf. équation (3.8)). On peut observer que plus le rapport «f??/f?? » est faible (i.e. l'intervalle de fréquence entre la résonance et l'antirésonance est élevé) plus le coefficient de couplage est grand.

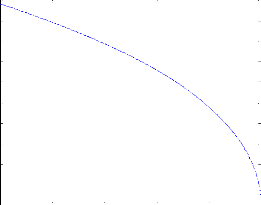
Fig. 3.2- Variation du coefficient de couplage en fonction de «f??/f?? »

· Influence de l'épaisseur de la céramique sur la fréquence d'antirésonance

La figure 3.3 montre pour une céramique piézoélectrique de type PZT503, l'évolution de la fréquence d'antirésonance définie par l'équation 3.7. On comprend facilement qu'une montée en fréquence nécessite une diminution de l'épaisseur. L'utilisation des céramiques massives permet de couvrir une gamme de fréquence qui s'étend du « kHz » à la centaine de « MHz ». Pour des fréquences de l'ordre du « GHz », l'épaisseur de la céramique s'amenuise à quelques microns. Donc alors, il est nécessaire d'avoir recours à des couches (ou films) piézoélectriques déposées par des techniques relevant du domaine de la microélectronique, tout en gardant des propriétés électromécaniques équivalentes à celles obtenues par les procédés classiques.

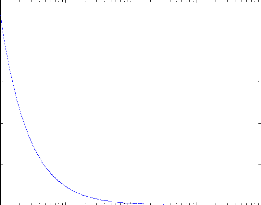
a3 (m)

Fig. 3.3 - Variation de la fréquence d'antirésonance en fonction de l'épaisseur Remarque :

Pour obtenir une puissance acoustique convenable, il faut travailler dans des conditions de résonance. Pour cela, il faut choisir la fréquence f0 de la source d'excitation de telle sorte que l'épaisseur de la céramique piézoélectrique soit [33]:

a3 = (2n + 1)

A0 2

= (2n + 1) Vp3 (3.10) 2f0

Le fondamental A0/2 est le plus recherché, car il correspond aux pertes les plus faibles dans le matériau piézoélectrique, puisque le parcours des ondes acoustiques y est le plus réduit.

3.2.1.2.3 Simulation de l'impédance électrique

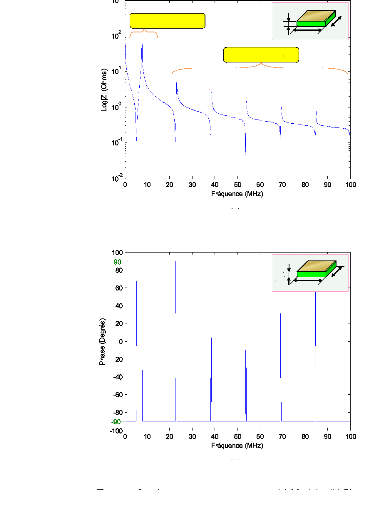
La figure 3.4 montre, pour une plaque céramique de type PZT503, la variation du module et phase de l'impédance en fréquence. On constate que pour le mode de résonance fondamental ils associent des modes parasites (ou partiels).

· Pour le mode fondamental, les fréquences de résonances et d'antirésonances sont respectivement : 5.5MHz, 7.7 MHz.

· Pour les modes parasites :

- Les fréquences de résonances sont : 22.5 MHz, 38 MHz, 53.9 MHz, 69.1 MHz, 5 84.5 MHz.

- Les fréquences d'antirésonance sont : 23.1 MHz, 38.5 MHz, 53.9 MHz, 69.3 MHz, 84.7 MHz.

(a)

PZT503

20

mm

20

(b)

Fig. 3.4 - Courbe simulée de l'impédance ; (a) Module; (b) Phase

0.3

mm

mm

PZT503

Mode fondamental

20

0.3

mm

mm

20

mm

????

Modes parasites

???? (1)

???? (2)

???? (3)

???? (1) ???? (2)

????

???? (3) ???? (4) ???? (5)

(5)

???? (4) ????

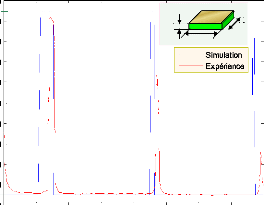
3.2.1.2.4 Validation des résultats de simulation

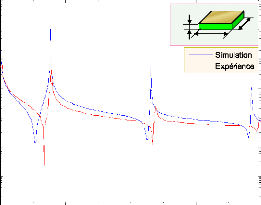
Pour permettre la validation des résultats de simulation précédents, les résultats expérimentaux (courbe de l'impédance et celle de la phase) donnés dans la référence [85] sont utilisés. La figure 3.5 illustre les variations du module et phase de l'impédance en fonction de la fréquence. Nous remarquons que la concordance entre les positions des fréquences de résonance et d'antirésonance est bonne.

0.3

mm

20

PZT503

mm

mm

20

(a)

(b)

0.3

mm

20

PZT503

mm

mm

20

Les valeurs des fréquences de résonances et d'antirésonances expérimentales sont comparées celles issues de l'approche analytique et résumées dans le tableau 3.1. Nous constatons que les fréquences expérimentales sont cohérentes avec celles théoriques :

Fréquences (MHz)	Théorie	Expérimentale	Erreur relative (%)
????	5.5	6.9	20
???? (1)	22.5	23.5	4
???? (2)	38	39.3	3
????	7.7	7.9	2.5
???? (1)	23.1	23.8	3
???? (2)	38.5	39.7	3

Tab. 3.1 - Comparaison des valeurs des fréquences théoriques et expérimentales

A partir des résultats précédents, le facteur de couplage électromécanique et vitesse acoustique (cf. équations : 3.7, 3.8 et 3.9) sont déduits et récapitulés dans le tableau 3.2.

Paramètres	Théorie	Expérimentale
????	0.73	0.49
????3	4620	4740

Tab. 3.2 - Facteurs de couplage et vitesse acoustique théoriques et expérimentaux