Pour bien répondre à ses objectifs, notre travail
aura cinq chapitres, hormis l'introduction et la conclusion :
· Dans le premier, nous établirons le modèle
cinématique du robot dans sa plus simple expression ;
· Dans le second, nous établirons son modèle
dynamique dans sa forme la plus simple ;
· Ensuite les diverses améliorations (voir plus
loin) seront introduites ;
· Dans le quatrième chapitre, nous décrirons
l'architecture du programme de simulation ;
· Finalement, il s'agira de valider le code et
interpréter les résultats.
PRESENTATION DU PROBLEME
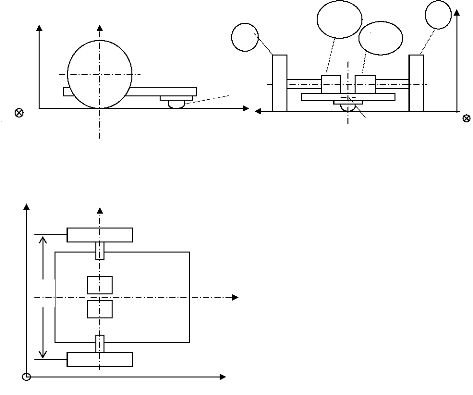
Le robot est constitué de deux roues motrices (1 et 3)
actionnées indépendamment par deux moteurs à courant
continu (M1 et M3) solidaires au châssis (2) du robot. Le
troisième point d'appui est constitué d'une bille libre (B) qui
n'est pas motorisée (Figure 1). Le robot se déplace sur un plan
incliné d'un angle â par rapport à
l'horizontale.
y1
y
O
z1
G1
x
M3
M1
G
G1
1
z
G3
B
3
z
y
O
y
l13
x1
x
Figure 1 : Projections orthogonales du
robot
Par ce projet, on devra arriver à prédire la
position, la vitesse et l'accélération du centre de masse du
robot (sorties) à partir des valeurs de couples fournis par les moteurs
ou à partir des courants appliqués à ceux-ci
(entrées).
Nous partirons d'un modèle simple sans frottement,
roulant sans glisser sur un sol plat. Ensuite, différentes
améliorations seront prises en compte. C'est notamment ;
· La prise en compte de l'inclinaison â ;
· La prise en compte du frottement dans les
différentes liaisons du robot (roues - châssis, roues-sol) ;
· La prise en compte de la dynamique des moteurs à
courant continu ;
· La prise en compte de la limite d'adhérence des
roues (roulement avec glissement sur le sol).
Nous considérerons que le robot est parfaitement
symétrique (les axes des roues coïncident aussi parfaitement) et
que les roues sont infiniment fines (existence d'un seul point de contact avec
le sol).
Pour établir les équations de mouvement, deux
méthodes équivalentes seront utilisées pour être
comparées. Il s'agit de la méthode analytique ou méthode
de LAGRANGE et celle des théorèmes
généraux ou méthode synthétique. Une d'elle sera
implémentée dans MATLAB pour la
résolution et il faudra choisir l'outil de résolution
numérique entre SIMULINK et les solveurs
ODE (Ordinary Differential Equation).
Les chiffres entre crochets renvoient à la
bibliographie.



