Modélisation et simulation d'un robot mobile sur roues avec le logiciel Matlab/Simulink

Chapitre 4 : DESCRIPTION DE L'ARCHITECTURE DU
PROGRAMME

Intervalle d'intégration

Equation différentielle d'ordre n

Changement des variables

Système d'équations
différentielles d'ordre 1
[Y']=f ([Y])

Intégration du système

Vecteur [Y]

Conditions initiales

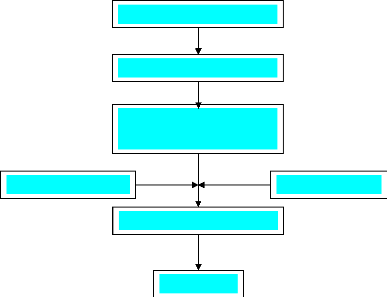
1. Généralités

1.1 But du chapitre

Ce chapitre a pour but de décrire et représenter l'enchaînement des opérations à

effectuer par ordre chronologique dans l'exécution du programme.

1.2 Résolution numérique d'une équation différentielle ordinaire d'ordre n Pour résoudre numériquement une équation différentielle ordinaire, on suit les

étapes suivantes :

· Changement de variables ;

· Transformation de l'équation en un système d'équations différentielles d'ordre un ;

· Intégration du système avec un solveur ode.

En résumé, on a :

1.3. Développement des intégrateurs numériques utilisés par le logiciel MATLAB

1. Forme canonique d'une EDO (équation différentielle ordinaire).

Equation : f ( y , t ) dy = dt

(126)

Condition initiale : y ( t _o ) = yo

Solution exacte : y = F (t)

Ou bien = + ?

t

f (y , t )dt

(127)

0

2. Transformation vers une forme canonique

d z

2

n - 1

dz d z

ⁿ d z

Soit l'équation : = G z

( , , ,..., ₁ , )

t

ⁿ dt ²

dt dt dt n -

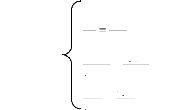
y 2

1 =

dt

dt

n

n

d

dy

z

=

dt

n

dt

z y

= 1

dz

dy

On posera :

n

-

dy

dt

1 =

y n

1

-

n

d

z

=

1

-

n

dt

(128)

f

( t , y)

Si :

dy

=

dt

y t _o= y_o

t

(129)

alors, la solution exacte sera : = + ?

y t y o f t y dt

( ) ( , )

0

Pour une solution numérique y_j , l'erreur commise sera : e j = y_j-y( t _j) (130)

3. Méthodes à pas constant

1) Méthode d'EULER ou de la tangente Soit à résoudre l'équation différentielle :

dy = dt

f ( y , t )

Considérons le développement de TAYLOR de y(t) autour de t_o, qui s'écrit :

) (131)

n

y t

' ' ( ) y t

( ) ( )

o n o

y t y t

( ) ( ) ( ) . ' ( ) ( ) .

2

= + -

t t y t + -

t t + + -

( ) .

t t + R t

n (

o o o o o

n

²! !

En se limitant à l'ordre 1 dans ce développement, on a :

y ( t ) = y(t _o ) + ( t - t _o ) .y ' ( t _o) (132)

Ou bien :

y n + = y _n + h f t _n y n (133)

. ( , )

1

Avec :

h = t n +1 -t n (134)

Les expressions (133) et (134) définissent la méthode d'EULER. Elle revient à estimer la solution au voisinage de t_n sur la tangente à la fonction f (t, y). Elle est assez précise pour des pas petits.

2) Méthode de HEUN

C'est une méthode en 4 étapes qui sont :

· Calcul de la fonction f en tj-1 :

k₁ = f( t j -1, y j -1) (135)

· Calcul de yj^* par la méthode de EULER explicite :
y j * = y j - + h.k (136)

1 1

· Calcul de la pente en (tj , yj *) :
k₂ = f(t _j , y _j ) (137)

· Calcul final de la solution finale entre k1 et k2 :

y j y j = - 1

k k + 1 2 + h . (138) 2

3) Méthodes de RUNGE-KUTTA (RK)-ODE 23 et ODE 45

Elles sont une amélioration de la méthode de HEUN et elles font la moyenne entre m

pentes.

Formule générique :

y j = y+ w₁. k ₁ + w₂ .k ₂ + + wm.k m (139)

Avec :

k1 = f ( t j -1, y j-1)

k 2 = f ( t + c2.h , y + a21.k1

)

)

k = f t j - + c h y j - + a k + a k

( . , . .

3 1 3 1 31 1 32 2

k f t

= ( + c h y

. , + a k a k

. + . ....

+ + a . )

k (140)

m j - 1 m j - 1 m 1 1 m 2 2 m m

( 1 )

- m - ¹

L'ordre m de la méthode dépend de l'ordre du développement de la série de TAYLOR correspondante.

Les termes wi, ci et ai sont choisi par identification avec les termes du développement de TAYLOR à l'ordre m. Pour faire cette identification, on arrive toujours à un système de n équations à n+1 inconnues. On doit alors fixer un paramètre au choix, lequel choix étant fait de manière à minimiser l'erreur d'intégration.

On voit bien que la méthode de HEUN est une méthode de RK d'ordre 2 avec c2=a21=1, w1= w2=1/2.

La méthode de RK d'ordre 4(RK4), s'écrit :

1 1 1 1

y j y j h k k k k

= - +

1 .( 1 + + + ) (141)

2 3 4

6 3 3 6

Avec :

k1 = f ( t j -1 , y j-1)

)
)

k 2 = f( t +^h ,y + h .

2 j2

k 3 = f( t +h 2 j2

, y + h k2

k_m = f( t j - ₁+ h,y j - ₁+ h.k₃ ) (142)

La précision de la méthode dépend de l'ordre, cependant l'utilisation d'ordres supérieurs n'est pas très intéressante. Cette précision augmente lorsque le pas h diminue. [3.3]

4. Méthode à pas variable

C'est une méthode numérique qui ajuste le pas d'intégration au cours de la résolution. Pour cela, il faut estimer l'erreur commise à chaque pas d'intégration. Si l'erreur d'intégration est trop grande, par rapport à un critère fixé, alors on réduit le pas h. Si l'erreur est petite, par rapport au même critère, on peut alors se permettre d'augmenter le pas pour aller plus vite. Deux solutions sont en vue :

· Solution 1 : Calculer une solution à un point donné avec deux valeurs de h différentes :

o Si le résultat est le même, alors on conserve la valeur grande de h pour le pas suivant ;

o Si le résultat est différent, on suppose que le meilleur résultat est obtenu avec la petite valeur de h qu'on conserve pour le pas suivant.

· Solution 2 : Utiliser deux méthodes en parallèle avec le même pas h mais avec des ordres différents.

Cette solution nous conduit aux solveurs ODE 45 et ODE 23 implantés dans MATLAB :

o ODE 23 : C'est la méthode de RK-FEHLBERG 23 qui utilise les méthodes de RK d'ordres 2 et 3 :

On calcule successivement yjavec RK2, yj^* avec RK3 et ?j = yj - yj^* (avec un même pas h) :

Si la valeur de ?j est inférieure à la tolérance fixée, alors on accepte yj tout en maintenant h ;

Si la valeur ?j est très petite que la tolérance fixée, alors on accepte yj et on augmente h ;

Si la valeur de ?j est supérieure à la tolérance fixée, alors on recommence avec h plus petit.

Comme c'est la méthode numérique qui choisit le pas, on n'a pas la
solution aux temps désirés. Il est alors nécessaire d'interpoler les résultats.

Cet intégrateur a un bas niveau d'exactitude et est utilisé pour des problèmes non raides avec tolérances brutes ou pour résoudre des problèmes modérément raides.[]

o ODE 45 : Ici les ordres sont 4 et 5. Cet intégrateur est employé la majeur partie du temps et il est le premier en vue pour tout problème. Il a un niveau moyen d'exactitude. [3.3], []

Pour ces deux méthodes, le pas d'intégration est fixé de manière à avoir :

ô -< max(Re lTol * y_j ,AbsTol) (143)

ti étant une estimation de l'erreur locale produite par la méthode numérique .

La tolérance relative (RelTol) et la tolérance absolue (AbsTol) sont respectivement 1^e-3 et 1e-6 par défaut.

5. Méthodes à pas liés

Elles consistent à évaluer yj à partir de plusieures valeurs yj-1, yj-2,....yj-k :

t_j

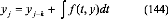
k

-

tj

Avec ces méthodes, f(t,y) sera évalué avec un polynôme d'interpolation. 1) Méthode ouverte

On utilise les k+1 dernières valeurs de f pour construire un polynôme de degrés k(f_n, fn- 1, fn-2,..., fn-k+1), lequel sera utilisé pour déduire la valeur de la fonction f en n+1 (une extrapolation). C'est la méthode d'ADAMS - BASHFORH (à pas fixe).

Pour k=1 :

y n + 1 = yn + h.f ( y n) (145)

Pour k=2 :

y j = yj-k + ? f( t , y ) dt (144)

3 1

2

y n + 1 = y _n h . ₂ .f( y _n ) - .f( yn-01_] (146)

Pour k=3 :

= + ? 23 16 5 ?

y y h f y

. . ( ) - . ( )

f y + . ( )

f y (147)

n + 1 n n n - 1 n - 2

?? 12 12 12 ??

Pour k=4 :

? 55 59 37 9 ?

y = +

y h f y

. . ( ) - . ( )

f y + . ( )

f y - . ( )

f y (148)

n + 1 n n n - 1 n - 2 n - 3

?? 24 24 24 24 ??

2) Méthode fermée

Contrairement à la méthode ouverte, on utilise cette fois le point qu'on cherche dans la détermination du polynôme d'interpolation de degré _k+1(fn+1, ^fn, fn-1, fn-2,..., fn-k+1). La méthode étant implicite, la résolution est donc lourde. C'est la méthode d'ADAMS - MOULTON (à pas fixe).

Pour k=0 :

y n + 1 = y_n + h. f ( y n +1) (149)

Pour k=1 :

1 1 ?

y y h f y

+ = + ? + +

. . ( ) . ( )

f y (150)

n 1 n n 1 n

?? 2 2 ??

Pour k=2 :

= + ? 5 8 1 ?

y y h f y

. . ( ) + . ( )

f y - . ( )

f y (151)

n + 1 n n + 1 n n - 1

?? 12 12 12 ??

Pour k=3 :

? 9 19 5 1 ?

y = +

y h f y

. . ( ) + . ( )

f y - . ( )

f y + . ( )

f y (152)

n + 1 n n + 1 n n - 1 n - 2

?? 24 24 24 24 ??

3) Méthode prédicteur - correcteur-ODE 113

Dans cette méthode, on utilise les avantages des méthodes ouvertes et fermées. Elle s'effectue en trois étapes :

· Etape 1 : Phase de prédiction :

^

On prédit une valeur 1

y n + de par la méthode ouverte ;

· Etape 2 : Phase d'évaluation :

^ ^

)

f n + = f t n + y n +

( , 1

1 1

· Etape 3 : Phase de correction :

^

On corrige la valeur de 1

y n +

^

.

en utilisant 1

f n +

Amélioration :

par une méthode fermée pour trouver yn+1

o La phase de correction peut être répétée plusieurs fois ;

o Usage d'une méthode à pas variable ;

o Usage d'une méthode à ordre du polynôme d'interpolation variable. Cette méthode a pour inconvénient majeur quelle n'est pas auto démarrante.

Si l'ordre est 1, la méthode est dite de EULER modifiée.

y n + prédit = y _n + h f t _n y n

1 , . ( , ) (153)

y corrigé y h f t y prédit

, = + . ( , , ) (154)

n + 1 n n + 1 n + 1

Le solveur ODE 113 de MATLAB utilise la méthode prédicteur - correcteur (méthode d'ADAMS - BASHFORTH - MOULTON à pas variable et ordre de polynôme variable entre 1 et 13). Il est utilisé pour des problèmes non raides avec des tolérances rigoureuses ou pour résoudre des problèmes intensifs avec une exactitude allant du niveau bas au haut niveau

A forte précision demandée, le solveur ODE 113 est plus rapide, tandis qu'à faible précision, les solveurs ODE 23 et 45 sont plus rapides.

6. Méthodes « stiff »

1) Equation différentielle « stiff »

Un système d'équations différentielles est « stiff » ou raide quand les dynamiques qu'il représente sont à la fois très lentes et très rapides.

¹ f y y y t

= 1 ( ₁ , ₂ ,..., , )

n

dt

dy

² f y y y t

= 2 ( ₁ , ₂ ,..., , )

n

f ( y ₁ , y ₂ ,..., y , t )

n n

(155)

dy n

dt

dy

dt

La matrice jacobienne de ce système s'écrira :

. ?

dy n ?

.... ?

?

df n

. ?

dy ? ?

n

df ?

1

(156)

df₁

1

dy

df n

1

dy

Pour laquelle on calculera les valeurs propres. Pour cette méthode, il faut intégrer sur une longueur importante à cause des dynamiques lentes, avec de petits pas en raison des dynamiques rapides. C'est une méthode inefficace et de fois infiniment longue.

2) Méthode de GEAR (ou BDF : backward differentiation formulas)

Par cette méthode, on cherche à interpoler la fonction y(t) grâce aux valeurs précédentes ( _yn+1, y_n, yn-1, yn-2, ,yn-k+1) avec un polynôme d'interpolation noté q(t). Il y' a donc une contrainte supplémentaire :

q'(tn+1)=f(tn+1)

c'est une méthode à pas d'intégration et ordre variables.

Pour k=1 :

y n+ 1 = y_n + h. f ( y n +1) (157)

Pour k=2 :

3 1

h

f y n + = y n + - y _n + y n - . ( ) 2 (158)
1 1
2 2 1
Pour k=3 :

11 3 1

h f y

. ( ) = y - +

3 y y - y (159)

n + 1 n + 1 n n - 1 n - 2

6 2 3

Pour k=4 :

25 4 1

h f y

. ( ) = y - 4 3

y y

+ - y + y (160)

n + 1 n + 1 n n - 1 n - 2 n - 3

12 3 4

Pour k=5 :

137 10 5 1

h f y

. ( ) = y - +

5 5

y y - y + y - y (161)

n + 1 n + 1 n n - 1 n - 2 n - 3 n - 4

60 3 4 5

Pour k=6 :

147 15 20 15 6 1

h f y

. ( ) = y - 6 y + y - y + y - y + y (162)

n + 1 n + 1 n n - 1 n - 2 n - 3 n - 4 n - 5

60 2 3 4 5 6

3) ODE 15s

Ce solveur est une amélioration de la méthode de GEAR. C'est une méthode à pas variable et ordre variable entre 1 et 6, avec une exactitude allant du bas niveau à un niveau moyen. On l'emploi généralement lorsque l'ODE45 est lent.

4) ODE 23s

Il permet la résolution des problèmes raides, avec un bas niveau d'exactitude. 4) ODE 23t

Il permet la résolution des problèmes modérément raides, avec un bas niveau d'exactitude.

5) ODE 23tb

Il permet la résolution des problèmes raides, avec un bas niveau d'exactitude.

2. Fichier parametresrobot.m

C'est un script dans lequel on affecte des valeurs aux différents paramètres du robot et aux entrées de la fonction dynamique_moteurCC. Comme ces entrées doivent varier dans le temps, la contrainte est qu'il faut qu'elles aient ( + 1 )

tfin valeurs, avec tfin qui est le temps d'intégration et

h

h le pas d'intégration. Pour saisir facilement ces entrées, nous allons générer 4 tranches de di ou di1 valeurs chacune, et ce, partant de leurs bornes et ensuite faire la concaténation de liste. Ce fichier est repris en annexe 3.

di = entier le plus proche de )

( h

tfin (163)

4 .

tfin

di 1 = -3* di+1 (164)

h

3. Fichier dynamiquemoteurCC.m

Les entrées sont les courants et les sorties, les couples moteurs. Après la déclaration des variables et différents paramètres du robot, la fonction parametres_robot est appelée et les couples sont calculés par la relation (94) et (95), pour finir par la visualisation de ces couples en fonction du temps.

Début

Déclaration des variables globales

Calcul de K, C1 et C3

Affichage des résultats

Fin

4 Fichier bouclerobot.m

Dans ce script, nous faisons le traitement dynamique et cinématique du robot. Il s'agit ici de trouver les angles de rotation de rotation des roues et les différentes réactions connaissant les couples appliqués aux moteurs, sortis de dynamique_moteurCC (traitement dynamique) et, des angles de rotation des roues, trouver les positions, les vitesses, les accélérations et l'orientation du robot. Nous avons été contraint de faire les deux traitements dans une même boucle par la non linéarité des équations (alpha dépend des ces angles). Ses temps forts sont :

· Déclaration des différents paramètres globaux ;

· Initialisation de la variable t, faisant office du temps dans les différents calculs, du compteur i et des conditions initiales ;

· Création des matrices de dimensions adéquates pour le stockage des différentes sorties ;

· Tant que t=120 secondes, les opérations suivantes seront exécutées :

o i=i+1 : actualisation du compteur ;

o Affectation de la valeur de C1(i) et C3 (i) aux couple de calcul C1c, C3c , valeurs à considérer dans les calculs au temps t ;

o Calcul des valeurs des réactions au temps t par les relations (80), (81), (82), (83), (84), (85), (86), (87), (88), (118), (119), (120), (121), (123), (124) et (125);

o Lancement de l'intégration de la dynamique avec le solveur ODE45 ; o Mémorisation de la valeur actuelle de yd dans la matrice sorties_d ;

o Mémorisation des valeurs des réactions dans des matrices respectives ; o Lancement de l'intégration de la cinématique avec le solveur ODE45 ; o Mémorisation de la valeur actuelle de yc dans la matrice sorties_c ;

o Calcul de alpha au temps t (alp) et de ses deux dérivées (dalp et ddalp) ;

o Mémorisation de la valeur actuelle de alp et dalp dans leurs matrices

respectives ;

o Mémorisation de la valeur actuelle de t dans la liste temps ;

o fin de la boucle

· Calcul des positions, vitesses et accélérations du robot ;

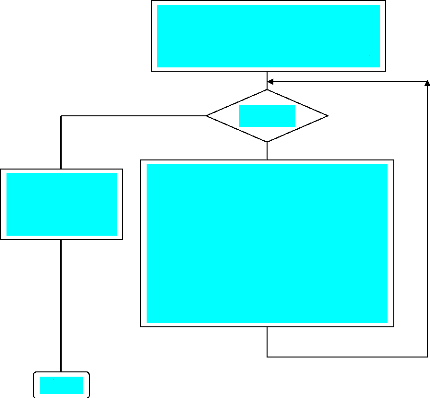
Calcul des positions, vitesses et

accélérations du robot.

Fin

i=i+1 ;

affectation des couples de calcul ;

calcul des réactions ;

lancement de l'intégration dynamique ; Mémorisation de la valeur actuelle de yd dans la matrice sorties_d ;

Lancement de l'intégration cinématique ; Mémorisation de la valeur actuelle de yc dans la matrice sorties_c ;

Calcul de alp, dalp et ddalp ;

t=t+h

mémorisation du temps ;

t=0 ;
i=0 ;
conditions initiales ;
création des matrices sorties_d et sorties_c ;

t=tfin-h

Le script possède 2 fonctions internes dans lesquelles les équations à intégrer{(5) et (6) pour la cinématique, (97) et (98) pour la dynamique} ont été définies. Son ordinogramme est le suivant :

Début

Déclaration des
paramètres du modèle

Appel des paramètres du robot et des entrées
du modèle

A l'instant initial, toutes les réactions sont nulles sauf R3, R6, R7, R11, R12, R14 et R16.Leurs valeurs sont obtenues en traduisant l'équilibre statique du robot (figures 5, 6, 7 et 8).

Mg l

.

R R mg

3 = = +

16 (165)

2 . ( )

l e

+

Mg l

.

R R

6 = =

¹¹ l e (166)

2 . ( )

+

Mg l r

. .

R R

= = (167)

7 ¹² 2 . ( )

l e

+

Mg e

.

R 14 l

e

= (168)

( )

+

5. Fichier robotmobile.m

Ce modèle a pour entrées les courants ia1 et ia3 et pour sorties les accélérations, les vitesses et les positions du robot (aG, vG et rG). Il a la structure suivante :

ia1 ia3

Dynamique moteur
CC

C1

C3

Dérivation

Dynamique robot

° è1

° è3

Cinématique robot

?

aG

á

?

rG

?

vG

L'ordinogramme du modèle est le suivant :