Chapitre I
Le Modèle
géométrique direct du robot (MGD)
I.1. Introduction
Un robot manipulateur se compose d'un ensemble de corps
reliés par des articulations, ces derniers peuvent être simples
« 1ddl » rotoïde ou prismatique, ou bien complexes,
« 2 ou 3ddl »une rotule ou un cardan. On suppose que toutes
les articulations ont seulement 1ddl, puisque une articulation complexe peut
être considéré comme une succession des articulations
simples avec des liaisons de longueur zéro, avec cette supposition,
l'action de chaque articulation peut être décrit par un nombre
réel simple : l'angle de rotation dans le cas d'une articulation
rotoïde ou le déplacement dans le cas d'une articulation
prismatique.
L'objectif du modèle géométrique direct
(MGD) est de déterminer l'effet cumulatif des variables articulaires,
dans ce chapitre nous développerons un ensemble de conventions qui
fournissent une procédure systématique pour calculer ce
modèle. Il est, naturellement, possible d'effectuer le MGD même
sans respecter ces conventions, mais pour un manipulateur de n
liaisons le MGD peut être extrêmement complexe et les conventions
présentées ci-dessous simplifient largement la
modélisation et donnent une langue universelle avec laquelle les
ingénieurs de la robotique peuvent communiquer [SPO 04].
I.2. Description de la
géométrie des robots à structure ouverte simple
Un robot manipulateur à structure ouverte simple avec
n articulations est composé de n+1 corps notés
 , puisque chaque articulation relie deux corps, nous numérotons
les articulations de 1 à n, et nous
numérotons les corps de 0 à n,
à partir de la base. On associe à chaque corps i du
mécanisme un repère orthonormé direct  noté . Les repères particuliers sont d'une part celui de la base  noté  et d'autre part  celui de l'organe terminal. Le repère de la base occupe une
position et une orientation connues par rapport à un repère fixe
noté Ratelier, si le robot est à un
poste fixe dans un atelier.
Le robot manipulateur pourrait lui-même être
mobile (par exemple, il pourrait être monté sur une plateforme
mobile ou sur un véhicule autonome), et il peut être
manipulé facilement en prolongeant légèrement les
techniques présentées ici [SPO 04].
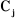
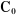
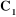
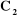
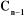
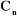
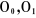
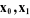
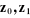
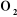
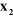
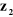
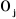
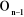
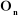
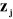
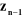
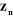
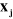
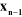
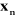
Figure I.1. La
chaîne cinématique d'un robot série
Dans la littérature il existe plusieurs méthodes
et notations pour la description de la morphologie des robots, les plus
répondues sont : [BEN 06]
· La méthode de Denavit-Hartenberg qui est
très bien adaptée pour les mécanismes à structures
de chaînes simples où toutes les liaisons sont
élémentaires, mais, elle présente des difficultés
lorsqu'il s'agit de mécanismes à structures de chaînes
complexes.
· La méthode de Khalil-Kleinfinger vient palier
les inconvénients cités précédemment, mais elle
présente des redondances pour les mécanismes à structures
de chaînes simples [FLÜ 98].
On ne s'intéresse ici qu'à la première
méthode puisque nous travaillons sur un robot à chaîne
ouverte simple.
I.2.1. Paramétrage de
Denavit Hartenberg
Les paramètres de Denavit et Hartenberg sont quasi
universellement adoptés par les roboticiens pour définir, avec un
nombre minimum de paramètres, les matrices de transformations
homogènes élémentaires qui permettent de passer du
repère associé à un corps du robot au corps qui le suit
dans la chaîne cinématique, les corps sont supposés
parfaitement rigides et les articulations sont considérées comme
idéales.
Un repère de référence  est assigné pour chaque corps  du robot à l'articulation i où elle
rencontre le corps précédent , ce repère est défini comme suit :
-- L'axe  se dirige le long de l'axe de l'articulation i.
-- l'axe  est aligné suivant la direction de la perpendiculaire
commune aux axes  et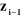
-- l'axe , non représenté sur la figure, est choisi de
manière à former un trièdre orthonormé direct
avec et  .
Les transformations élémentaires qui
permettent d'exprimer le passage du repère  au repère  (Figure I.2) sont :
· une translation di suivant
 égale à la longueur de la perpendiculaire commune.
· une rotation d'angle  autour de l'axe . est l'angle entre  et .
· une rotation d'angle  autour de l'axe . est l'angle entre l'axe xi-1 et l'axe .
· xj
zi-1
i
i
di
Oj
xi-1
zi
rj
Oi-1
une translation suivant l'axe . L'amplitude de cette translation, notée , est donnée par la distance (signée) entre l'axe  avec l'axe [GRE 05].
Figure I.2.
Paramètres de Denavit et Hartenberg
Il est à noter que les angles sont positifs quand la
rotation est dans le sens inverse des aiguilles d'une montre.
Les paramètres  sont les paramètres de Denavit et Hartenberg. On remarque que
seul quatre paramètres sont nécessaires pour passer d'un
repère  au repère , grâce notamment au choix de l'emplacement de ces derniers.
La variable articulaire  associée à la iième
articulation se traduit par la relation :
(I-1)
|
tel que :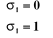
|
si l'articulation i est rotoïde
|
et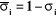 
|
(I-2)
|
|
si l'articulation i est prismatique
|
En terme de matrice de transformation homogène, les
quatre transformations élémentaires donnent la matrice
suivante :
 (I-3)
après son développement, on obtient :
(I-4)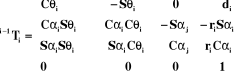 
avec :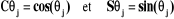 
la matrice de transformation homogène est souvent notée sous la forme :
 (I-5)
tel que :
 :est la matrice de rotation (3x3), appelé aussi matrice
d'orientation ou matrice des cosinus directeurs, elle représente la
rotation entre les deux repères  et , Les colonnes de la matrice  représentent les composantes des vecteurs unitaires du
repère  dans le repère  .
 est la matrice de position (3×1) qui définit l'origine du
repère  dans le repère  .
| 
