Liste des tableaux
Tableau I.1. Paramètres
géométriques relatifs au mécanisme
....................................11
Tableau II.1. Types d'équations
(Méthode de Paul) ................................................23
Tableau IV.1. Paramètres entrant dans le
calcul du modèle dynamique ......................... 62
Introduction Générale
Le problème de la commande d'un robot manipulateur peut
être formulé comme la détermination de l'évolution
des forces généralisées (forces ou couples) que les
actionneurs doivent exercer pour garantir l'exécution de la tâche
tout en satisfaisant certains critères de performance.
Différentes techniques sont utilisées pour la
commande des bras manipulateurs. La conception mécanique du bras
manipulateur a une influence sur le choix de schéma de commande. Un
robot manipulateur est une structure mécanique complexe dont les
inerties par rapport aux axes des articulations varient non seulement en
fonction de la charge mais aussi en fonction de la configuration, des vitesses
et des accélérations.
La plupart des robots utilisent des servomoteurs
électriques comme actionneurs. Les caractéristiques des
servomoteurs ont un rôle important pour la sélection du
système de commande.
Dans le cas où, les articulations sont
actionnées par l'intermédiaire de réducteurs à
forts rapports de réduction, l'inertie vue par les moteurs varie peu.
Dans ce cas, les asservissements peuvent être assurés axe par axe
par des boucles de commande classiques PID [TEC 07]. Ses avantages sont la
facilité d'implantation et le faible coût de calcul. En
contrepartie, la réponse temporelle du robot varie selon sa
configuration, on constate des dépassements de consigne et une
mauvaise précision de suivi dans les mouvements rapides [KHA 99].
En opposition, quand le robot utilise des servomoteurs avec de
faibles rapports de réduction, les boucles de commande doivent compenser
les effets des variations des forces d'inertie et de gravité fonctions
de la configuration. Les lois de commande basées sur les modèles
dynamiques des robots (appelée commande dynamique) donnent de
très bons résultats dans ce cas. Ils permettent de maintenir la
réponse dynamique du système dans certains critères de
performance. En utilisant ce type de techniques les robots peuvent
évoluer à grandes vitesses [AGU 07].
En effet la majorité des tâches confiées
aux robots sont délicates et exigent une très grande
précision sous des trajectoires rapides. Dans ce cas le type de commande
nécessaire est la commande par découplage non linéaire,
méthode qui est considérée comme la solution
théorique idéale pour la commande de ce type de robot [KHA 78],
[BEJ 85], [LUH 80],....
Notre travail porte sur la commande d'un bras manipulateur en
supposant que son application exige des évolutions rapides et une grande
précision et nous n'abordons pas sa construction.
Le schéma de commande que nous proposons n'utilise que
des capteurs proprioceptifs et reste ouvert pour l'inclusion de capteurs
extéroceptifs (systèmes de vision, capteurs d'effort, capteurs
tactiles,...) pour les boucles de commande de plus haut niveau. Le
schéma de la figure 1 présente cette idée de façon
simplifiée [SPO 04].
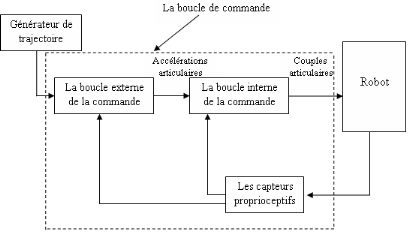
Figure 1.
Schéma hiérarchique de la commande.
La commande se fait soit dans l'espace opérationnel,
soit dans l'espace articulaire, le coût de calcul de la commande dans ce
dernier cas est quasiment égal au nombre d'opérations
nécessaires pour établir le modèle dynamique [KHA 99].
Ainsi, pour réaliser cette commande, on doit essentiellement disposer
d'un algorithme de calcul du modèle dynamique performant, deux
méthodes sont utilisées dans le cadre de ce travail.
Dans le cas où les modèles du robot sont
parfaitement connus, cette méthode de commande présente des
performances très satisfaisantes. Cependant, en pratique, cette
condition n'est pas simple pour un robot à plus de trois ddl, on doit
disposer d'un langage évolué, qui nous permet d'extraire les
expressions de tous les modèles nécessaires, sous forme
symbolique. Le logiciel Maple répond à ce critère.
Problématique :
L'objectif de ce travail est :
Ø l'élaboration de tous les modèles du
robot nécessaire à la commande : les modèles
géométrique, cinématique, et dynamique : directs et
inverses.
Ø trouver une loi complète de commande,
permettant de contrôler le mouvement du bras manipulateur, en tenant
compte de tous les problèmes qui surviennent lors du mouvement.
Durant notre travail on prend en considération les
suppositions suivantes :
Supposition 1
Le robot manipulateur utilisé est de type série
à 6 ddl de structure (RRPRRR), il est composé de corps
rigides.
Supposition 2
Tous les paramètres inertiels sont connus, on ne
s'intéresse pas à l'étape de l'identification de ces
paramètres.
Supposition 3
Les déformations non linéaires tels que les
frottements et les perturbations internes sont négligeables.
Supposition 4
Toutes les positions et les vitesses articulaires sont
mesurables.
Supposition 5
Nous avons supposé que le système et sa commande
sont continus. Dans la pratique, la commande étant
réalisée par calculateur (systèmes discrets).
Supposition 6
Les efforts extérieurs de l'organe terminal sur
l'environnement sont supposés statiques (donnés
aléatoirement), on ne tient pas en compte comment les
calculés.
Organisation du mémoire :
Ce mémoire est scindé en cinq chapitres et une
conclusion :
Dans le premier chapitre on présente la méthode
du calcul du modèle géométrique direct des bras
manipulateurs à structure ouverte simple. On applique la méthode
de Denavit Hartenberg pour représenter les transformations entre
repères, et les angles de Roulis Tangage Lacet pour la
représentation de l'orientation de l'effecteur dans l'espace
opérationnel.
Dans le deuxième on résout le modèle
géométrique inverse du robot, la solution retenue nous servira
à transformer la trajectoire opérationnelle suivie par le robot
en trajectoire articulaire correspondante.
Le troisième chapitre traite l'étude
cinématique du robot pour pouvoir calculer ses vitesses
opérationnelles à partir des vitesses articulaires et vice
versa. Dans ce chapitre, on voit aussi l'intérêt de la matrice
jacobienne et comment déterminer les positions singulières.
Le quatrième chapitre est dédié
à l'étude dynamique du robot permettant de calculer les couples
qui doivent être fournis par les actionneurs. Nous présentons deux
formalismes du calcul dynamique des bras manipulateurs puis on les applique au
robot pour déterminer ces couples.
Enfin, le dernier chapitre est consacré à la
commande du robot. Dans une première phase nous faisons un bref rappel
sur la commande classique PID, ensuit nous appliquons la loi de commande
dynamique dans l'espace articulaire, puis dans l'espace opérationnel.
Nous proposons des améliorations permettant de traverser les
configurations singulières sans divergences des résultats.
Dans la conclusion générale nous portons
un regard critique sur ce travail et nous finissons cet exposé par
quelques propositions.
| 


