· Application sur
le robot choisi
Pour valider la solution de Nakamura, sur notre travail, on a
donné une trajectoire qui passe par des positions singulières du
robot (Figure V.14)
 et 
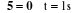
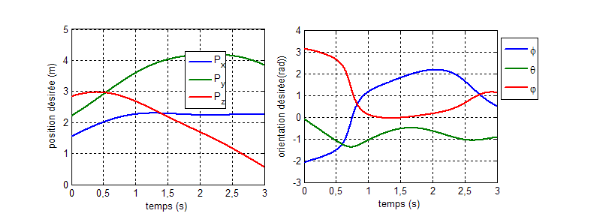
Figure
V.14. La trajectoire désirée
La figure (V.15) montre la position de
l'effecteur et les erreurs qui la correspondante, lors du passage par les
positions singulières choisis sans tenir en compte l'inverse
généralisée de la matrice jacobienne.
Au niveau de position opérationnelle; la valeur
maximale de l'erreur de translation est 6*10-3(m), et l'erreur de
rotation est de l'ordre de 10-2 (rad). Ces erreurs sont multiples
de 100 à 1000 fois des erreurs trouvées dans le cas d'une
trajectoire ne contient pas des positions singulières. Mais on peut dire
que le système converge.
Tandis qu'au niveau des coordonnées articulaires
mesurées, les valeurs des vitesses sont très grandes, de l'ordre
de 5000 rad/s. De même les positions articulaires dépassent ses
limites naturelles (2*pi rad), figure (V.16).
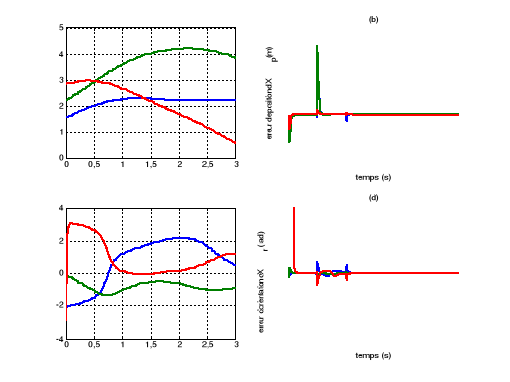
Figure
V.15. La position de l'effecteur et les erreurs de position
dans l'espace opérationnelle.
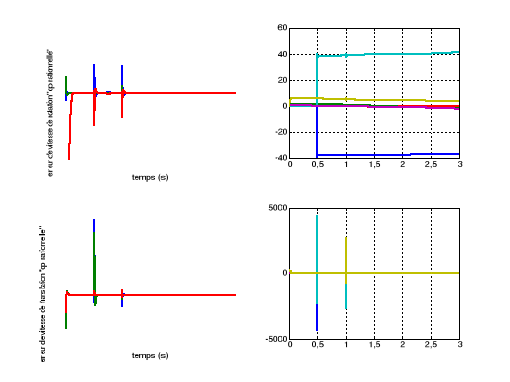
Figure V.16.
« à gauche » l'erreur de vitesse
opérationnelle
« à
droite » les positions et les vitesses articulaires
calculées.
On a fait le calcul de la matrice inverse
généralisée , avec , les résultats de simulation obtenus dans ce cas sont
montrés par les figures (V.17), (V.18).
On voit clairement que la commande au voisinage des positions
singulières, est très bien traitée par cette
solution.
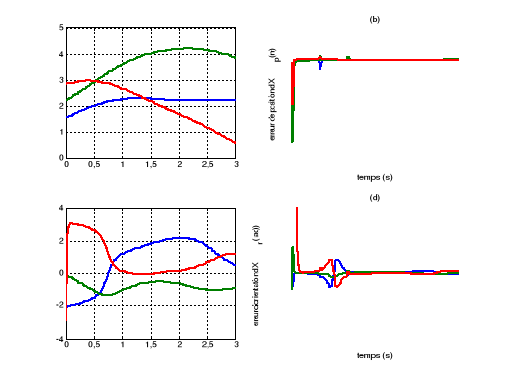
Figure V.17.
Le cas d'utilisation de l'inverse
généralisée.
La position de l'effecteur et les erreurs de
position dans l'espace opérationnelle
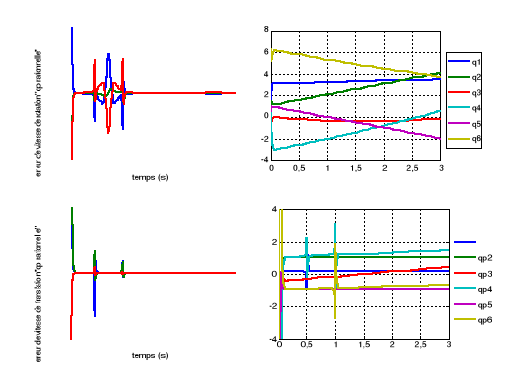
Figure
V.18. Le cas d'utilisation de l'inverse
généralisée.
« à
gauche » l'erreur de vitesse opérationnelle
« à
droite »les positions et les vitesses articulaires
calculées.
V.4. Conclusion
Dans ce chapitre, nous avons présenté la
synthèse de la commande dynamique d'un bras manipulateur rigide dans les
espaces articulaire et opérationnel.
C'est dans l'étape de validation des différents
schémas de commande que nous avons constaté l'importance des
modèles géométrique, cinématique et dynamique pour
le calcule des consignes de commande.
Nous obtenons un haut niveau de performance de la boucle
d'asservissement dans l'espace opérationnel, même en
présence de configurations singulières. L'utilisation de
l'inverse généralisée a permis de traverser les
configurations singulières sans problèmes.
Finalement, après toutes ces simulations, nous
obtenons un schéma de commande qui satisfait les contraintes du robot
choisi ; le repère référence est celui de l'atelier,
une vitesse grande , un effort extérieur statique et la connaissance
parfaite des paramètres inertiels et géométriques.
| 
