On suppose que les positions et vitesses articulaires
sont mesurables et que les mesures ne sont pas bruitées,
l'équation dynamique du robot peut s'exprimer sous forme
compacte :
(V-3)
où  et  les estimations respectives de M et
H.
alors, dans le cas idéal où le modèle
est supposé parfait, le système est régi par
l'équation :
 (V-4)
 peut être considéré comme un nouveau vecteur de
commande. On se ramène donc à un problème de commande de
n systèmes linéaires, invariants,
découplés et du second ordre (doubles intégrateurs).
On désigne respectivement par  l'accélération, la vitesse et la position
désirées dans l'espace articulaire, si le mouvement est
complètement spécifié, alors w(t) est
donné par la relation :
 (V-5)
où  et  sont des matrices constantes, diagonales et positives de dimension (n x
n).
(V-6)
avec :
 facteur d'amortissement
 : Pulsation propre
Pour un modèle parfait, l'évolution du vecteur
des erreurs articulaires
(V-7)
est régie par
l'équation :
(V-8)
Les erreurs articulaires sont découplées et
chacune se comporte comme un système du second ordre dont on peut fixer
la rapidité de réponse (choix de ) et l'amortissement (choix de , étant donné ), En général, on choisit un amortissement égal
à 1 pour avoir une réponse sans
dépassement [CRE 97]
Cette dernière équation a pour solution un
signal e (t) qui tend exponentiellement vers zéro. Le
système en boucle fermée, avec cette loi de commande, dans le cas
où le modèle du robot est connu avec exactitude, est
asymptotiquement stable. Le schéma bloc de cette loi de commande est
représenté sur la figure (V.2).
+
+
+
+
+
-
+
-
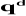
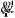
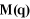
Robot
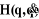
Kp
Kv
+
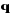
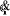
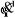
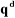
Figure V.2.
Commande dynamique pour un mouvement complètement
spécifié
Le signal de commande aux actionneurs comporte trois
parties :
· la première compense les couples et forces de
Coriolis, centrifuges, de gravité et de frottements (H)
· la deuxième est une correction de position et de
vitesse à gains variables représentée respectivement
par .
· La troisième constitue une anticipation des
forces d'accélération désirées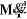 
Le modèle dynamique est calculé soit par le
formalisme de Lagrange soit par le formalisme de Newton Euler, dans ce dernier
cas le  est calculé explicitement, on n'a pas besoin de calculer
séparément le M et le H, sauf
lors de la simulation du comportement du robot (le calcul du MDD).
· Application sur le
robot choisi
Afin de montrer l'apport de cette technique de commande, une
simulation numérique a été effectuée sur le robot
choisi. On a considéré une trajectoire de référence
complètement spécifiée assurant une continuité en
position, vitesse et accélération.
L'effet extérieur sur l'organe terminal est tenu en
compte fe, les efforts extérieurs sur les
autres corps du robot sont supposés nuls, les frottements sont
négligeables sur toutes les articulations.
fe =[20,20,20,12,30,25]T
Le modèle dynamique du robot est calculé par
l'un des deux formalismes décrits précédemment.
Pour la simulation du robot on a utilisé le
modèle dynamique direct, (IV-36) en suite on a
intégré; le  pour trouver  et cette dernière pour trouver .
Les valeurs des paramètres des contrôleurs ont
été réglées selon les formulations
présentées précédemment. Les lois de commande ont
été testées en simulation dans l'environnement
Matlab/Simulink®.
· Réglage du PID
D'après les équations vues dans le paragraphe
V.2, les paramètres nécessaires pour
régler la commande PID d'une articulation, sont la fréquence  et la valeur de .
Après le calcul nécessaire, les valeurs de  trouvées sont données par :
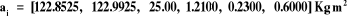
Les valeurs calculées et ajustées des gains, lors
de la simulation, sont :
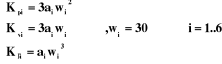
· Réglage de la commande
dynamique
De la même façon, les valeurs à choisir pour
régler la commande dynamique sont la pulsation  et le facteur d'amortissement , selon l'équation (V.6) et après
ajustement en simulation, les valeurs de gains sont fixées à:
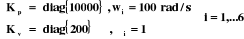
Nous avons utilisé deux tests séparés,
l'un utilise la commande PID et l'autre utilise la commande dynamique.
La figure (V.4) montre le comportement
du robot, pour les deux tests, en poursuite de la trajectoire
présentée par la figure (V.3.a).
Les résultats de simulation montrent un meilleur
comportement de la commande dynamique par rapport à la commande PID,
L'erreur de position est de l'ordre de 10-5(rad) pour la commande
dynamique, et elle est de l'ordre de 10-3(rad) pour la commande PID.
De même, l'erreur de vitesse est voisine de
10-5(rad/s) pour la commande dynamique, et elle est de l'ordre de
10-3(rad) pour la commande PID.
On voit bien, « figure (V.3.c,
d) », que les couples / force donnés par
l'application des deux lois de commande, sont les mêmes,
ce qui nous amène à dire que pour les deux cas de
commande le système converge, mais avec une grande précision pour
la commande dynamique par rapport à la commande PID.
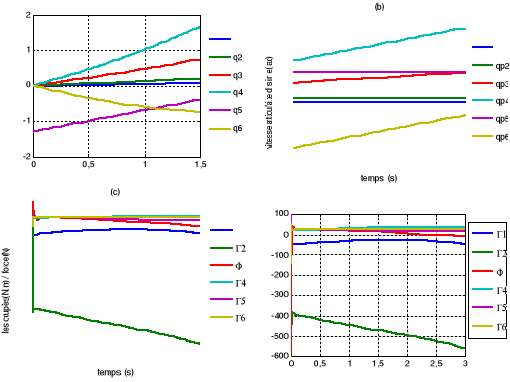
Figure
V.3. (a) positions articulaires (b) vitesses articulaires
(c) la commande PID
(d) la commande dynamique
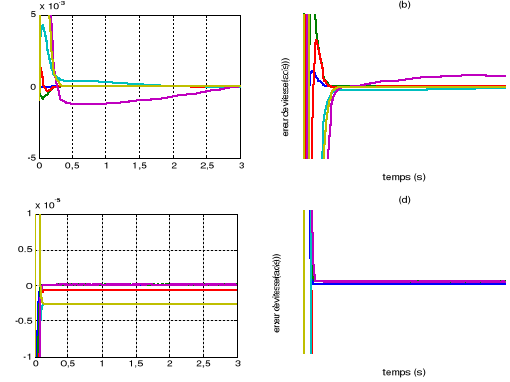
Figure V.4.
L'erreur de position et de vitesse
(a)et (b) la commande PID
(c) et (d) la commande
dynamique.
En suite on a répété le même travail,
pour une trajectoire caractérisée par des grandes vitesses
articulaires figure (V.5)
On voit bien que le système lorsqu'il
est contrôlé par la commande dynamique reste toujours stable,
contrairement au cas de la commande PID, qui est malgré qu'au
début du mouvement (t=[0, 2.5s]) le système est un peut stable
(figure (V.6.a, b)), mais il a divergé
complètement à l'extérieur de cet intervalle.
La divergence du système dans ce dernier cas, est
justifié, par le fait que la matrice d'inertie M(q)
n'est pas diagonale et dépend fortement de la configuration
q. De plus, aux grandes vitesses, les forces centrifuges et de
Coriolis « vecteur C(q) » peuvent
être importantes.
Pour ces raisons, l'utilisation d'asservissements
linéaires classiques conduit à des performances de
rapidité et de précision inconstantes et difficiles à
estimer étant donné le caractère fortement non
linéaire du processus commandé. Cet inconvénient est
notablement réduit par le schéma de la commande dynamique du
mécanisme (figure (V.6.c,d)).
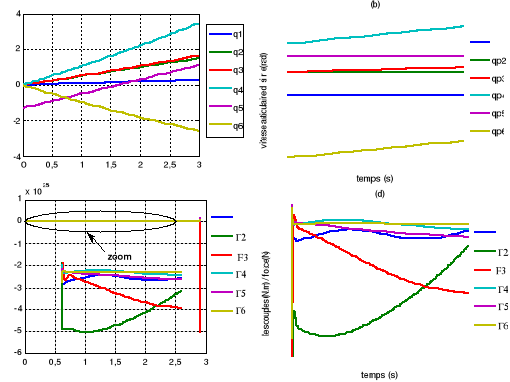
Figure
V.5. (a) positions articulaires (b) vitesses articulaires
(c) la commande PID
(d) la commande dynamique
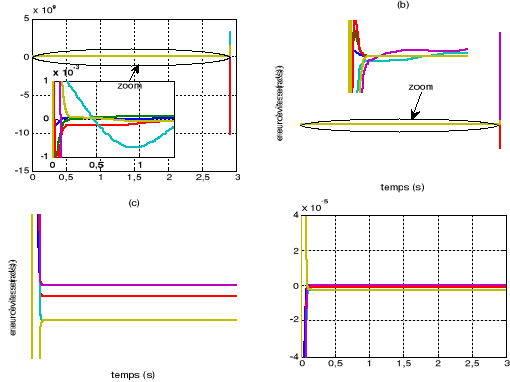
Figure V.6.
L'erreur de position et de vitesse
(a)et (b) la commande PID
(c) et (d) la commande
dynamique.
V.3.2.Commande dans l'espace opérationnel
Le problème de l'asservissement dans l'espace
cartésien pour un bras manipulateur, consiste à produire des
consignes capables de réaliser le mouvement opérationnel [AGU
07], une des deux solutions suivantes peut être choisie pour
réaliser la commande par découplage non linéaire :
V.3.2.1. Commande dans l'espace
opérationnel avec correction dans l'espace articulaire
Dans ce cas, on transforme le mouvement défini dans
l'espace opérationnel en un mouvement dans l'espace articulaire, puis on
met en oeuvre la commande dans l'espace articulaire du
§V.3.1. Le signal d'erreur est exprimé alors dans
l'espace articulaire [VIV 04].
On utilise le MGI pour trouver les variables articulaires
désirées, puis avec une procédure numérique on
dérive ces dernières pour obtenir la vitesse et
l'accélération (Figure V.7).
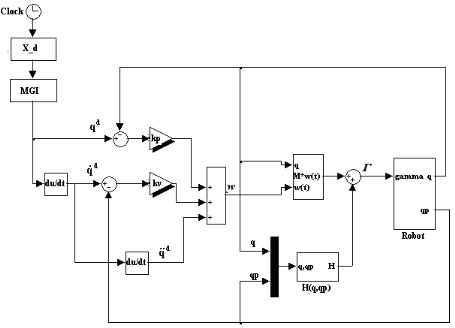
Figure V.7.
Commande dans l'espace opérationnel avec correction dans l'espace
articulaire
| 
