à‰tude des différentes lois de commande pour un robot manipulateur à 6DDL comportant une liaison prismatique

III.4.2. calcul de la jacobienne analytique

Puisque la rotation est spécifiée par les angles de RTL, les vitesses sont calculées par la relation. Un programme de vérification a été fait, toujours afin de valider les résultats, il est indiqué par le schéma présenté ci dessous :

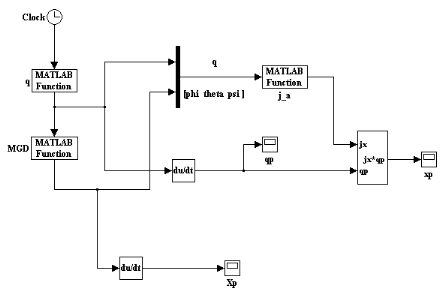
Figure III.4. Description du programme utilisé pour la validation de la jacobienne analytique

Les valeurs de q et X sont les mêmes que ceux de la section précédente.

Les résultats de la simulation du programme (Figure III-5), interprètent la validité de la jacobienne analytique utilisée et donc le modèle cinématique calculé.

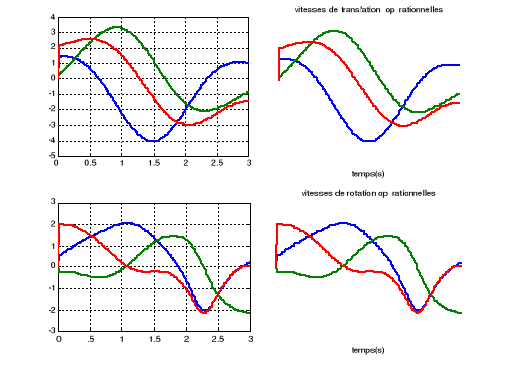
Figure III.5. Les vitesses opérationnelles par l'utilisation de la jacobienne analytique

III.4.3. Les positions de singularité 

Les positions singulières (Figures III-6.a, b et c ) sont les solutions de l'équation :

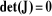
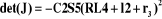
La résolution de cette équation donne les positions singulières suivantes : 

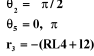
La singularité (figure III-6.a), correspond à une configuration dans laquelle le centre du poignet est confondu avec l'axe z₀ et le robot est en extension maximale (singularité d'épaule).

Pour , les deux articulations commandant et ont leurs axes confondus et le poignet se plis sur lui-même lorsque (figure III-6.b) , ce qui fait perdre un degré de liberté au robot . Dans cette configuration le modèle cinématique ne permet pas de commander une rotation autour de la normale au plan contenant les axes 4,5 et 6 (singularité du poignet).

Lorsque, le centre du poignet est confondu avec le point O₂ (figure III-6.c), mais c'est impossible de tomber dans ce cas puisque est toujours positive (articulation prismatique).

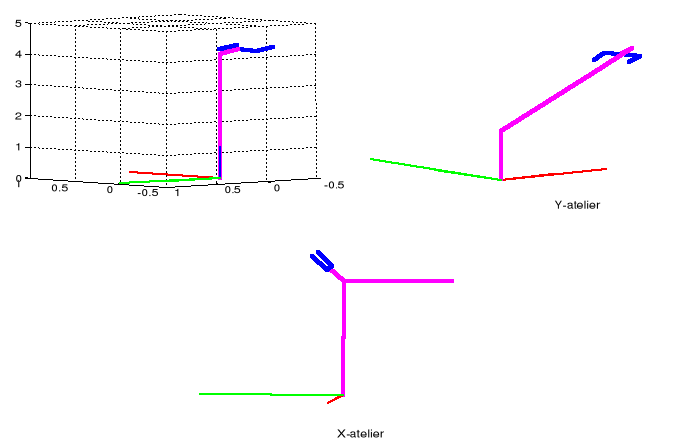
Figure III.6. Quelques positions singulières du robot