2.1.2.2. Frontière
déterministe et paramétrique
Farrell (1957) fut aussi à l'origine de l'approche
déterministe et paramétrique. Il proposa l'approximation de la
fonction de production efficace par une forme fonctionnelle connue à
priori. Il utilisa la forme fonctionnelle Cobb-Douglas pour illustrer
l'utilisation de cette approche sur des données agricoles de 48
États américains, tout en imposant des rendements constants
à l'échelle.
À la Figure 4, l'entreprise située au point D et
qui voudrait conserver un niveau d'utilisation U=1 des intrants pourrait
opérer au point C. Ainsi son niveau de production passerait de
YD à YC. Cependant, l'efficacité technique
peut être aussi mesurée en regard de l'utilisation des intrants.
En effet, il serait également possible de minimiser
l'utilisation des intrants pour un niveau de production donné,
c'est-à-dire produire le même extrant YD avec moins
d'intrants, soit U1 à la Figure 4. Cela placerait l'entreprise au point
B au lieu de D.
Figure 4 : Les deux types
de mesure de l'efficacité technique
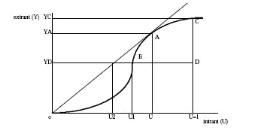
Source : Forsund, F. R. et L. Hjalmnsson
(1979).p.297
2.1.2.3. Frontière
stochastique
Les approches non paramétriques et paramétriques
discutées précédemment permettent la
détermination d'une fonction frontière
déterministe partagée par toutes les firmes, c'est à dire
que toutes les firmes partagent un mode de production commun et leurs
performances respectives sont comparées à la même
frontière de production. De plus, tout écart que les firmes
affichent par rapport à la frontière est totalement
attribué à de l'inefficacité. Cette notion de
frontière déterministe néglige la possibilité que
la performance d'une firme puisse être affectée par plusieurs
facteurs hors de son contrôle, tels les aléas climatiques, le
mauvais rendement des machines ou encore les pénuries des intrants, dont
l'effet est aussi important que les facteurs contrôlables par la firme.
Ces arguments sont à l'origine du développement de l'approche
stochastique ou d'erreur composée, initialement proposée par
Aigner, Lovell et Schmidt (1977), Meeusen et Van Den Broek (1977), et
améliorée par Jondrow et al. (1982) pour permettre l'estimation
d'indices d'efficacité technique spécifique à chaque
firme. Cette approche postule que le terme d'erreur est composé de deux
parties indépendantes, soit une composante purement aléatoire (V)
qui se trouve dans n'importe quelle relation et qui se distribue de chaque
côté de la frontière de production, et une composante
représentant l'inefficacité technique (U) et qui est
répartie d'un seul côté de la frontière.
La Figure 5 illustre les différences entre la
frontière de production déterministe et la frontière de
production stochastique dans le cas de deux firmes « i » et « j
». Ces deux firmes utilisent les quantités d'intrants Xi et Xj,
pour produire, respectivement, les extrants Yi et Yj. On constate que, pour la
firme « i », le niveau de production Y*i , qui correspond à la
frontière stochastique f(Xi) exp(Vi), est supérieur à Yi =
f(Xi), soit le niveau de production obtenu lorsque la frontière est
déterministe. Cela est probablement dû au fait que cette firme n'a
pas fait face à des conditions défavorables hors de son
contrôle, c'est-à-dire que le terme d'erreur aléatoire Vi
est positif. Par contre, pour la firme « j », le niveau d'extrant
stochastique Yj* est inférieur au niveau de production
déterministe Yi, suggérant que Vj est négatif. Dans les
deux cas, la production observée est inférieure à la
production frontière. Comme le souligne Battese (1992), il est possible,
selon la méthode de fixation de la frontière déterministe
préconisée, que la production observée Y et la production
frontière stochastique Y* = f(X) exp(V), se situent au dessus de la
production indiquée par la frontière déterministe f(X).
Figure 5 : La
frontière stochastique de production
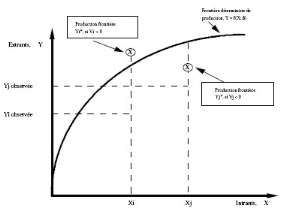
Source : Battese, 1992 : 191.
Cependant, et tel que mentionné par Forsund, Lovell et
Schmidt (1980), cette approche, dans sa version initiale, ne permet pas de
différencier les deux composantes pour chaque observation. Elle ne
permet que de calculer la moyenne du niveau d'efficacité pour tout
l'échantillon. Jondrow et al. (1982) ont montré qu'en assignant
à priori des distributions connues aux deux composantes du terme
d'erreur, il est possible de les différencier et d'obtenir une mesure de
l'efficacité pour chaque observation.
| 


