Evaluation de l'efficience technique des exploitations riricoles du périmètre irrigué de mission-tové

2.1.2. Les approches d'estimation de la frontière d'efficacité

Pour mesurer l'inefficacité, il faut établir une frontière de production. Concernant la frontière de production, qui est de loin la plus utilisée, la littérature distingue deux grandes approches selon la façon dont elle est estimée. Il s'agit des approches à frontières déterministes et des approches à frontières stochastiques. Les approches pour estimer les frontières déterministes sont pour leur part de deux types : paramétrique et non paramétrique. Les approches paramétriques attribuent une forme fonctionnelle particulière à la fonction de production. Aucune forme fonctionnelle n'est attribuée aux frontières par l'approche non paramétrique.

2.1.2.1. Frontière déterministe et non paramétrique

L'approche de la frontière non paramétrique fut introduite par Farrell (1957). Cette frontière, généralement de type déterministe, n'est pas liée à une forme fonctionnelle et l'isoquant frontière est estimé par les ratios intrants/extrant de chaque firme. L'isoquant convexe qui reflète la fonction de production efficace est ainsi construit à partir d'un nuage de points de sorte qu'aucune observation ne se situe ni à gauche ni au dessous de cet isoquant (Figure 2).

Cette façon de mesurer l'efficacité technique des unités de production est définie dans un contexte où la technologie de production est caractérisée par des rendements d'échelle constants.

Cependant, cette hypothèse est très restrictive. En effet, en cas de déséconomie d'échelle, la Figure (3 a) montre qu'un segment rejoignant deux points situés sur S est probablement inefficace, ce qui n'est pas forcément vrai en cas d'économie d'échelle alors que la courbe S est convexe (Figure 3 b).

Figure 2 : Détermination de la frontière d'efficacité technique selon Farrell

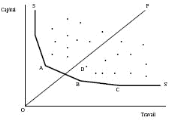
Source: Farrell, M. J., p. 256

Figure 3 Impact de l'économie et de la déséconomie d'échelle sur les mesures de l'efficacité technique de Farrell

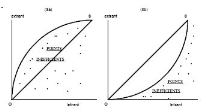
Source: Farrell, M.J, p.258.

Le modèle proposé initialement par Charnes et al. (1978) suppose ses rendements d'échelle constants (CRS model). Plus tard, Banker et al. (1984) ont proposé un modèle qui permet de relâcher cette hypothèse. Il s'agit du modèle des rendements d'échelle variables (VRS model).

Ces deux modèles sont présentés, de façon succincte, dans les paragraphes suivants.

2.1.2.1.1. Le modèle CRS (Constant Returns Scale)

Du point de vue théorique, selon Kalaitzandonakes et al.,(1992), pour une firme « i », mesure de l'efficience technique peut être obtenue par le modèle de programmation mathématique suivant :

Max Y_i / X_i

,

s. c. Y_j / X_j 1 pou j = 1, 2, ..., K (1)

où et sont les vecteurs des coefficients à estimer et Y_i et X_i renvoient, respectivement, aux vecteurs d'extrants et d'intrants de la firme « i ».

Ce problème maximise, pour chaque firme, le ratio extrant virtuel / intrant virtuel, tout en le contraignant à ne pas dépasser 1. Ainsi, toutes les firmes de l'échantillon sont forcées à se situer sur ou au dessous de la frontière d'efficacité.

Tel que résumé par Kalaitzandonakes et al. (1992), soit d'abord un échantillon de K firmes où chaque firme utilise M intrants pour produire N extrants différents. Le ratio entre l'extrant fictif et l'intrant fictif pour une firme constitue une mesure de son niveau d'efficacité technique. Cette partie sera développée plus loin dans ce document.

2.1.2.1.2. Le modèle VRS (Variable Returns Scale)

Comme mentionné par Coelli et al. (1998), la supposition des rendements croissants d'échelle est seulement appropriée quand toutes les firmes opèrent à une échelle optimale. La concurrence imparfaite, les contraintes de finance etc..., peuvent entraîner une firme à ne plus opérer à une échelle optimale (Coelli et al., 1998 : 150). Banker et al.(1984), ont été les premiers à proposer le modèle VRS qui n'est en fait qu'une extension du modèle CRS mais qui tient compte des situations où les rendements à l'échelle ne sont pas constants. L'application du modèle CRS originel, lorsque les firmes n'opèrent pas toutes à une échelle optimale, conduit à des mesures de l'efficacité qui confondent l'efficacité technique et l'efficacité d'échelle.