Evaluation de l'efficience technique des exploitations riricoles du périmètre irrigué de mission-tové

3.3.1.2. La forme transcendantale logarithmique de la fonction de production (Translog)

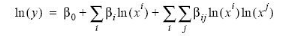
La forme générale de cette fonction suggérée par HEUYER  et al., (2004) est la suivante :

y, la production et xi, les facteurs de production

â_{i ,} les paramètres des termes linéaires,

Â_ij, les paramètres des termes d'interaction,

ln, logarithme népérien.

Elle mesure les interactions entre les variables indépendantes. Les paramètres â_i, Â_ij, Â_o seront estimés à l'aide du logiciel EVIEWS 3.1. Il permet de calculer les termes d'erreur u_i et v_i dont u_i est liée à l'inefficience technique et qui servent à déterminer deux autres paramètres important dans l'interprétation de l'efficience. Ces paramètres sont :

ó² = ó²_u + ó²_v et ë = ó²_u / ó²

ó² et ë représentent respectivement la variance du terme d'erreur global ( u + v) et le ratio de la variance du terme d'inefficience u sur la variance totale des termes d'erreur. Le paramètre ë permet de tester si la frontière stochastique de la fonction de production est préférable à celle estimée par la méthode des moindres carrés ordinaires. Ainsi dans l'incapacité de rejeter l'hypothèse nulle ë = 0 on conclura que la variance du terme d'erreur d'inefficience est nulle et le terme stochastique d'inefficience sera soustrait de l'équation réduisant la spécification des paramètres du modèle qui peut être estimé par la méthode MCO (KINTCHE, 2004).

Malgré les avantages de la fonction Translogarithme, la fonction Cobb-Douglas sera utilisée comme une première approximation compte tenu des moyens financiers limités et de l'absence de formation en économétrie.

3.3.2. Evaluation du modèle économétrique

L'évaluation portera sur chacun des paramètres du modèle puis sur le modèle global.

3.3.2.1. Tests de détection et correction

Ø Auto- corrélation

L'auto- corrélation résulte de la violation de l'hypothèse de l'indépendance dans le temps des éléments aléatoires. Elle n'apparaît que dans les séries en coupe longitudinale. Pour mesurer l'auto - corrélation des éléments aléatoires l'on peut effectuer un test visuel soit utiliser le test de Durbin Watson (GRELLET, 2003).

Etant donné que dans notre étude les données seront collectées en coupe transversale, paramètres retenus seront soumis à un test diagnostic préalable par rapport aux hypothèses du modèle classique sur l'hétéroscédasticité et la multicolinéarité.

Ø Hétéroscédasticité

Etymologiquement le mot hétéroscédasticité signifie dispersion ou variance différente. L'on dira que l'élément aléatoire connaît une hétéroscédasticité quand sa variance présente de larges écarts dans le temps. Il existe alors un biais important dans l'estimation des paramètres puisque toutes les observations n'ont pas le même poids dans l'estimation de Y. Elle provient de biais de spécification dans le modèle (GRELLET, 2003).

Pour déceler l'existence de l'hétéroscédasticité l'on utilisera soit un test visuel, le test de

Goldfield - Quandt, le test de Wite, le test de Breusch et Pagan, le test de Park etc... (IYOHA, 2004).

Dans notre étude on utilisera le test de Goldfield - Quandt suggéré par IYOHA,( 2004).

Il consiste à scinder l'échantillon en deux parties égales en omettant c observations au milieu de l'échantillon. Ensuite l'estimation par les MCO du modèle sur les deux échantillons composés chacun de (n - c)/ 2 observations permet de calculer les résidus pour les deux régressions soit :

S C R (1) = ?(e₁ )² et S C R (2) = ?(e₂ )²

Avec respectivement (n - c)/ 2 - k degré de liberté. n = nombre total d'observations ; k = nombre de paramètres à estimer. Enfin on calcule le ratio

R = S C R (2) / S C R (1).

Si les termes d'erreur sont normalement distribués alors R suit la distribution de Fisher

F [(n - c)/ 2 - k, (n - c)/ 2 - k]. Lorsque R est inférieur à la valeur tabulaire, l'hypothèse d'hétéroscédasticité est rejetée. Il est important de rappeler que ce test ne s'applique qu'aux échantillons de taille supérieure à 30 et pour définir c il est conseillé d'enlever le 6^ème des observations. Selon Gujarati (1998) l'erreur de l'équation d'estimation est systématiquement hétéroscédastique. Donc pour corriger ce problème, l'on peut diviser les observations de Y par leur écart type de sorte que quand l'écart type est élevé la pondération est faible et l'on peut utiliser les MCO. On peut aussi corriger ce problème en utilisant directement l'estimateur des moindres carrés généralisés (MCG).

Ø Multicolinéarité

La multicolinéarité dans un modèle économétrique indique l'existence des relations entre deux ou plusieurs variables indépendantes du modèle. Elle apparaît en cas de violation de l'hypothèse de caractère non stochastique des variables exogènes. Elle est parfaite lorsque qu'il y'a pas de terme d'erreur dans la relation de combinaison linéaire entre ces variables indépendantes ; Par contre, dans le cas contraire elle est imparfaite. La multicolinéarité est soupçonnée lorsqu'on observe des t-ratio non significatif et le coefficient de détermination R² élevé. Ceci est confirmé par la règle de KLEIN : le coefficient de corrélation partielle est plus élevé que le coefficient de détermination multiple R² (LARE-LANTONE ,2003). Généralement, on estime qu'un coefficient de corrélation partielle de valeur absolue supérieure à 0,8 est signe de multicolinéarité entre les variables concernées (Daré, 2004).

Cadoret et al, (2004), rappelle qu'en cas de multicolinéarité : (i) les variances estimées de certains paramètres ainsi que les coefficients de détermination sont très élevés (ii) les paramètres estimés sont très instables et montre de fortes variations lorsque de petites variations sont effectuées sur les observations et (iii) les signes des paramètres estimés sont parfois incorrects. Elle est corrigée par exclusion de certaines des variables corrélées ou leur combinaison ou une augmentation de la taille de l'échantillon. Mais il s'avère nécessaire quelque fois de ne rien faire lorsque les variables sont importantes pour l'estimation (Bourbonnais, 1998).