3.3.2..2. Mesure de la
qualité de l'ajustement
Les résultats obtenus par la MCO peuvent être
évalués statistiquement par les mêmes outils à
savoir : le ratio de Log-likihood et le R2 de Mc
fadden
Ø Le ratio de Log-likihood.
Encore appelé ratio de vraisemblance, il mesure la
qualité de la relation entre la variable endogène et les
variables exogènes. Ce ratio est donné par la par (Judge et al.,
1993 cité par KINTCHE, 2004) :
ë = 2 (LogIm -
LogIo)
où ë est le ratio de
vraisemblance ; Im représente la valeur
maximale du log de la fonction de vraisemblance et
Io sa valeur lorsque tous les coefficients sont
supposés nuls sauf la constante. Enfin il est distribué comme une
variable aléatoire de khi-deux de k-1 degré de liberté.
Les seuils de significations recherchés sont 0,5 % et 0,1%.
Ø Le coefficient de détermination multiple
de Mc Fadden, R2
Il est compris entre 0 et 1 et mesure la proportion de la
variabilité de la variable dépendante qui est expliquée
par les variables indépendantes contenues dans le modèle. Il
indique la qualité du modèle.
R2 est donné par la
formule suivante (Giraud, 1994) :
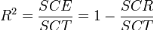
L'ajustement est d'autant meilleur que
R2 est voisin de 1.
Si R2 est un indicateur pertinent, il
présente un défaut parfois ennuyeux, il a tendance à
mécaniquement augmenter à mesure qu'on ajoute des variables dans
le modèle. Le R2 croît avec le nombre
de variables explicatives même si ces variables n'ont rien avoir avec le
phénomène étudié. Pour pallier cet
inconvénient, certains auteurs ont conseillé dans d'utiliser le
coefficient de détermination ajusté qui est corrigé des
degrés de liberté et notée 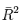 (Doucouré, 2005) : (Doucouré, 2005) :
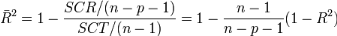
Où n = taille de l'échantillon et
p le nombre de paramètre à estimer.
3.3.2..3. Validation de
modèle économétrique
Deux tests permettent de valider le modèle
économétrique, ce sont : le test de Student et le test de
Fisher.
Ø Le test de Student
Il mesure la significativité individuelle des
paramètres estimés. On formule deux hypothèses :
Ho : a = 0 et H1 : a ? 0 que l'on testera.
On calcule la statistique (Doucouré, 2005) :
tcal = âk /
óâk
Où
tcal = le ratio de tudent
âk =
l'estimation de a
óâk =
l'estimation de l'écart type du coefficient a.
tcal est
distribué suivant la distribution de Student à n - k degré
de liberté.
Si |tcal | > t
á/2(n-k) tabulaire, alors l'hypothèse Ho est
refusée au seuil de á et le coefficient peut être
considéré significativement différent de 0. Ce test est un
tes de base qui a pour but de vérifié que la variable explicative
concernée influence la variable endogène. La non rejet de Ho
signifie que la variable explicative n'explique pas celle endogène.
Ø Le test de Fisher
Il teste l'existence de relation linéaire significative
entre les variables indépendantes prises ensemble et la variable
dépendante. On calcule le ratio suivant (Iyoha, 2004) :
Fcal = R2(n-k) / (1- R2
)(k-1).
Si le F calculé est supérieur à la valeur
tabulaire F[k-1,n-k] au seuil de á, on accepte l'hypothèse que
les paramètres estimés de la régression ne sont pas tous
nuls et que la statistique de R2 diffère significativement de
zéro. Cependant dans le cas contraire on accepte l'hypothèse que
les paramètres estimés de la régression sont tous nuls et
que la statistique de R2 ne diffère pas significativement de
zéro.
| 


