Construction d'un modèle prédictif basé sur le réseau de neurones profond pour la détection de cancer de la peau

Conclusion partielle.

Dans ce chapitre, nous avons présenté l'apprentissage automatique et l'apprentissage profond. Nous avons d'abord commencé par la description de l'apprentissage automatique et ses différentes architectures proposées. Ensuite, nous avons passé à la description de l'apprentissage profond.

Dans cette démarche, nous avons décelé les caractéristiques de l'apprentissage artificiel, entre autres : adaptation, généralisation, reconnaissance, amélioration et intelligibilité. Ce sont les cinq (5) caractéristiques qu'on peut trouver dans le modèle de machine Learning.

Etant atteints, les objectifs fixés pour ce chapitre, nous aborderons dans le second chapitre, l'une de méthodes de l'apprentissage supervisé qui est le réseau de neurones artificiels précisément le réseau de neurones à convolution ( Convolutionnal Neural Network, en anglais) spécialisé dans le traitement d'images, la reconnaissance de formes, etc. Il fait partir de Deep Learning (Apprentissage Profond, en français).

P a g e | 31

Chapitre deuxième : Réseau des neurones à convolution (CNN).

2.1. Introduction.

Les réseaux neuronaux convolutionnels CNNs « Convontoinal neurone network » sont un type spécialisé de réseau neuronal pour le traitement de données qui a une topologie connue, ils sont des réseaux supervisé et non supervisé, cela dépend de l'exigence et l'utilisation, cependant, principalement sont supervisé (Patterson et al., 2017).

L'informaticien japonais « Kunihiko Fukushima » a jeté les bases du lancement de cette structure par son travaille sur Neocognitron en 1980 (Vázquez, 2018).

Comme une grille, ils appartiennent aux réseaux de neurones artificiels acycliques, le nom convolutionnel indique que le réseau emploie une opération mathématique appelée convolution, et cela signifie un type spécialisé d'opération linéaire (Goodfellow et al., 2016).

Un réseau de neurones convolutif (CNN) s'inspire du cortex visuel des mammifères afin d'analyser une image en profondeur. Cette architecture a été introduite par le chercheur "Yann Le Cun" Dans les années 90.

Dans ce chapitre, nous introduirons le réseau de neurones convolutif et les différents algorithmes qui le distingue d'un réseau de neurones classique (DNN⁶).

2.2. Motivations des réseaux de neurones convolutifs. Les principales motivations des CNN sont les suivantes :

A Un Deep Neural Network (DNN) profond pour analyser une images complexe dégrade rapidement. Il faut trouver une méthode moins coûteuse et plus intuitive afin de faire du traitement d'image en général et la détection de forme en particulier.

A Une image est composée de sous éléments, il faut donc exploiter cette hiérarchisation avec une détection de formes plus granulaire.

A Les positions, tailles, couleurs..etc sont compliqués à extraire pour les réseaux classiques afin d'avoir une compréhension générale de l'image.

A Réduire la dimensionnalité des paramètres d'un Deep Neural Network (DNN) classique et celle des images.

⁶ DNN : Dense/Deep Neural Network

P a g e | 32

? S'inspirer de la biologie afin de créer une intelligence artificielle fut un succès, se tourner une seconde fois vers elle afin de modéliser une nouvelle IA⁷ peut être fructueux.

2.3. Le cortex visuel.

Dans la définition suivante, à chaque étape, nous citerons entre parenthèses une notion analogue à celle des CNN.

L'oeil perçoit la lumière (image en entrée) à travers la pupille puis véhicule l'information vers le cortex visuel qui se situe derrière la tête. Cette information est sous forme de signaux électriques dont la fréquence correspond à une information codée (convolution). Au cours de leurs trajets, les informations passent d'une fibre nerveuse à une autre grâce aux synapses (connexion de neurones). Le cortex visuel est constitué de plusieurs aires spécialisées dans le traitement des messages nerveux (les filtres). Selon la fréquence des signaux électriques émanant de l'information, chaque air interprète une caractéristique de l'image comme suit (cartes de caractéristiques) (Maxicours, 2021).

Figure 9. Les différentes aires du cortex visuel. 2.4. CNN et structure générale.

Construire un CNN revient à superposer plusieurs couches de manière hiérarchique, chacune d'entre elles calcule une représentation abstraite de l'image au fur et à mesure (Nguyên, 2018). L'opération se présente en général de la manière suivante.

⁷ IA : Intelligence Articielle

P a g e | 33

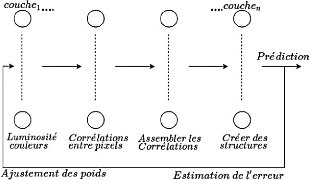
Figure 10. Structure générale d'un CNN.

2.5. CNNs et fonctionnement.

Le fonctionnement de CNNs est inspiré à partir du fonctionnement du processus biologique, ils consistent en un empilage multicouche de perceptrons, dont le but est le prétraitement de petites quantités d'informations (Patterson et al., 2017).

Figure 11. L'architecture des réseaux de neurones convolutifs.

Cette architecture des réseaux neuronaux convolutifs (CNNs) ci - dessus regorge trois couches majeurs, dont :

? Couche d'entrée : la couche d'entrée accepte généralement l'entrée tridimensionnelle sous la forme (hauteur x largeur) de l'image et a une profondeur représentant les canaux de couleur (généralement trois pour les canaux de couleur RGB).

P a g e | 34

V' Couche d'entrainement : est construite de :

? Convolution couche.

? Fonction d'activation : Linéaire rectifiée « Relu ». ? Couche de mise en commun « pooling ».

V' Couche de classification : la couche de classification permet de produire des probabilités ou des scores de classe.

2.5.1. Les filtres (Kernel).

Un filtre est un petit groupe de neurones à partir desquels la couche suivante est connectée. Comme les filtres utilisés dans les traitements d'images classiques, ces derniers se distinguent des filtres ordinaires par leurs auto-apprentissages en effet, on ne connaît pas d'avance les paramètres qui les constituent, c'est au réseau de les apprendre (Aston et al., 2020).

Un filtre est une matrice de poids n X n qui analyse une partie m X m de l'image afin d'en extraire une valeur pertinente puis répéter le processus sur toute l'image.

Figure 12. Opération convolutive sur une image. 2.5.2. Cartes de caractéristiques.

Les cartes de caractéristiques (feature map) sont les images résultantes de l'opération convolutive.

Dans la pratique, plusieurs filtres sont appliqués à l'image de départ pour produire plusieurs cartes. Chacune d'entre elles a pour rôle de détecter une particularité : contraste, lumière et autres en comparaison avec les régions du cortex visuel comme suit.

P a g e | 35

Figure 13. Représentation générale des cartes de caractéristiques.

La figure ci-après est un exemple d'une première convolution sur une image histologique d'un cancer de la peau invasif. On remarque suite à une première couche de convolution une extraction générale des caractéristiques globales : couleur, contraste, luminosité...etc.

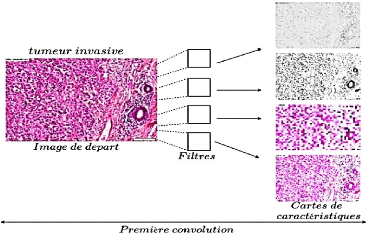
Figure 14. Convolution sur une histologie. 2.5.3. Profondeur de l'image et des filtres.

Une image est pour une machine une matrice de (n X n X k), n représente les lignes et les colonnes qui constituent ses pixels. Chaque pixel dispose de 3 valeurs du système de codage RGB : c'est la dimension k. Par conséquent, un filtre est en réalité de taille m X m X k.

P a g e | 36

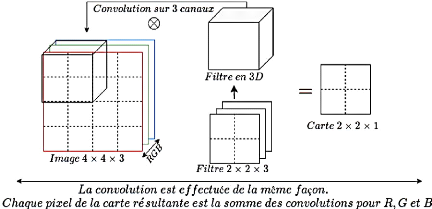
Figure 15. Dimensions d'une image et des cartes de caractéristiques.

Résultat : le nombre poids est drastiquement diminué en terme de lignes et colonnes mais augmenté en profondeur par le rajout de la 3^ème dimension k.

La dimension des images est également augmentée en profondeur à cause du nombre de cartes générées.

Un des objectifs primaires des CNN étant de réduire la dimension, celle-ci se voit augmentée (Aston et al., 2020).

2.5.4. Le Pooling.

Le Pooling (mise en commun) est un algorithme visant à réduire la dimension d'une image tout en gardant des sous-parties importantes.

La fenêtre de Pooling est une matrice m x m, qui parcours l'image afin de produire un seul pixel de sortie parmi mxm pixels voisins. Plusieurs méthodes de production de pixels sont mises en place en fonction de la pertinence de l'information voulue.

Parmi ces méthodes, on compte l'average-Pooling, max et min-Pooling (Aston et al., 2020).

2.5.4.1. Average-Pooling.

Le principe de l'average-Pooling est de prendre la moyenne des m X m pixels voisins. Dans le traitement d'image, on parle de " lissage". La fenêtre de Pooling la plus utilisée est de 2 X 2.

P a g e | 37

2.5.4.2. Max-Pooling.

Le Max-Pooling permet d'extraire uniquement la plus grande valeur dans un ensemble de pixels. Ce type de Pooling est avantageux pour analyser une image dont le fond est noir. Le but est ainsi d'ignorer tous les pixels de faible valeur (en noir) et d'en extraire l'avant-plan (plus clair).

2.5.4.3. Min-Pooling.

Le Min-Pooling permet d'extraire le pixel le plus faible parmi ses m X m pixels voisins. Cette méthode est adaptée dans les cas où le fond de l'image est clair et l'avant plan sombre.

La figure suivante illustre les différents résultats de Pooling et leurs effets réducteurs.

Figure 16. Exemple applicatif des différents Pooling.

Remarque : théoriquement, l'Average-Pooling semble être la méthode la plus adéquate car on ne perd ni trop ni peu d'informations. Cependant, les expériences ont montré que dans la plupart des problèmes de traitement d'images, le Max-Pooling semble être la plus adéquate. La figure suivante représente un test de différents Pooling sur une histologie.

P a g e | 38

Figure 17. Résultat de différents Pooling sur une histologie.

Résultat : Le Max-Pooling permet d'extraire de meilleurs contours afin de détecter les anomalies (grosseur de cellules) tandis que l'Average-Pooling ne fait que lisser l'image. Quant au Min-Pooling, il permet que de réduire la luminosité de l'image, les contours sont donc négligés.

2.5.5. Le Stride.

L'opération de convolution s'effectue en déplaçant successivement la fenêtre du filtre dans l'image. Le Stride est donc la taille du pas de déplacement en matière de ligne et colonne qu'on veut effectuer pour parcourir l'image.

Remarque : Les Strides les plus utilisées sont de (1; 1) ou (2; 2) afin d'avoir une meilleure corrélation entre pixels.

Figure 18. Stride(ligne,colone).

P a g e | 39

2.5.6. Le zero-Padding.

Le Zero-Padding est une technique qui permet d'ajouter des pixels à valeur nulle à chaque côté des frontières de l'image. Le but est de compléter celle-ci dans le cas où le Stride et la taille du filtre ne sont pas compatibles à celle de l'image.

Figure 19. Exemple de dépassement d'une image par un filtre.

Les pixels aux extrémités de l'image sont faiblement traités par rapport aux pixels au centre suite au déplacement du filtre. La figure suivante illustre ce phénomène.

Figure 20. Exemple de filtre passant par un pixel.

P a g e | 40

2.5.7. Padding-valid, Padding-Same.

Le Padding-Valid est caractérisé par l'absence de Padding. Quand la taille du filtre et de l'image adhère, il n'y a pas nécessité de rajouter des zéros. Le PaddingSame est introduit de sorte à avoir la taille de l'image en entrée égale à celle en sortie. C'est le plus utilisé car tous les pixels seront traités le même nombre de fois par le filtre (Aston et al., 2020).

Figure 21. Exemple applicatif d'un Padding-Same.

2.6. Fonction Relu.

L'opération de convolution sur une image impose de la linéarité à celle-ci, or les images sont naturellement non linéaires. Afin d'avoir une meilleure interprétation, Relu permet de casser cette linéarité⁸. Pratiquement, la fonction relu supprime tous les éléments noirs, en ne gardant que ceux qui portent une valeur positive (les couleurs grises, blanches et autres).

De plus, quand deux couches de convolution sont appliquées, les poids des filtres de la 2^ème convolution peuvent prendre soit des valeurs positives ou négatives. Si la carte de caractéristique de la 1^ère convolution est négative, le produit d'une réponse négative et d'un poids de filtre négatif produira une valeur positive. Pourtant, le produit d'une réponse positive et d'un filtre positif produira également une valeur positive. En conséquence, le système ne peut pas différencier ces deux cas (Jay Kuo, 2016).

⁸ C'est - à - dire remplacés les résultats négatifs par zéro.

P a g e | 41

Figure 22. Opération convolutive sans Relu.

La figure suivante illustre l'impact de la rectification linéaire sur les cartes de caractéristiques résultantes en effet, deux filtres de signes différents produisent deux cartes différentes.

Figure 23. Opération convolutive avec Relu. 2.7. Couche de Correction (RELU).

Après chaque opération de convolution, le réseau de neurones convolutif applique une transformation ReLU (unité de rectification linéaire) à la fonction convoluée, afin d'introduire la non-linéarité dans le modèle. La fonction ReLU, F(x) = max (0, x), renvoie x pour toutes les valeurs de x > 0 et renvoie 0 pour toutes les valeurs de x = 0.

2.8. Couche entièrement connectée (FC).

Après plusieurs couches de convolution et de max-pooling, le raisonnement de haut niveau dans le réseau neuronal se fait via des couches entièrement connectées. Les neurones dans une couche entièrement connectée ont des connexions vers toutes les sorties de la couche précédente. Leurs fonctions d'activations peuvent

P a g e | 42

donc être calculées avec une multiplication matricielle suivie d'un décalage de polarisation.

2.9. Couche de perte (LOSS).

La couche de perte spécifie comment l'entrainement du réseau pénalise l'écart entre le signal prévu et réel. Elle est normalement la dernière couche dans le réseau. Diverses fonctions de perte adaptées à différentes tâches peuvent y être utilisées. La fonction « Softmax » permet de calculer la distribution de probabilités sur les classes de sortie.

2.10. Deep Neural Network (DNN) final.

Un CNN est une succession de couches convolution/Relu appliquées aux cartes de caractéristiques résultantes. Ces opérations s'achèvent par un réseau de neurones complètement connecté afin d'assembler toutes les informations apprises et ainsi effectuer les opérations classiques d'un DNN à savoir : prédiction, estimation de l'erreur, propagation de gradients puis mise à jour des poids.

2.11. Structure générale d'un CNN.

Figure 24. Architecture générale d'un CNN. 2.12. L'application des réseaux neuronaux convolutifs.

Les réseaux neuronaux convolutifs (CNNs) ont de larges applications, notamment :

V' La reconnaissance d'image et vidéo.

V' Les systèmes de recommandation.

V' Le traitement du langage naturel.

V' L'efficacité des CNN dans la reconnaissance de l'image (Voir Figure 25) est l'une des principales raisons pour lesquelles le monde reconnaît le pouvoir de l'apprentissage profond (Patterson et al., 2017).

P a g e | 43

Figure 25. Reconnaissance d'une image avec CNN. 2.13. Avantages de CNNs.

L'utilisation d'un poids unique associé aux signaux entrant dans tous les neurones d'un même noyau de convolution est un avantage majeur des réseaux convolutifs. Par cette méthode, il y'a réduction de l'empreinte mémoire, amélioration des performances et permet une invariance du traitement par translation. C'est le principal avantage du CNN par rapport au MLP, qui lui considère chaque neurone indépendant et donc affecte un poids différent à chaque signal entrant. Lorsque le volume d'entrée varie dans le temps (vidéo ou son), il devient intéressant de rajouter un paramètre de temporisation (delay) dans le paramétrage des neurones. On parlera dans ce cas de réseau neuronal à retard temporel (TDNN).

Comparés à d'autres algorithmes de classification de l'image, les réseaux de neurones convolutifs utilisent relativement peu de prétraitement. Cela signifie que le réseau est responsable de faire évoluer tout seul ses propres filtres (apprentissage sans supervision), ce qui n'est pas le cas d'autres algorithmes plus traditionnels. L'absence de paramétrage initial et d'intervention humaine est un atout majeur des CNN.

P a g e | 44