étude du comportement de la flèche d’un matériau composite en vibration et simulation sous Matlab.

Année académique : 2015-2016

REPUBLIQUE DU CAMEROUN REPUBLIC OF CAMEROON

***************** ******************

Paix-Travail-Patrie Peace-Work-Fatherland

********** **************

MINISTERE DE L'ENSEIGNEMENT SUPERIEUR MINISTRY OF HIGHER EDUCATION

************************ ********************

UNIVERSITE DE DOUALA

ECOLE DOCTORALE DES SCIENCES FONDAMENTALES ET
APPLIQUEES (ED-SFA)

UNITE DE FORMATION DOCTORALE DES SCIENCES DE L'INGENIEUR (UFD-SI)
LABORATOIRE DE MECANIQUE ET PRODUCTIQUE (LMP)

AXE 1 : CAO & STRUCTURES

MEMOIRE DE MASTER II/DEA
Présenté par :

BETENE OMGBA Achille Désiré (15S5477)

DIPET II en Construction Mécanique
Sur le thème :

Présenté le 23 Mai 2017, à l'ENSET de Douala, salle SD1, devant le jury :

Prof. NJEUGNA E. Professeur à l'Université de Douala (ENSET) Président

Prof. ATANGANA A. Maître de Conférence à l'Université de Douala (ENSET) Directeur de mémoire

Dr. DJUINA André Chargé de Cours à l'Université de Douala (ENSET) Examinateur

Dr. BETENE EBANDA Chargé de Cours à l'Université de Douala (ENSET) Examinateur

DEDICACE

A mon fils,

II

James Léon Marvel NTSAMA BETENE

iii

REMERCIEMENTS

Les travaux de recherche présentés dans ce mémoire de Master II/DEA ont été menés de Juillet 2016 à Décembre 2016, à l'Université de Douala au sein de l'Unité de Formation Doctorale des Sciences de l'Ingénieur, de l'Ecole Doctorale des Sciences fondamentales et appliquées, Laboratoire de Mécanique et Productique.

Je tiens à remercier tout d'abord mon Directeur de mémoire, Professeur Jean A. ATANGANA de m'avoir attribué ce thème de mémoire qui m'a fait découvrir le domaine passionnant du comportement des flèches en vibration. Je voudrais lui témoigner ma profonde gratitude pour sa disponibilité, sa rigueur Scientifique et pour l'ambiance conviviale de travail qui a régné au cours du déroulement de ce mémoire, sans oublié l'admirable travail qu'il abat pour le suivi du planning de ce programme d'étude au sein de son auguste Laboratoire. Il m'a beaucoup apporté dans l'aboutissement de ce travail par ses encouragements, ses éclaircissements ainsi que nos précieux échanges tant d'un point de vue numérique que théorique.

J'adresse également mes sincères remerciements au Pr. NJEUGNA Ebenezer et au Dr. DJUINA André pour avoir accepté d'examiner mes travaux de mémoire. Qu'il me soit permis de leur exprimer ici ma profonde gratitude.

J'adresse mes remerciements au Dr BETENE Fabien pour son aide et ses conseils en matière d'expertise sur les matériaux composites et pour la motivation sans faille qu'il a assigné en moi pour l'accomplissement de ce travail, ce fut un grand plaisir de collaborer ensemble.

J'adresse mes remerciements au Dr. NOAH Pierre pour ses multiples conseils tant sur le plan des matériaux composites que sur le plan de la recherche des Sciences de l'Ingénieur.

Je remercie Monsieur le Coordonnateur de l'Ecole Doctorale des Sciences Fondamentales, le Professeur MOUKENGUE pour sa brillante coordination et à sa bienveillance sur la tenue du planning des activités de Master II recherche/DEA.

Je remercie tous les enseignants de l'Unité de Formation Doctorale, pour leur disponibilité à la dispense des unités de valeurs.

Mes chaleureux remerciements vont à toute ma famille pour son soutien moral indéfectible, en particulier M. OMGBA Pierre, Mme NGONO BETENE, M. NTSAMA Serge et Mlle. ABOMO Chantale.

Je remercie personnellement ASSOMO Pélagie, pour sa patience, sa motivation et sa compréhension dans l'accomplissement de ce travail.

Je remercie mes camarades de promotion et toute personne de près ou de loin ayant contribué à l'accomplissement de ce travail.

RESUME

Les performances séduisantes des composites entraînent de jour en jour leur intégration dans la réalisation et l'optimisation des ouvrages industriels, aéronautique, automobile, architecture, génie civil et sport. Une fois intégré dans une structure sous forme de poutre, plaque ou coque, ces composites subissent des comportements dynamiques en particulier des vibrations transversales de flexion. Pour le concepteur, ce comportement doit être prédit et garanti au cours de la conception, par une bonne modélisation des déplacements des points de la structure. Aussi, au LMP, au LAMMA et au Génie Mécanique de l'ENSET de Douala, les composites se font développés, mais une véritable modélisation comportementale n'est pas encore effectuée en particulier l'aspect vibratoire. Ce sont les raisons pour lesquelles, nous avons mené ces travaux portant sur « l'étude du comportement de la flèche d'un matériau composite en vibration mécanique et simulation sous Matlab ».

Face à la pluridisciplinarité des sollicitations, nous avons restreint l'étude à des structures composites de types plis unidirectionnel à 0° ou 90° et stratifié croisé symétrique ou antisymétrique [0/90]S vibrantes et sollicitées en flexion pure. L'objectif principal poursuivi au cours de cette recherche est de prédire le comportement de la flèche d'une structure orthotrope renforcée par des fibres végétales locales. Pour y parvenir, des études analytique et numérique ont été menées. La résolution analytique faite au moyen des méthodes de séparation des variables, puis de Rayleigh-Ritz de l'équation de mouvement transverse exprimée par la Théorie Classique des Stratifiés (TCS) formulée sur le modèle des plaques de Love-Kirchhoff puis, étendue sur le modèle des poutres de Euler-Bernoulli nous a permis d'obtenir les équations de comportement de la flèche de différentes structures avec diverses conditions aux limites. La modélisation numérique a d'abord fait l'objet, de simulation sous Matlab en introduisant les équations de la flèche formulées analytiquement, les paramètres d'un composite à matrice polyester, renforcé par des fibres de Rhecktophyllum camerunense (RC), ensuite, sur la simulation numérique par éléments finis sous Abaqus du même composite et enfin sur la mise sur pieds du logiciel Inflexion - Vibration Arrow Composite (i-VAC) qui permet de prédire le comportement de la flèche des composites étudiés dans le cadre de ce travail.

Les résultats de la simulation numérique sous Matlab s'accordent avec un écart relatif moyen de 0,026625% aux résultats de la simulation sous Abaqus et avec un écart relatif moyen de 0,6% aux résultats d'une étude expérimentale tirée de la littérature. Par ailleurs, il a été établi que, pour réduire la flèche d'une structure, il faut choisir des éléments de longueur réduite, de hauteur supérieure ou égale à 15 mm (poutres), avec un taux de fibres supérieur ou égal à 35% de module d'Young longitudinal moyen supérieur ou égal à 8,5 GPa.

iv

Mots clés : Matériaux composite ; Flèche ; Vibration mécanique ; Flexion ; Matlab ; Abaqus ; i-VAC.

ABSTRACT

The tempting performances of the composites involve day by day, their integration in the realization and the optimization of the industrial works, aeronautics, car, architecture, civil engineer and sport. Once integrated in a structure in the form of beam, plate or hull, these composites undergo dynamic behaviors in particular transverse vibrations of inflection. For the originator, this behavior must be predicted and guaranteed during the design, by a good modeling of displacements of the points of the structure. Also, with the LMP, the LAMMA and the Mechanical engineer of the ENSET of Douala, the composites are done developed, but a true behavior in modeling is not carried out yet in particular the vibratory aspect. It is the reasons for which, we undertook these works relating to « the study of the behavior of the arrow of a composite material in mechanical vibration and simulation under Matlab ».

In front of the multidisciplinary requests, we restricted the study with composite structures of standard folds one-way with 0° or 90° and laminated symmetrical crusader [0/90]s or antisymmetric vibrating and requested in pure inflection. The main aim pursued during this research is to predict the behavior of the arrow of an orthotropic structure reinforced by vegetable local fiber. For that purpose, of the studies analytical and digital were carried out. The analytical resolution made by means of the methods of separations of the variables, then of Rayleigh-Ritz of the transverse equation of motion expressed by the TCS formulated on the model of the plates of Coils-Kirchhoff then, wide on the model of the beams of Euler-Bernoulli enabled us to obtain the equations of behavior of the arrow of various structures with various boundary conditions. Digital modeling was initially the subject, with simulation under Matlab while introducing with the equations of the arrow formulated analytically, the parameters of a composite with matrix polyester, reinforced by fiber of Rhecktophyllum camerunense (RC), then, on the digital simulation by finite elements under Abaqus of the same composite and finally on the setting-up of the software i-VAC which makes it possible to predict the behavior of the arrow of the composites studied within the framework of this work.

The results of the digital simulation under Matlab agree with an average variation relative of 0.026625% to the results of simulation under Abaqus and with an average variation relative of 0.6% to the results of an experimental study drawn from the literature. In addition, it was established that, to reduce the arrow of a structure, it is necessary to choose elements reduce length, higher or equal to height 15 mm (beams), with a rate of fibers equal to or higher than 35% of average longitudinal modulus Young equal to or higher than 8.5 GPa.

V

Keys Words : Composites materials ; Arrow ; Mechanical vibration ; Inflexion.

vi

TABLE DES MATIERES

DEDICACE . ii

REMERCIEMENTS iii

RESUME . iv

ABSTRACT . v

TABLE DES MATIERES vi

LISTE DES FIGURES x

LISTES DES TABLEAUX xii

LISTES DES SYMBOLES ET ABREVIATIONS xiii

INTRODUCTION GENERALE 1

CHAPITRE 1 : ETAT DE L'ART SUR LE COMPORTEMENT VIBRATOIRE D'UN

MATERIAU COMPOSITE. 3

1.1. Présentation générale des matériaux composites 4

1.1.1. Définition générale des composites 4

1.1.2. Classification générale des fibres développés au LMP 4

1.1.3. Choix des structures composites utilisées 4

1.2. Théorie classique des stratifiés 5

1.2.1. Hypothèses de la théorie des stratifiés 5

1.2.2. Comportement mécanique d'une structure stratifié. 5

1.3. Formulation de la théorie classique des stratifiées 6

1.3.1. Hypothèses de Love-Kirchhoff 6

1.3.2. Expression du champ de déplacement cinématiquement admissible 6

1.3.3. Expression générale du champ de déformation 7

1.3.4. Expression du champ de contraintes 8

1.3.5. Expression des résultantes en membrane et des moments 9

1.3.6. Equation constitutive générale d'un stratifié en l'absence du cisaillement 10

1.4. Comportement statique des matériaux composites orthotropes 11

1.4.1. Les différents paramètres de la flexion pure d'une plaque orthotrope 12

1.4.2. Les différents paramètres de la flexion cylindrique d'une structure orthotrope 13

1.5. Comportement vibratoire des matériaux composites 14

1.5.1. Notion de la flèche 14

1.5.2. Les types de flèches 14

1.5.2.1. Analyse à partir des vibrations d'une poutre 14

1.5.2.2. Analyse à partir des vibrations des plaques et coques 15

1.6. Méthodes de résolution et théories des problèmes de vibration 16

1.7. Cadre de validité de la recherche 16

1.7.1. Problématique de la recherche 16

1.7.2. Couplage vibratoire 17

1.7.3. Code de calcul développé 18

1.7.4. Objectif de la recherche 18

1.7.5. La méthode mathématique utilisée dans le cadre de la recherche 18

CHAPITRE 2 : FORMULATION THEORIQUE DE L'EQUATION DE COMPORTEMENT DE LA FLECHE EN VIBRATION DE FLEXION D'UNE STRUCTURE

ORTHOTROPE 20

2.1. Définition des paramètres du problème. 21

2.1.1. Champ de déplacement cinématiquement admissible du problème 21

2.1.2. Champ de déformation 21

2.1.3. Champ de déformation 21

2.1.4. Equation constitutive et condition d'équilibre dynamique de la structure 21

2.1.5. Les différents problèmes de flexion à traiter 22

2.2. Vibrations en flexion pure des poutres orthotropes 22

2.2.1. Cas d'une poutre orthotrope en appuis simples (AA) 23

2.2.2. Cas d'une poutre orthotrope encastrées sur ses deux extrémités (EE) 25

2.2.3. Cas d'une poutre orthotrope encastrée et libre (EL) 27

2.3. Expressions explicites de la flèche d'une plaque stratifiée orthotrope 29

2.3.1. Cas d'une plaque orthotrope en appuis simples (AAAA) 29

2.3.2. Approche par la méthode de Rayleigh 32

2.3.3. Energie de déformation 32

2.3.3.1. Energie cinétique 32

2.3.3.2. Formulation du théorème d'énergie en théorie des stratifiées 32

2.3.4. Cas d'une plaque orthotrope à côtés encastrés (EEEE) 33
2.3.1. Cas d'une plaque orthotrope à deux côtés opposés encastrés et les deux autres en appuis

simples (AEAE) 33

CHAPITRE 3 : SIMULATION NUMERIQUE SOUS MATLAB DU COMPORTEMENT DE LA

FLECHE D'UNE STRUCTURE COMPOSITE. 35

3.1. Notion de simulation sous Matlab 36

3.1.1. Objectif de la simulation sous Matlab 36

3.1.2. Intérêt de la simulation sous Matlab 36

3.2. Présentation du composite étudié 36

3.3. Programmation des équations de la flèche sous Matlab 36

3.3.1. Présentation des éléments et des conditions aux limites de la simulation 37

3.3.2. Modélisation des éléments dans le cas de l'élément poutre 37

3.3.2.1. Cas d'une poutre EE 37

3.3.2.2. Cas d'une poutre EL 46

3.3.2.3. Cas d'une poutre AA 48

3.3.2.4. Conclusion simulation des poutres 50

3.3.3. Modélisation des éléments dans le cas d'une plaque en appuis simples 50

CHAPITRE 4 : SIMULATION NUMERIQUE SOUS ABAQUS DU COMPORTEMENT DE LA FLECHE D'UNE STRUCTURE COMPOSITE ET VALIDATION DU CODE DE

CALCUL 54

4.1. Présentation de la méthode des éléments finis 55

viii

4.1.1. Principe de la méthode des éléments finis 55

4.1.2. Différentes étapes de la méthode des éléments finis 55

4.2. Modélisation du comportement de la flèche d'un matériau composite en vibrations libres

transverses 55

4.2.1. Intérêt de la modélisation numérique 55

4.2.2. Justification du choix de ABAQUS 56

4.2.3. Présentation du composites étudiés 57

4.2.3.1. Objectif de la modélisation 57

4.2.3.2. Constituants des composites étudié 57

4.2.3.3. Eléments à modéliser 57

4.2.3.4. Les conditions aux limites à étudier 57

4.3. Modélisation par éléments finis avec ABAQUS du comportement de la flèche d'un matériau

composite en vibrations libres transverses 57

4.3.1. Présentation du logiciel ABAQUS 57

4.3.2. Comportement de la flèche des plaques par la méthode des éléments finis et comparaison avec les

résultats du code développé. 59

4.3.2.1. Conditions aux limites : plaque en appuis simples sur ses quatre côtés 59

4.3.2.2. Conditions aux limites : poutre encastrée à une extrémité et libre sur l'autre. 62

4.4. Validation du code de calcul 64

4.4.1. Présentation des travaux de M. Assarar, A. El Mahi & J.-M. Berthelot [13] 64

4.4.2. Mise en situation des travaux 64

4.4.2.1. Présentation du composite et description de l'étude 64

4.4.2.2. Résultats de l'étude 65

4.4.3. Calcul des fréquences avec le code de calcul 65

4.4.4. Comparaison des deux résultats 66

CHAPITRE 5 : MISE EN PLACE D'UN LOGICIEL DE CALCUL DE LA FLECHE D'UN

COMPOSITE ORTHOTROPE ET CAS PRATIQUE 68

5.1. Mise en place d'un logiciel de calcul de la flèche d'un composite 69

5.1.1. Objectif de la conception du logiciel 69

5.1.2. Choix de l'outils de développement 69

5.1.3. Présentation des attributs du logiciel 69

5.1.3.1. Nom du logiciel 69

5.1.3.2. Architecture du logiciel 69

5.1.3.3. ` Fonction principale du logiciel 70

5.1.4. Petit tutoriel de i-VAC 71

5.2. Cas pratique : optimisation du support d'un panneau de signalisation 73

5.2.1. Mise en situation 73

5.2.2. Problématique de l'optimisation 73

5.2.3. Objectif de l'optimisation 74

5.2.4. Etude vibratoire du système 74

5.2.4.1. Hypothèses de l'étude et données 74

5.2.4.2. Bilan des actions mécaniques exercées sur le système 74

5.2.4.3. Champ de déplacement cinématiquement admissible du système 75

5.2.4.4. Expression du moment fléchissant 75

5.2.4.5. Flèche maximale du système 75

5.2.4.6. Présentation et comparaison avec la flèche maximale 76

ix

CONCLUSION GENERALE : BILAN ET PERSPECTIVES 77

ANNEXES 78

Annexes 1 : Coefficients intervenants dans le calcul des fréquences propres 78

Annexes 2 : Caractéristiques des fibres intégrées dans le logiciel i-VAC 78

Annexes 3 : Les caractéristiques des matrices intégrées dans le logiciel i-VAC 79

Annexes 4 : Classe des moments de flexion normalisées 79

BIBLIOGRAPHIE 86

X

LISTE DES FIGURES

Titres pages

Figure 1.1 : (a) Diagramme de définition d'un composite ; (b) Différentes constituant d'un composite. 4

Figure 1.2 : Classification des fibres végétales développées au LMP [1]. 4

Figure 1.3 : Schématisation d'une plaque selon Love-Kirchhoff [2] 6

Figure 1.4 : Bilan des actions mécaniques appliquées à un élément de la plaque 9

Figure 1.5 : Schéma d'un stratifié à n couches 10

Figure 1.6 : Cchémas d'une plaque pour flexion cylindrique. 12

Figure 1.7 : Schémas d'une plaque pour flexion cylindrique. 13

Figure 1.8 : Images de quelques structures soumises aux vibrations [8-9-10] 17

Figure 2.9 : Schéma d'une poutre en appuis simples sur ses deux extrémités 23

Figure 2.10 : Schéma d'une poutre encastrée sur ses deux extrémités 25

Figure 2.11 : Schéma d'une poutre en appuis simples sur ses deux extrémités 27

Figure 2.12 : Plaque rectangulaire en appuis simples sur ses 4 côtés (AAAA) 29

Figure 2.13 : Plaque rectangulaire encastrée sur ses 4 côtés (EEEE) 33

Figure 2.14 : Plaque encastrée sur 2 côtés consécutifs et en appui simple sur les 2 autres (AEAE). 33

Figure 3.15 : Graphe de variation de la flèche maximale pour les 6 premiers modes 37

Figure 3.16 : Graphe de variation de la flèche maximale en fonction des modes 38

Figure 3.17 : Influence de la longueur de la poutre sur le comportement de la flèche 39

Figure 3.18 : Comportement de la flèche sur une poutre EE de longueur 500 mm 39

Figure 3.19 : Influence de la longueur de la poutre EE sur les fréquences angulaires propres 40

Figure 3.20 : Influence de la hauteur de la poutre (EE) sur le comportement de la flèche. 40

Figure 3.21 : Influence de la hauteur de la poutre (EE) sur les caractéristiques vibratoires. 41

Figure 3.22 : Influence de la hauteur de la poutre (EE) sur les fréquences angulaires 41

Figure 3.23 : Influence du type de section d'une poutre (EE) sur les fréquences angulaires. 43

Figure 3.24 : Influence du taux de fibres sur le comportement de la flèche d'une poutre (EE) 43

Figure 3.25 : Influence du taux de fibres sur les fréquences angulaires dans une poutre (EE) 44

Figure 3.26 : Influence du module d'Young des fibres sur le comportement de la flèche de la poutre (EE). 45

Figure 3.27 : Influence du taux de fibres sur les fréquences angulaires dans une poutre (EE) 45

Figure 3.28 : Comportement de la flèche pour les 6 premiers modes d'une poutre EL 46

Figure 3.29 : Graphe de variation de la flèche maximale en fonction des modes 46

Figure 3.30 : Influence du taux de fibres sur le comportement de la flèche d'une poutre (EL). 47

Figure 3.31 : Influence un taux de fibres > 35% de la poutre (EL) sur les caractéristiques vibratoires. 48

Figure 3.32 : Influence un taux de fibres < 35% de la poutre (EL) sur les caractéristiques vibratoires. 48

Figure 3.33 : Comportement de la flèche pour les 8 premiers modes d'une poutre AA 48

xi

Figure 3.34 : Comportement de la flèche en fonction de la longueur d'une poutre AA 49

Figure 3.35 : Comportement de la flèche en fonction de la hauteur d'une poutre AA 49

Figure 3.36 : Comportement de la flèche en fonction du taux de fibre dans la poutre AA 50

Figure 3.37 : Comportement de la flèche d'une plaque AAAA (pli à 0°) pour 5 modes. 51

Figure 3.38 : Comportement de la flèche d'une plaque AAAA (pli à 0°) pour 5 modes. 52

Figure 3.39 : Comportement de la flèche d'une plaque AAAA (pli à 90°) pour 5 modes. 52

Figure 3.40 : Comportement de la flèche d'une plaque AAAA (SS à [0/90]_s) pour 5 modes. 53

Figure 3.41 : Comportement de la flèche d'une plaque AAAA (stratifié antisymétrique à [0/90]_s). 53

Figure 4.42: Présentation graphique du comportement de la flèche sur un pli orthotrope 59

Figure 4.43 : Ecart relatif entre la flèche maximale calculée par MATLAB et celle calculée par ABAQUS 60

Figure 4.44 : Influence du nombre d'éléments sur le comportement de la flèche d'une plaque en appuis simples. 61

Figure 4.45 : Comportement de la flèche sur une plaque en appuis simples sur ses 4 extrémités. 62

Figure 4.46 : Présentation graphique du comportement de la flèche sur une poutre EL 62

Figure 4.47 : Comportement de la flèche sur un pli orthotrope en appuis simples sur ses 4 extrémités. 63

Figure 4.48 : Présentation graphique du comportement de la flèche sur une poutre EL 64

Figure 4.49 : Stratifié croisé symétrique considéré pour l'étude 65

Figure 4.50: Dispositif expérimental utilisé [13]. 65

Figure 4.51: Dispositif expérimental utilisé. 66

Figure 4.52 : Différentes étapes à suivre pour analyser le comportement de la flèche 70

Figure 4.53 : Aperçu de l'écran de démarrage et d'accueil du logiciel i-VAC. 71

Figure 4.54 : Aperçu de l'interface de l'ongle MATERIAU du logiciel i-VAC 71

Figure 4.55 : Aperçu de de l'interface de l'ongle HOMOGENEISATION du logiciel i-VAC 72

Figure 4.56 : Aperçu de de l'interface de l'ongle CARACTERISTIQUES du logiciel i-VAC 72

Figure 4.57 : Aperçu de de l'interface de l'ongle RESULTATS du logiciel i-VAC. 72

Figure 4.58 : Images de différents panneaux de signalisation. [23] 73

Figure 5.59 : Schéma annoté d'un panneau de signalisation routière 73

Figure 5.60 : Schéma annoté d'un panneau de signalisation routière 75

xii

LISTES DES TABLEAUX

Titres pages

Tableau 3.1 : Tableau des caractéristiques des constituants 36

Tableau 3.2 : Présentation des différentes conditions aux limites 37

Tableau 3.3 : Valeurs des flèches maximales pour les 10 premiers modes d'une poutre EE 38

Tableau 3.4 : Flèches maximales avec différentes longueurs pour 5 modes d'une poutre EE. 38

Tableau 3.5 : Fréquences angulaires maximales avec différentes longueurs pour 5 modes d'une poutre EE. . 39

Tableau 3.6 : Flèches maximales pour différentes hauteurs des 5 premiers modes d'une poutre EE. 40

Tableau 3.7 : Fréquences maximales pour différentes hauteurs des 5 premiers modes d'une poutre EE 41

Tableau 3.8 : Flèches maximales pour différentes sections d'une poutre EE pour les 5 premiers modes. 42

Tableau 3.9 : Fréquences maximales pour différentes section d'une poutre EE pour les 5 premiers modes. 42

Tableau 3.10 : Flèches maximales pour différents taux de fibres d'une poutre EE pour les 5 premiers modes 43

Tableau 3.11 : Fréquences maximales pour différents taux de fibres d'une poutre EE pour les 5 premiers modes. 44

Tableau 3.12 : Flèches maximales pour différents Ef d'une poutre EE pour les 5 premiers modes 44

Tableau 3.13 : Fréquences maximales pour différents Ef d'une poutre EE pour les 5 premiers modes. 45

Tableau 3.14 : Valeurs des flèches maximales pour les 10 premiers modes d'une poutre EL 46

Tableau 3.15 : Flèches maximales pour différents taux de fibres d'une poutre EL pour les 5 premiers modes 47

Tableau 3.16 : Flèches maximales avec différentes longueurs pour les 5 premiers modes d'une poutre AA. 49

Tableau 3.17: Flèches maximales avec différentes longueurs pour les 5 premiers modes d'une poutre AA. 49

Tableau 3.18: Flèches maximales avec différentes longueurs pour les 5 premiers modes d'une poutre EE. 50

Tableau 3.19 : Valeurs des flèches maximales pour les 5 premiers modes d'une plaque AAAA 51

Tableau 4.20 : Présentation géométrique des éléments à modéliser 57

Tableau 4.21 : Comparaison des résultats obtenus par ABAQUS avec ceux du code développé. 59

Tableau 4.22 : Comportement de la flèche d'une plaque AAAA en fonction du nombre d'éléments. 60

Tableau 4.23 : Comparaison des résultats obtenus par ABAQUS avec ceux du code développé. 63

Tableau 4.24: Fréquences calculées par les travaux expérimentaux de M. Assarar. 65

Tableau 4.25: Résultats des fréquences calculées par le code développé 66

Tableau 4.26 : Comparaison des fréquences calculées par Matlab avec celles obtenues par M. Assarar. 66

Tableau A1.27: Coefficients intervenants dans le calcul des fréquences propres d'un composite orthotrope (E :

côté encastré ; S : côté en appui simple). [3] 78

Tableau A2.28 : caractéristiques mécaniques et masse volumique de quelques fibres [13] 78

Tableau A2.29 : Caractéristiques mécaniques de quelques fibres végétales extraites au Département Génie

Mécanique de l'ENSET de Douala. 78

Tableau A3.30 : Caractéristiques des matrices. 79

Tableau A4.31 : caractéristiques géométriques des supports types : SP (a) ; SD1 (b) et SD2 (c) [23] 79

Tableau A4.32 : caractéristiques géométriques des supports type SD3 79

Tableau A6.33 : les différentes classes des moments de flexion normalisées [23] 80

xiii

LISTES DES SYMBOLES ET ABREVIATIONS

Liste des symboles

Symboles	Désignations	Unités
	Dimension de la structure suivant x	[mm]
	Dimension de la structure suivant y	[mm]
	Hauteur ou épaisseur de la structure suivant z	[mm]
	Coefficients de la matrice de rigidité	[MPa]
	Coefficient de la matrice de rigidité réduite	[MPa]
	Coefficient de la matrice de rigidité membranaire	[N/mm]
	Coefficient de la matrice de rigidité en couplage membrane-flexion- torsion	[N]
	Coefficient de la matrice de rigidité en flexion	[N.mm]
	Module d'Young ( , L : Longitudinal ; T : Transversal)	[MPa]
	Coefficient de Poisson
	Module de cisaillement transverse	[MPa]
	Tenseur de déformation
	Tenseur de déformation membranaire
	Tenseur de déformation en flexion
	Tenseur des courbures
	Tenseur des efforts membranaires	[N]
	Tenseur des moments de flexion et torsion	[N/mm]
	Tenseur des contraintes	[MPa]
	Force par unité de volume	[N/mm^3]
	Force par unité de surface	[N/mm^2]
; ;	Coefficient des fonctions de déplacement
	Fréquence angulaire des vibrations	[rad/s]
	Déformée modale
;	Mode d'excitation suivant x et y
	Energie cinétique	[J]
	Energie de déformation	[J]
	Ecart relatif

Liste des abréviations

TCS : Théorie Classique des Stratifiés ;

CAO : Conception Assistée par Ordinateur ;

ENSET : Ecole Normale Supérieure d'Enseignement Technique ;

MATLAB : Matrix LABoratory ;

LAMMA : Laboratoire de Mécanique et des Matériaux Appliqués ;

LMP : Laboratoire de Mécanique et Productique.

1

INTRODUCTION GENERALE

Depuis des années, le développement des nouvelles technologies met un accent particulier sur l'emploi des matériaux présentant un caractère biodégradable, de faible masse avec des caractéristiques mécaniques et thermiques répondants aux besoins de l'application. Toutefois, des études d'analyses des comportements en particulier l'aspect vibratoire doivent être faites par le concepteur afin de préserver les structures et les édicter contre la fatigue et la rupture. L'une des causes de rupture est la fatigue structurale due aux ondes vibratoires et l'ampleur de la flèche en vibration suite à une excitation.

L'étude ou l'analyse des vibrations n'est pas une science récente et pourtant elle connait depuis quelques années un regain d'intérêt pour des besoins de conception et de dimensionnement des structures répondant aux meilleures conditions de fonctionnement, de sécurité, d'économie, d'esthétique et d'isolation acoustique. Face à ces exigences, les matériaux composites obtenus par association de deux phases distinctes, sont une solution idéale grâce à leur multifonctionnalité intégrée. Ils se font exploités largement dans de nombreux secteurs industriels tels que l'aéronautique, l'aérospatial, la construction navale, la construction automobile, l'électroménager, le génie civil, l'acoustique, le textile et bien d'autres. Dans le domaine textile par exemple : des fibres de toutes natures consistent à former des fils par assemblage pour la confection des vêtements de protection contre le froid : à savoir les fibres d'origine animale (laine de mouton, de lapin, ...) ou végétale (lin, coton), les polymères biodégradables synthétiques obtenus à partir de l'amidon de maïs, sans oublier les céramiques et les carbones. Pour obtenir des textiles synthétiques, aussi bien pour les vêtements que pour les tissus de décoration ou d'usage intérieur (rideaux, matelas, serviettes, tapisseries...).

Aujourd'hui, le développement des matériaux composites constitue un axe de recherche particulier au sein du laboratoire de Mécanique et productique de l'Université de Douala. Seulement, l'intégration dans les lois de comportement constituent encore une épine pour les chercheurs du laboratoire. L'ensemble des études menées dans d'autres laboratoires ont prouvées que les matériaux composites réagissent mieux que les matériaux homogènes au comportement vibratoire d'autant plus que, ces études ne mettent pas en exergue le comportement de la flèche, d'où la question, comment se comporte la flèche d'un matériau composite soumis à des vibrations transversales ? La réponse à cette question, constitue l'axe principal de cette recherche portant sur la thématique intitulée : « Etude du comportement de la flèche d'un matériau composite en vibration et simulation sous Matlab ». Cette recherche, vient renforcer la volonté de cerner, de maîtriser la conception et l'optimisation des structures en matériaux composites renforcés par des fibres développées au sein du LMP, LAMMA et Génie Mécanique de l'ENSET de l'Université de Douala afin que ceux-ci s'intègrent et répondent mieux aux exigences de conception.

Ce mémoire, qui constitue le résumé des travaux de recherches menés, s'articulent sur cinq chapitres.

2

Le chapitre 1, fait état de l'art sur le comportement vibratoire d'un matériau composite. Nous présentons de façon générale les matériaux composites à travers leur définition et classification générale des fibres développées au L2M&P. Nous rappelons la théorie classique des stratifiés sur le modèle de Love-Kirchhoff, puis simplifiée par l'hypothèse de Euler-Bernoulli. Nous présentons aussi les différents paramètres de la flèche. Une analyse bibliographique dans les études de vibrations transversales est faite pour relever les travaux manquants, puis un bilan de ce chapitre est effectué pour définir le cadre de validité de notre étude.

Au chapitre 2, nous formulons l'équation de mouvement à partir de la Théorie Classique des Stratifiés en vibration transverse pour la flexion d'une plaque de Love-Kirchhoff puis transposée sur les poutres de Euler-Bernoulli. L'équation différentielle obtenue est résolue par la combinaison de la méthode de séparation des variables et la méthode de Rayleigh-Ritz. Cette résolution conduit à l'équation de comportement de la flèche d'un matériau composite orthotrope sollicité en flexion pure.

Au chapitre 3, nous effectuons une simulation numérique sous Matlab du comportement d'une poutre unidirectionnelle, puis d'une plaque unidirectionnelle et d'une plaque orthotrope à matrice polyester, renforcé par des fibres de RC pour définir les caractéristiques minimales d'une poutre sollicitée en flexion pure, soumise à des vibrations transverses afin de minimiser sa flèche.

Au chapitre 4, nous effectuons d'abord une simulation sous Abaqus du comportement de la flèche d'une plaque, puis d'une poutre en composite polyester/RC ensuite, ces résultats sont confrontés à ceux générés par le code de calcul développé au chapitre 3 et enfin, la véracité des résultats du code de calcul est établie en confrontant ceux-ci aux résultats obtenus au cours d'une expérimentation tirée de la littérature.

Au chapitre 5, nous mettons sur pieds une micro-application sous Matlab destinée à la communauté des chercheurs scientifiques et aux bureaux d'études afin de raccourcir les études de vibration en flexion des structures en plis unidirectionnels ou orthotropes, en stratifié croisé symétrique et antisymétrique. La poutre du panneau de signalisation est étudiée comme application visant à montrer que le matériau homogène peut être substitué par un composite.

3

CHAPITRE 1 : ETAT DE L'ART SUR LE COMPORTEMENT VIBRATOIRE D'UN MATERIAU COMPOSITE.

Chapitre 1 :

ETAT DE L'ART SUR LE COMPORTEMENT VIBRATOIRE
D'UN MATERIAU COMPOSITE.

Depuis les années 1980, l'utilisation des matériaux composites dans le secteur de l'automobile, aéronautique, navale, génie civil et architecture s'est fortement accélérée. Les avantages de légèreté, ténacité, dureté, longue durée de vie, haute résistance mécanique, thermique, chimique et électrique ; etc. sont des valeurs que les composites offrent et poussent les concepteurs à élaborer et à optimiser les performances des structures réalisées avec des matériaux classiques (acier, aluminium, cuivre, etc.). De plus, les composites offrent une flexibilité de formes et permettent d'aboutir à des conceptions particulières et spécifiques. Seulement, une fois intégrés dans une structure comme poutre, plaque ou coque, les composites sont souvent confrontés aux problèmes de vibrations. Dans ce chapitre, il est question de présenter d'abord la notion de composite, ensuite rappeler la théorie classique des stratifiés en statique, puis dégager les différents paramètres de la flèche en vibration et enfin définir le cadre de validité de cette recherche.

1.1. Présentation générale des matériaux composites

1.1.1. Définition générale des composites

Un matériau composite ou composite, est généralement l'union d'au moins deux phases (matrice/renfort) non miscibles, de nature différente, se complétant, dont l'ensemble des performances est supérieur à celui d'un constituant (figure 1.1). Les composites sont très hétérogènes et très anisotrope¹ de plus, ils disposent d'atouts majeurs défiant les matériaux homogènes comme : légèreté, résistance mécanique, chimique, thermique et électrique.

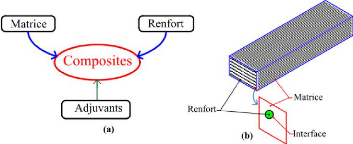
Figure 1.1 : (a) Diagramme de définition d'un composite ; (b) Différentes constituant d'un

composite.

1.1.2. Classification générale des fibres développés au LMP

Il existe une foultitude de composites, qui se distinguent et se caractérisent par leurs constituants. Les composites développés au LMP se trouvent dans la classe des composites à fibres végétales. Ces fibres végétales peuvent être classées suivant leur origine comme le montre la figure 1.2. [1J

Figure 1.2 : Classification des fibres végétales développées au LMP [1].

1.1.3. Choix des structures composites utilisées

Le diamètre des fibres d'un composite étant microscopique, les pièces composites sont généralement réalisées à partir d'éléments structurels²« prêt à mettre en forme » contenant un grand nombre de fibres, comme des fils à tisser ou des nappes. Parmi ces structures seules les plis et les stratifiés feront l'objet de notre étude car la fabrication de stratifiés offre la possibilité d'adapter le comportement du matériau aux conditions de chargement attendues.

¹ Anisotrope : variation des propriétés mécaniques suivant la direction.

² Les éléments structurels ici sont les plis, les stratifiés et les sandwiches.

Chapitre 1 : Etat de l'art sur le comportement vibratoire d'un matériau composite

1.2. Théorie classique des stratifiés

La théorie classique des stratifiées permet d'estimer, à partir des chargements macroscopiques appliqués, les champs de contraintes et de déformations à l'échelle du pli.

1.2.1. Hypothèses de la théorie des stratifiés

A l'échelle microscopique, dans le cadre de la théorie classique des stratifiés, les plis unidirectionnels sont supposés :

? Parfaitement liés les uns aux autres, c'est-à-dire que, entre eux il n'existe pas de glissement, ou décollement ;

? Avoir un comportement mécanique caractérisé par les déplacements ??₀(x, y, z, t), v₀(x, y, z, t) et ??₀(x, y, z, t) des points du plan moyen du pli ;

? Présenter un comportement élastique isotrope transverse ;

? Travailler en contraintes planes ;

1.2.2. Comportement mécanique d'une structure stratifié.

Compte tenu de ses hypothèses, le comportement mécanique est ainsi caractérisé à l'échelle du

pli par ses propriétés élastiques , , et . Pour un état de contraintes planes, la loi de Hooke

généralisée pour une couche k est traduite par :

'?xx? _{?Q:1 Q12 Q16???xx?}

? ? ? ? _{S S S} ? ? ? ?

_{xx 11 12 16 xx}

? ? ? ? ? ?
? ? _{S S S}

? ? ? ?

_{yy 12 22} 26 ? ? ?

_yy

_{16 26} 36 (1.2)

Q 66 ?

' ' ' ? ?? ? ? Q Q Q ? yy 12 26 ? ? yy ? 22 ' ' ' ? ? ? ? ? ? ? ? ? ? ? Q Q Q xy 16 26 ? ? ? ? ?xy k 66 k k Q ?

? ? ? ? ? ? ? S S S ? ? ? ? ? ? ? xy 16 26 66 k k xy k Ou

(1.1)

_Ca3C/33

Où Qae = Cap C représente les constantes de la matrice de rigidité réduite d'une couche k.

₃₃

¹¹ 1

_{LT LT}

_{LT LT}

- Sur les axes principaux, les composantes de la matrice de rigidité sont :

; ; ; ; ; ; ;

?? ? ₁ ?

? ?

Q et S étant des tenseurs inverses, il vient pour une structure orthotrope :

_?LTEL

Q12 ?

;

; (1.3)

_EL

; Q22 ?

_EL

₁

?

_VLTVLT

5

- En dehors des axes principaux :

Pour un composite unidirectionnel ou orthotrope, les constantes de rigidité en dehors de ses axes principaux sont exprimées par :

Chapitre 1 : Etat de l'art sur le comportement vibratoire d'un matériau composite

(1.4)

^Q = C4Q11 + _S4Q22 + ^2C2S2

¹¹

^Q2'2= S4Q11 + _C4Q22 + ^2S2C2

^Q

^_C2S2 66 - ^{Q12 =Q12(C4+S4)+(Q11+Q22-4Q66)C2S2}

Q;6=C3S( ^{-Q11+Q12+ 2Q66)+S3C(Q22-Q21-2Q66)} Q26 = S3C( ^-Q11 + ^Q12 + ^{2Q66)+ C3S(Q22 -Q21 -2Q66) (Q12 +2Q66)}

^{(Q12 +2Q66)}

( Q ^{11+Q 22-2Q} 12 -2Q ⁶⁶⁾⁺ Q ⁶ 6 (C ⁴ +S4)

Où : etS=Sin8

1.3. Formulation de la théorie classique des stratifiées

La théorie classique des stratifié nous permet d'établir les équations de mouvement d'une structure stratifié en se basant sur le modèle de Love-Kirchhoff ou de Mindlin. Mindlin dans sa théorie prend en compte le cisaillement transverse en supposant qu'une section effectue une rotation par rapport au plan moyen de la plaque tandis que Love-Kirchhoff rejoignent le modèle des plaques de Euler-Bernoulli qui ne tienne pas compte du cisaillement transverse. Ce dernier modèle sera retenu pour la suite de notre travail.

1.3.1. Hypothèses de Love-Kirchhoff

Le modèle de Love-Kirchhoff considère que [2] :

- La plaque est mince et L/h > 20 ;

- Les déformations et les déplacements restent petits (Hypothèse des petites perturbations) ; - Les interfaces entre les plis sont parfaites· ;

- Au cours de la déformation, les segments restent perpendiculaires à la surface moyenne, ce

qui permet de négliger l'effet du cisaillement transverse .

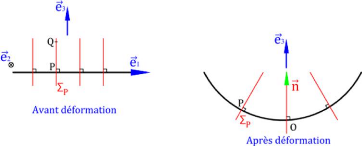
6

Figure 1.3 : Schématisation d'une plaque selon Love-Kirchhoff [2] 1.3.2. Expression du champ de déplacement cinématiquement admissible

Le champ général de déplacement en un point M d'une plaque de Love-Kirchhoff à l'instant t, s'exprime par :

7

Chapitre 1 : Etat de l'art sur le comportement vibratoire d'un matériau composite

_{v w} w 0

ÇO y

2 ? _{ö ö} ) ? _ö )

_{z y 2 y}

(1.5)

Où : et sont des déplacements membranaires dans les directions L et T ; et sont des

rotations dues à la flexion ; est la flèche de la plaque.

1.3.3. Expression générale du champ de déformation Le champ de déformation s'exprime par :

e yz = I + 1 = I + I

? ? ?

? ?

_{x y}

_{a w}

- ? -

? ₉

_{y x}

_{a y}

	·	(1.6)

(1.7)

(1.8)

(1.9)

(1.10)

(1.11)

Dans les conditions de Bernoulli-Euler qui ne tiennent pas compte du cisaillement transverse,

nous avons : . (1.12)
En reportant (1.12) dans (1.11) et (1.10), nous avons :

?w 0 ?x	0 (1.13)
En tenant compte de (1.13), (1.5), devient : ? ^wu x y t u x y tz x ^0 ( , , ) ( , , ) ? -- S = 0 S ^w ? ? ? ^v x y t v x y tz y ^0 ( , , ) = ( , , ) -- S S ^0 ? ? ^w( ^x, ^y, ^t) = w 0 ( ^x, ^y, ^t) ? ? En un point ??, le tenseur de déformation se traduit par l'expression : ? ? ? 0 ? ? ? ? xx xy xx ? ? ? ? ? ? ? ? ? 0 xy yy ? ? ? ? ? yy ? ? 0 0 0???? ? ? ? xy En tenant compte de (1.19), le tenseur de déformation peut se décomposer par :		(1.14) (1.15)

Chapitre 1 : Etat de l'art sur le comportement vibratoire d'un matériau composite

(1.16)

Il en ressort deux tenseurs des déformations représentant chacun :

n Le tenseur des déformations en membrane :

(1.17)

?? ?

^u0

? ?

?

? ? ? ? ?

^xx v

^{0 0}

^?m ? ^?yy ?

?0??

?

0??v

y

u

0

?? ? ? ?

^{0 x}

n Le tenseur des déformations en flexion et torsion :

^yy

^?f

??

(1.18)

? ? ? ?

y x ?? ? ^2w0 ? ? z?x2 ^{kxx ?z?k? ????z?2w0} ?y2 k ?????xy 2z ?2w0 ^?x?y

8

En posant 6 _f = zk , nous avons la matrice des courbures k . (1.19)

Finalement, le tenseur des déformations s'écrit :

(1.20)

1.3.4. Expression du champ de contraintes

En considérant (2.11), pour un pli k de normale ?? soumis à un état de contraintes planes, la loi de Hooke sur les axes du matériau s'écrit :

''

? ? ?

? _{Q Q Q}

' ? ? ?

?

' ' (1.23)

16 11 12 xx ? ? ? xx ? ? ? ' ' ' ? ? ? ? ? Q Q Q ? yy 12 26 ? ? yy ? 22 ? ? ? ' ' ' ? ? ? ? ? ? ? ? Q Q Q xy 16 26 ? ? ? ? ?xy k k 66 k ? ? Q ?m ? zQ k En tenant compte de (2.23), (2.24) devient : ' ' ' ' ? ? ? ? Q Q Q ? ? ? ? ?0 Q Q Q k ' ' ? ? ? xx 16 16 11 12 11 12 xx ? ? ? ? xx ? ? ? ? ? ? ' ' ' ? ? ? ? 0 ' ' ' ? ? Q Q Q z Q Q Q k 12 26 ? ? ? ? ? yy yy 12 26 ? ? ? yy 22 22 ? ? ? ? ? ? ? ? ' ' ' 0 ' ' ' ? ? ? ? ?xy 16 26 16 26 ? ? ? ? ? ? xy xy ? ? Q Q Q ? Q Q Q k ? ? ? ? k 66 k k k 66 k

(1.21) (1.22)

Chapitre 1 : Etat de l'art sur le comportement vibratoire d'un matériau composite

1.3.5. Expression des résultantes en membrane et des moments

Les différentes résultantes permettent d'établir l'équation constitutive d'un stratifié.

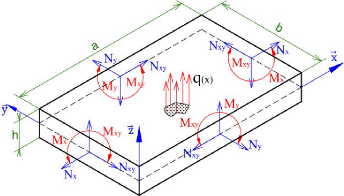
Figure 1.4 : Bilan des actions mécaniques appliquées à un élément de la plaque. > Les résultantes en membrane :

? ?

_N ? ?

?

_{xx xx}

n _h /2 ? ?

_N ? ? N ? ?

_{yy yy}

?? ? _dz

? ? _h /2 ? ?

?

_k ? ₁

? ?

_N ? ?

?

(1.24)

xy ? ?

? ? xy

(1.25)

_k

₀

? _{A A A} ?

_{11 12} 16 ? ? ? ? _{B B B} ? ? _k ?

_{xx 11 12 16 xx}

En associant (1.23) à (1.24), puis en intégrant, il vient :

₀

_N ? ? _{A A} A ? ? ? ? ? ? ?

? _{B B B k}

_{12 22} 26 ? ? ? ?

?

? _{yy 12 22} 26 ? ? ?

_yy

₀

? _{?A A A}

_{16 26} 66? ? ? ? ? ? ? ?

? _{B B B k}

_{xy 16 26} 66 ? ? ? ? ? ?

_xy

9

D'où : (1.26)

? ? h/2 ? ?

> Les moments de flexion et de torsion :

? ?

_M ? ?

?

_{xx xx}

M? M? yy yy ? z ? dz ? ? ? ? ?h/2 ? ? M ? ? xy ? ? ? ? ? xy k En reportant (1.23) à (1.27), puis en intégrant, il vient : B11 B12 B16 1??xx0 D11 D12 D16 1?k 1 M ??B12 B22 B26 ?ÿy ? D12 D22 D26 kyy B16 B26 B66 ?????xy0 ? D16 D26 D66 ????kxy ?

(1.27) (1.28)

D'où : _M = BEm + Dk (1.29)

Nous considérons que le stratifié est constitué de n couches, configuré comme le montre la figure

1.3.

10

Chapitre 1 : Etat de l'art sur le comportement vibratoire d'un matériau composite

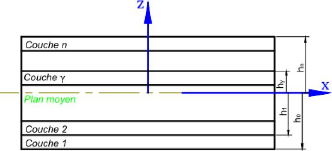
Figure 1.5 : Schéma d'un stratifié à n couches

_k=1 ?

Avec :

- : Représentent les coefficients de rigidité en membrane d'expression :

(1.30)

- : Représentent les coefficients de couplage membrane-flexion-torsion d'expression :

(1.31)

- : Représentent les coefficients de rigidité en flexion d'expression :

^n2hk D?? ? (Q l ao /k[hkzk ? 12

a,f =1,3,6 (1.31)

Avec : sont les coefficients de rigidité réduit, et sont respectivement la côte et

l'épaisseur de la couche ?? de n couches mesurée à partir du plan moyen.

1.3.6. Equation constitutive générale d'un stratifié en l'absence du cisaillement

Elle permet de lier les résultantes et les moments en fonction des différentes déformations. Pour cela, il suffit d'assembler (1.25) et (1.28) :

^N 1 ?A11 A12 A16 B11 B12 B16 1£ ^0 xx ? ? ? ? ? ? ^0 ? ? ? ^N A A A B B B£ ^yy 12 22 26 12 22 26? ^yy ? ? ? ? ? ?0 Nxy ? ^A16 A26 A66 B16 B26 B66 £xy ^M?B11 B12 B16 D11 D12 D16kxx ? ?? ^Myy? ?B12 B22 B26 D12 D22 D16 kyy ? ? ? ? ? ?M ^y^J B16 B26 B66 D16 D16 D66 ????kxy J

(1.32)

Du point de vue de l'équation constitutive, un composite est orthotrope si :

· Il n'existe aucun couplage membrane-flexion-torsion : _[B ] = [ 0] ;

· Il n'existe pas de couplage traction-cisaillement et flexion-torsion : _A16 = A26 = 0 et

D16=D16=0; (1.33)

Chapitre 1 : Etat de l'art sur le comportement vibratoire d'un matériau composite

Donc pour un stratifié orthotrope, l'équation constitutive est : ^0 ? ? ? ^N A A 0 0 0 0? ? ? ? ? 0 ^N 0 0 A 0 0 0? ? ^xy 66 xy ? ? ? ? ? ? ? ? ? ^M 0 0 00 ? ? ? ^xx 11 12? ? ? ^xx ? ? ? ^M 0 0 0 D D 0 ^1222 ? ? ? ^k ? ? ? ^yy yy ? ?? ^xy Q 66h D ? 66 12 ^xx 1112 ? ? ? ? xx ? ? ? ^?0 ^N A A 0 0 0 0? ? ? ? ^yy 1222 ? ? ? ? ? ^yy Cette équation est valable pour [3] : n Les plis unidirectionnels 0° et 90° de caractéristiques :

(1.34)

^{D D k}

Pour ; (1.35)

? ? ?

^M ? ^{0 0 0 0 0 D k}

66 ? ? ?

^xy ? ? ?

Pour ; (1.36)

n Les stratifiés symétriques à couches orthotropes dont les axes principaux coïncident avec les axes de références du stratifié : c'est le cas des stratifiés symétriques et antisymétriques. Les coefficients de rigidités de flexion s'expriment :

- Pour un stratifié croisé symétrique à n couches impaires :

_{1 R (n-3)[R (n-1)+2(n+1)1}

_{e e}

_a = +

( )

_{1+ Re}

; ;

r Q ³

_{D22 =[(1-RQ)a} + RQ1 r22h;

₁₂

₃

; (1.37)

³ _(n2 -1)(1+Re )3 ;

- Pour un stratifié croisé à n couches impaires :

₃

_D11= [(RQ-1)Q+1-1 12 ;

_D ? Q12h3

;

¹² 12

11

D22 = _{[(1-- RQ) fi} + _RQ '66 = ; Q22h3 _{D Q66h3} RR _Q = ET

(1.38)

12 12E.

_fi

; _{Re e0?}

_e90?

= 1 + 8Re(n-1) _1+R n2(1+R )3

Les études menées dans le cadre de cette recherche prendront uniquement en compte ce type de structures.

1.4. Comportement statique des matériaux composites orthotropes

Cette étude nous permettra de définir les différents paramètres de la flèche d'une structure orthotrope sollicitée en flexion.

Chapitre 1 : Etat de l'art sur le comportement vibratoire d'un matériau composite

1.4.1. Les différents paramètres de la flexion pure d'une plaque orthotrope

Considérons une structure composite orthotrope soumise à un chargement transverse q (x, y) et configuré comme le montre la figure ci-dessous.

_??divN ?

? _{2 2 2}

_u ? _u ? _v

_{0 0 0}

_A ? A ₂ ( 12

? _A ? A ₆₆ ) ? ₀

_{11 2 66}

? _x ? _y ? _x ? _y

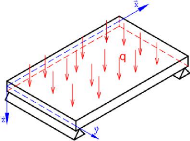
Figure 1.6 : Schémas d'une plaque pour flexion cylindrique.

Le comportement statique d'une telle structure est caractérisée par l'équation d'équilibre :

(1.39)

a _{2 2 2}

_{u a v a v}

_{0 0 0}

( 12

_A + A ₆₆ ) + _{A A} = ₀

_{66 2 22 2}

_{a x a y a x a y}

e _{4 4 4}

_{w e w e w}

_{0 0 0}

_D + _{2( 2} ) _{2 2}

_{11 4} 12 + =

_{66 22 4}

_{e x e x e y e y}

En l'absence des forces de volumes , il vient :

? _divM ???

_{D D} + _{D q}

	(a)

En développant l'équation constitutive, puis en reportant le résultat dans (a), il vient en l'absence des charges axiales :

? ?

_w ( _x , _y ) = ?? _{C k}

_{k=1 l=1}

(1.40)

(1.41)

_{x y}

qkl ? ₀

(1.42)

En flexion pure, l'équation d'équilibre est réduite à l'équation (1.42), donc la solution recherchée

pour une plaque en appuis simples est de la forme :

₁₆ q 0

^kl kl? ²

(1.43)

_qkl

?

Avec :

_Ckl

?

₂

(1.44)

_{4 2 2 4}

? ?

_k

? ? ? ₂ ? ?

₁₁ 12 ? ? ? ? ? ? ? ?

? ? ? ? ? ?

_{k l l}

_{D D 2 D D}

_{66 22}

? ?

_a ? ? ? ? ? ?

_{a b a}

12

q? Et :

, si et sont impairs ; (1.45)

, si et sont pairs.

Le comportement de la flèche en un point M (x, y) de la plaque s'écrit :

13

Chapitre 1 : Etat de l'art sur le comportement vibratoire d'un matériau composite

(1.46)

Avec : (1.47)

a _{2 2 3}

_{U a V a W}

_{0 0 0}

_A ? _A ? _B - ₀

Et : (1.48)

_{11 2 16 2 12 3}

_{a x ax ax}

1.4.2. Les différents paramètres de la flexion cylindrique d'une structure orthotrope

En flexion cylindrique, la déformation de la plaque est considérée comme indépendante de la coordonnée suivant la longueur de la plaque.

Configuration de la plaque en flexion cylindrique

Considérons une plaque stratifiée à n couches très longue suivant y, soumise à une charge transversale ??, configurée comme le montre la figure ci-dessous.

a _{2 2 3}

_{u a v a w}

_{0 0 0}

_A ? _A ? _B = ₀

_{16 2 66 2 16 3}

_{a x a x ax}

a _{4 3 3}

_{w a u a v}

_{0 0 0}

_D -- _B -- _B = _q

_{11 4 11 3 16 3}

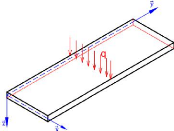
Figure 1.7 : Schémas d'une plaque pour flexion cylindrique. Les équations d'équilibres en l'absence des charges axiales sont dans cas :

_{a x a x a x}

₀₍ ) m cos

_{w 0( x} )

₀₍ ) m cos

u x A ? m ? 0( ) m cos v x B ? m ?

(1.49) (1.50)

_x

(1.51)

Pour une poutre en appuis simples, les solutions générales de cette équation sont de la forme :

(1.52)

_{w x C}

? _m ?

_a

_x

_a

_x

_a

(1.53)

(1.54)

Où est la flèche recherchée, ?? est la fréquence angulaire et est la déformée modale.

En flexion pure, il vient :

?

_{w 1}

0 ?

_q

_{x D}

? 11

_{4 4} (1.55)

14

Chapitre 1 : Etat de l'art sur le comportement vibratoire d'un matériau composite

Expressions de la flèche

En considérant qu'il s'agit d'une structure orthotrope, la résolution de l'équation (1.55) donne

l'expression de la flèche dans le cas d'un chargement :

(1.55)

? Pour une plaque en appuis simples sur ses extrémités :

(1.56)

? Pour une plaque Encastrées sur ses extrémités :

(1.57)

? Pour une plaque Encastrées et en appuis simples sur ses extrémités :

(1.57)

1.5. Comportement vibratoire des matériaux composites

Une structure composite vibrant et sollicité en flexion est toute structure qui se déforme transversalement en l'absence des phénomènes de couplage membranaire-cisaillement, flexion-torsion et ceux du couplage membrane-flexion-torsion.

1.5.1. Notion de la flèche

La flèche est le déplacement maximal qu'un point M de la structure considérée peut atteindre au cours des déformations temporaires de ladite structure. Le comportement de la flèche est observable à partir de l'évolution de la déformée. Il est donc clair qu'elle résulte du déplacement transversal. Ce dernier est issu de l'équation de mouvement d'un matériau sollicité soit en flexion soit au flambement, etc.

1.5.2. Les types de flèches

Après analyse des articles consultés, il en ressort que les flèches peuvent être regroupées en deux grandes familles :

- Les grandes flèches : observables lorsque le matériau est sollicité en flexion composée ou au flambement ;

- Les petites flèches : observables lorsque le matériau est sollicité en flexion pure. Dans le cadre de cette recherche, nous analyserons analytiquement le cas des petites flèches issues de la vibration en flexion pure.

1.5.2.1. Analyse à partir des vibrations d'une poutre
a) Poutre en matériau isotrope

15

Chapitre 1 : Etat de l'art sur le comportement vibratoire d'un matériau composite

Le premier dispositif expérimental a été développé par Adams et A. Fox [4J et, Adams et Bacon afin d'évaluer l'amortissement des composites. Ce dispositif permet d'étudier l'amortissement en flexion des poutres dans un domaine de fréquence allant de 100 à 800 Hz et a été utilisé dans le cas de différents stratifiés [5- 6J.

b) Poutre en matériau composite

Bien que les poutres homogènes isotropes soient la base de la théorie des poutres, les poutres non-homogènes et/ou non-isotropes sont d'une grande importance. (Cedi & Delhi, 2005) ont développé un modèle linéaire pour des poutres non-homogènes présentant une courbure dans un

1.5.2.2. Analyse à partir des vibrations des plaques et coques

Malgré l'intérêt particulier sur les poutres continuent, les plaques et les coques reçoivent également beaucoup d'attention. La caractéristique des plaques est que l'une de leurs dimensions est plus faible que les deux autres. Cette caractéristique est valable pour les coques, mais dans un repère d'axes curvilignes.

Il existe deux types de plaques :

? Les plaques épaisses ou les plaques de Mindlin ;

? Les plaques minces ou les plaques de Love-Kirchhoff.

a) Cas des plaques en matériaux isotropes

(Cheung & Zhou, 2000) ont utilisé la méthode de Rayleigh-Ritz afin de résoudre des problèmes de plaques de Mindlin homogènes isotrope, grâce à des fonctions modales de Timoshenko « statiques ». Les mêmes auteurs ont par la suite étendu leur recherche sur les plaques de Mindlin homogènes isotropes fuselées (Cheung & Zhou, 2003).

(Y.-S. Lee & Lee, 1997) ont calculé la réponse temporelle de plusieurs coques cylindriques en composites multicouches simplement supportées pour plusieurs cas de chargement transverses, grâce à la théorie des plaques du premier ordre. Les résultats ont été validés grâce au logiciel ABAQUS.

b) Cas des plaques en matériaux composites

(Gong et al., 1999) ont étudié les réponses vibratoires de plaques cylindriques monocouches et multicouches suite à des impacts à basse vitesse en utilisant la théorie de déformation en cisaillement d'ordre supérieur « Higher order Shear Deformation Theory ». Les matrices de rigidité utilisées sont les mêmes que des matériaux isotropes à l'exception que la valeur des composantes varie à travers l'épaisseur.

(Vo & Lee, 2008a) ont développé un modèle vibratoire de poutres minces laminées orthotropes à section creuse sur la base de la théorie des plaques de Kirchhoff-Love qui prend en compte le couplage des modes de flexion et les modes de torsion et qui est calculé par éléments finis.

(Qatu & Iqbal, 2010) ont utilisé le modèle de poutres d'Euler-Bernoulli pour calculer les fréquences propres d'un système de deux poutres cylindriques en composites orthotropes articulées

16

Chapitre 1 : Etat de l'art sur le comportement vibratoire d'un matériau composite

entre elles et simplement supportées à leur deuxième extrémité et possédant des masses concentrées sur l'articulation.

1.6. Méthodes de résolution et théories des problèmes de vibration

(Han, Benaroya, & Wei, 1999) ont comparé³ les 4 théories les plus utilisées en ce qui concerne les vibrations transverses : les modèles adimensionnels des poutres d'Euler-Bernoulli, de Rayleigh, de la poutre de cisaillement et de Timoshenko.

La différence entre le modèle de Rayleigh par rapport à celui d'Euler-Bernoulli est qu'il prend en compte l'inertie de rotation, le modèle de la poutre en cisaillement prend en compte le cisaillement transversal et le modèle de Timoshenko prend en compte les deux. Les hypothèses de base de ces théories sont que l'effet Poisson est négligé et que les sections des poutres étudiées possèdent deux axes de symétrie. Ce dernier est le modèle le plus précis des quatre énoncés. Les auteurs ont déterminé que lorsque le coefficient d'élancement (« slenderness ratio ») est supérieur à 100 le modèle d'Euler-Bernoulli convient bien pour les calculs. Sinon, les modèles de Timoshenko ou de la poutre de cisaillement devraient être préférés.

Les structures étudiées dans le cadre de cette recherche possèdent un coefficient d'élancement supérieur à 100. Donc, le modèle de Euler-Bernoulli est retenu pour la modélisation du comportement vibratoire transversal.

1.7. Cadre de validité de la recherche

1.7.1. Problématique de la recherche

Dans les challenges des diverses réalisations de haute technologie du monde, l'utilisation des matériaux composites est en pleine essor et devient peu à peu incontournable. Ainsi, les métaux se font substituer par des matériaux composites aux propriétés fascinantes, comblant les besoins impérieux de légèreté, rigidité et résistibilité avec un bon comportement à la fatigue tout en offrant la possibilité de concevoir et de façonner le matériau selon la nécessité. Cette constitution particulière des composites peuvent conférer un caractère biodégradable dans le cas où les constituants même le sont ; dans ce cas, leur utilisation est idéale pour des nouvelles conceptions visant à protéger et à respecter l'environnement.

. L'analyse vibratoire est une thématique actuelle importante, tant sur le plan académique qu'industriel. Cette dernière touche de nombreux domaines, notamment l'automobile, la marine, l'aéronautique, l'aérospatial, l'Architecture, les sports, la défense, l'industrie lourde et le textile. Le contrôle des vibrations dans les matériaux composites est un problème épineux qui se pose fréquemment aux chercheurs. Le domaine des vibrations connait depuis des années un regain d'intérêt du fait du besoin d'optimiser et d'alléger les structures couramment utilisées soumises à des niveaux d'excitations importants. C'est pour cette raison que le comportement des matériaux composites est depuis le sujet

³ La comparaison a été effectuée pour résoudre les problèmes des vibrations libres et forcées pour des conditions aux limites variées grâce au principe de Hamilton.

17

Chapitre 1 : Etat de l'art sur le comportement vibratoire d'un matériau composite

des recherches exhaustives. De plus, au Cameroun, en particulier au Génie Mécanique de l'ENSET, au Laboratoire de Mécanique des matériaux (LAMMA) et Laboratoire de Mécanique Et Productique (LMP) de l'UFD, les composites se font développer, mais une véritable modélisation comportementale n'est pas encore effectuée. Notre travail constituera en partie à étudier le comportement de ces composites, essentiellement l'aspect vibratoire.

En effet, Les vibrations produites par une structure peuvent avoir des causes variées, dont certaines inhérentes au processus du principe de fonctionnement de la machine. Le calcul vibratoire des matériaux composites constitue l'une des applications les plus utiles de la théorie des vibrations. Cette étude, peut particulièrement s'appliquée au cas des panneaux de signalisations et publicitaire. Ceux-ci s'endommagent souvent sous l'effet de la fatigue et des vibrations engendrée par les forces générées par le vent. Ces panneaux sont en général faits en métaux, ce qui leur rend lourd, ne leur confère pas un caractère non biodégradable et difficile à installer. Donc, l'une des applications de ceux travail est de substituer ces métaux par des composites légers, biodégradable susceptible de s'adapter aux vibrations présentent sur ladite structure. Il sera question d'interpréter la variation de la déformée modale d'un matériau composite en fonction des différents modes d'excitation.

Figure 1.8 : Images de quelques structures soumises aux vibrations [8-9-10]

1.7.2. Couplage vibratoire

Une des hypothèses de cette recherche est qu'il n'existe pas de couplages vibratoires avec les vibrations transversales. En effet, la déformation transversale lors d'une flexion sur un pli unidirectionnel (0° ou 90°) ou un stratifié orthotrope croisé possédant une séquence d'empilement symétrique ou antisymétrique dont les axes coïncident avec les axes du stratifié n'est pas couplée avec une déformation longitudinale. Pour éviter une possibilité de couplage, seul les structures mentionnées ici, seront pris en compte par le code développé.

18

Chapitre 1 : Etat de l'art sur le comportement vibratoire d'un matériau composite

1.7.3. Code de calcul développé

Le code développé dans le cadre de ce mémoire est basé essentiellement sur la théorie classique des stratifiés. Cependant, certaines hypothèses simplificatrices ont été adoptées afin de s'assurer de bien maîtriser le code et de bien comprendre les phénomènes physiques qui s'y déroulent.

Le code construit traite uniquement les vibrations transversales mais ne prend pas en compte les vibrations longitudinales, l'effet Poisson, ni le cisaillement, ni les couplages de torsion. Ceci induit des hypothèses menant sur le type d'élément que le code peut traiter, pour que la torsion et le cisaillement n'apparaissent pas. En effet, le code utilise des plis unidirectionnels ou orthotrope à 0° et 90°, et des stratifiés croisés symétriques ou antisymétriques bidirectionnels de [0/90].

1.7.4. Objectif de la recherche

L'objectif de cette recherche est de modéliser les vibrations transversales d'un composite répondant aux hypothèses de la théorie des plaques de Love-Kirchhoff et aux hypothèses de Euler-Bernoulli tout en tenant compte des modèles d'homogénéisation à « bornes » de Voigt et Reuss. Le paramètre à évaluer dans cette modélisation est la flèche et pour cela, il faut précisément :

? Développer un modèle théorique de calcul de la flèche et l'implémenter dans Matlab ;

? Simuler le comportement de la flèche des poutres et des plaques composites dont les caractéristiques des constituants sont connues ;

? Valider le modèle théorique par une comparaison avec les résultats de la simulation du comportement de la flèche des poutres et des plaques composites sous Abaqus ;

? Réaliser une analyse des résultats en mettant en exergue l'influence des différents paramètres des structures composites comme : la longueur, la hauteur, le taux de fibres et le module d'Young des fibres dans le comportement de la flèche et proposer des applications ;

En effet, la plupart des études s'arrêtent à l'analyse des fréquences propres et ne s'intéresse pas au comportement de la flèche qui d'ailleurs est un paramètre important pour le constructeur dans la conception des édifices.

Les paramètres principaux du problème sont les conditions limites de la poutre, les dimensions géométriques de chaque couche, les matériaux utilisés et la séquence d'empilement. Les paramètres qui traduisent les propriétés des matériaux utilisés sont les modules de rigidité et les coefficients de Poisson. Les modules de rigidité sont calculés grâce à la rotation des matrices de souplesse de chaque matériau dans ses axes principaux, autour de deux axes. Les paramètres géométriques sont la longueur de la poutre, son aire et son second moment de surface.

1.7.5. La méthode mathématique utilisée dans le cadre de la recherche

Bien que plusieurs méthodes existent pour résoudre le problème, tel qu'exposé dans la revue de littérature, les méthodes de séparation des variables, de Rayleigh et de Rayleigh-Ritz sont retenues.

19

Chapitre 1 : Etat de l'art sur le comportement vibratoire d'un matériau composite

La méthode de séparation des variables permet de résoudre une équation différentielle à plusieurs variables. Elle est valable uniquement pour des structures en appuis simples.

La méthode de Rayleigh-Ritz est sans aucun doute la méthode la plus simple puisqu'elle conduit à des formules polynomiales pour les fréquences propres. L'idée fondamentale de cette méthode est de

donner une forme approchée de la déformée modale d'une plaque en utilisant des résultats des

poutres. La méthode de Rayleigh sert à calculer la plus petite fréquence appelée « Fréquence fondamentale" en supposant que le déplacement w0 est égal au produit d'une fonction de déplacement.

Parvenue au terme de cette revue bibliographique dont l'objectif était de mettre en revue les matériaux composites et leurs comportements, force est de constater que la constitution exceptionnelle d'un matériau composite lui confère des performances mécaniques importantes devant celles des matériaux homogènes. Toutefois, ces performances en comportement mécanique dépendent des paramètres comme : l'orientation des fibres, la nature du renfort, le type de sollicitation, la fréquence de sollicitation, la masse volumique du composite, les déplacements en fonction des conditions aux limites. Variés et façonnables au gré, les matériaux composites vont droits aux désirs des concepteurs dans les domaines tels que : l'aéronautique, l'espace, l'automobile, etc. Ces domaines très sensibles exposent les composites à plusieurs comportements, notamment celui des vibrations. Parmi cette foultitude de composites, notre analyse théorique s'appuiera sur des plis et stratifiés orthotropes croisés dont les axes des couches coïncident avec les axes du stratifié suivant le modèle d'homogénéisation de Voigt et Reuss. Dans la même analyse bibliographique nous avons présenté la notion de flèche et les différentes méthodes de résolution d'un problème vibratoire. Seules des vibrations transverses en flexion pure seront traitées. Cette analyse se fera par le biais de la TCS qui formule les équations de mouvement d'un stratifié pris comme modèle des plaques de Love-Kirchhoff. Cette théorie sera transposée sur les poutres répondant aux hypothèses de Euler-Bernoulli. La résolution des différentes équations se fera au moyen des méthodes de séparation des variables et la méthode de Rayleigh-Ritz sur les différentes conditions aux frontières. Dans la suite de ce travail, il sera question de formuler les équations de comportement de la flèche d'un pli orthotrope et d'un stratifié orthotrope.

CHAPITRE 2 : FORMULATION THEORIQUE DE L'EQUATION DE COMPORTEMENT DE LA FLECHE EN VIBRATION DE FLEXION D'UNE STRUCTURE ORTHOTROPE

Chapitre 2 :
FORMULATION THEORIQUE DE L'EQUATION DE
COMPORTEMENT DE LA FLECHE EN VIBRATION DE
FLEXION D'UNE STRUCTURE ORTHOTROPE.

Les vibrations sont omniprésentes dans tous les équipements du secteur industriel provoquant parfois un disfonctionnement de la machine. Ainsi, les vibrations mécaniques doivent être prises en charge au cours de la conception des matériaux avant d'être mis en application dans la conception des structures. Le présent chapitre, a pour objectif de formuler l'équation générale du comportement de la flèche d'une poutre et d'une plaque d'un matériau composite de type pli unidirectionnel ou orthotrope et stratifié croisé symétrique ou antisymétrique. Pour y parvenir nous allons d'abord ressortir l'équation de mouvement d'un stratifié dans le cas de la flexion d'une plaque de Love-Kirchhoff puis sur une poutre de Euler-Bernoulli en nous appuyant sur la théorie classique des stratifiés, ensuite résoudre cette équation par la méthode de séparation des variables et la méthode de Rayleigh-Ritz, et enfin donner l'expression de la flèche pour chaque condition aux limites.

Chapitre 2 : Formulation théorique de l'équation de comportement de la flèche en vibration de flexion d'un composite

2.1. Définition des paramètres du problème.

Les structures composites traitées dans le cadre de notre travail sont des plaques minces de Love-Kirchhoff et des poutres en l'absence des couplages membrane-flexion-torsion.

? _v ( _x , _y , _t ) ? ? _z ? x

? ( , , ) ? ( , , )
? _{w x y t w x y t}

2.1.1. Champ de déplacement cinématiquement admissible du problème

La structure ne subissant aucun comportement en membrane, nous avons :

?

_{u (x, y, t)} ? _?z?y

₀

;

?

Il vient : (2.1)

2.1.2. Champ de déformation

Le champ de déformation prend uniquement des déformations de courbures dues à la flexion.

^f

?? 2w0

? ? 2

? ?

? ^?2w0

z x

? ?

?

?

(2.2)

21

^zk ?? z y2

? ?

? ² w

? ? ? ? ? ?

2z ^{x y}

??? ? ?

?

?

? ?

0 ? ? ?

2.1.3. Champ de déformation

La loi de Hooke à l'échelle du pli k, se réduis à l'expression :

_{Q:2Q161 k 1}

_a = zQ'k =z[Q:1

₂

xy

_{Q16 Q}

_{6 Q66} Jk ^k J

k

_{Q12 Q22 Q26} kyy (2.3)

2.1.4. Equation constitutive et condition d'équilibre dynamique de la structure L'équation constitutive prend en compte les efforts appliqués à la structure. Dans notre cas, nous avons à l'échelle du stratifié :

_{?M 1 ?D D D 1 ?k 1}

_{xx 11 12 16 xx}

? ? ? ? ? ?

(2.4)

(2.5)

_M ? _{?Myy D12 D22 D26 kyy}

_{??Mxy ???D16 D26 D66 ????kxy} ?

En développant, nous avons :

M =

_{xx 11 xx 12 yy 16}

_{M =Dk} +Dk +Dkxy _M = _{D k} + _{D k D k}

_{yy 12 xx 22} yy + _{26 xy}

_M = _{D k} + _{D k} + _{D k}

_{xy 16 xx 26 yy 66 xy}

Chapitre 2 : Formulation théorique de l'équation de comportement de la flèche en vibration de flexion d'un composite

En l'absence des charges transversales , et des forces de volumes, l'équation d'équilibre

dynamique est :

(2.6)

D'où : (2.7)

a _{4 2}

_{w a w}

_{0 0}

_D ? ? ₀

_{a a}

_{x t}

Il vient :

(2.8)

Cette équation est celle du mouvement transversal ou de la déformée d'une structure orthotrope ou unidirectionnelle.

2.1.5. Les différents problèmes de flexion à traiter

- En flexion pure d'une plaque orthotrope (en l'absence du couplage flexion-torsion,

), nous avons en l'absence des chargement axiaux ( ) :

_{11 4 s 2}

_/i

_{w 0( x} , _t ) ? _X ( _x ) _T ( _t )

Il vient : (2.9)

- Flexion pure des poutres orthotropes : Le problème est ramené sur les poutres en considérant que la flèche est fonction soit de x, soit de y (suivant la longueur de la poutre). Considérons dans notre cas que la flèche est uniquement fonction de x, il vient en l'absence d'une charge en membrane

⁴ a ²

_{a w}

+ = ₀

:

_{P a x a t}

(2.10)

22

La résolution de ces équations différentielles, donne l'équation de comportement de la flèche.

Cette résolution se fait au moyen des différentes conditions aux limites.

2.2. Vibrations en flexion pure des poutres orthotropes

L'équation qui décrit les déplacements dus aux vibrations en flexion dans une poutre est :

_{D w}

_{11 0 0}

_{4 2}

(2.11)

_s

_{D E} I ? + _ ?

_{X E I}

_{11 L xy} ?

_{f f} ( 1 _f ) _{m xy}

? _{X E}

? 2 ? ?

?

La solution générale recherchée de cette équation est de la forme :

_{p b b}

_s

a _{4 2}

_{X a T} (2.12)

? 2 ₄ . _T ? 2 . ₀

_X ?

_{a x a t}

En posant : (2.13)

En reportant (2.12) dans (2.11), il vient : (2.14)

Chapitre 2 : Formulation théorique de l'équation de comportement de la flèche en vibration de flexion d'un composite

En effectuant une séparation de variables dans (2.14), il vient : ??4 2 X ?? X ? ? ? x ?						(2.15)
D'où le système :			4 2 ??? ? ? ^2T ? 2 T 0 ? ? ?t2 ? ? 2 T ? 0	0	(2.16)
Avec :	? ? ?	0 1 2 3 4 T(t) = a sin wt + b cos wt (2.25) ? X (0) ? 0 X"(0) ? 0

_{I B} + _B = ₀

_{2 4}

?? -- _B + _B = ₀

_{2 4}

(2.26)

? Conditions aux limites :

En :

23

Résolution de l'équation (2.16a)

Soit : (2.16a)

Posons : (2.17)

La solution de (2.16a) est de la forme : (2.18)

En reportant (2.18) dans (2.16a), il vient : (2.19)

D'où : ; ; ; . (2.20)

(2.18) devient : (2.21)

Or : et (2.22)

(2.21) devient équivalent à : (2.23)
à déterminer avec des conditions aux limites.

Résolution de l'équation (2.16b) :

? 2 T ₂ ? _{t x} ? ₀

Nous avons : (2.16b)

La solution de (2.16b) est de la forme : (2.24)

Donc, il nous vient à expliciter les équations (2.23) et (2.24) en fonction des conditions aux limites.

2.2.1. Cas d'une poutre orthotrope en appuis simples (AA)

B 2 ? B 4 ? ₀

Figure 2.9 : Schéma d'une poutre en appuis simples sur ses deux extrémités ? ?

_w ( _x , _t ) = _X ( _x ) _T ( _t )

_X(x) = _{B sin 2 x} + _{B cos 2 x} + _{B sinh 2 x} + _{B cosh 2 x}

Chapitre 2 : Formulation théorique de l'équation de comportement de la flèche en vibration de flexion d'un composite

En :

(2.27)

(2.135) et (2.135) sous forme matricielle, donne :

(2.28)

Pour , nous avons : (2.29)

Il vient : (16) ; (2.30)
? Fréquence angulaire :

_{w 0( x ,0)}

(2.30) dans (2.17) : (2.31)

? Déformée modale :

1

_{w x} = _Ø 0 ( _,0) D _{m m}
? ? _{w x} =
Les relations (2.27) et (2.23) permettent d'écrire : 0 ( _,0) = _{C ?Ø 0 m m}

(2.32)

En posant : , la déformée modale (2.33)

Il vient : (2.34)

^a _{m ,r n ,r} [ =

_a / _{2; n m}

j _{sin x sin xdx} = ?

_{a a} ? ~

_{0; n m}

D'où : (2.35)

Avec : ; (2.36)

Déterminons et à partir des conditions de stationnarité :

? ? ?

_{C 0}

_{a a}

_n ? _m ? _n ?

_{w x xdx D}

0 ( _,0)sin ? ? _{sin x sin xdx}

_{a a a}

_{0 0}

?

2 ^a

_D ? ? _{w x}

_m ? xdx

_{a a}

₀

A

0 ( _,0)sin

_{m m} (2.37)

0 Or les déformées modales sont orthogonales, et : q 0 3 2 3 w x 0 ( ,0) ? ( x ? 2 ax ? a ) x

(2.38)

_m

Donc :

(2.39)

Où est la déformée en statique.

Pour une poutre orthotrope en appuis simples, nous avons :

_{q m} ?

_{0 3 2 3}

_D ? f ?

( _{x 2 ax} ? _a ) _{x sin xdx}

(2.40)

24

_a

Il vient :

(2.41)

Chapitre 2 : Formulation théorique de l'équation de comportement de la flèche en vibration de flexion d'un composite

· Equation de comportement de la flèche : Donc pour une poutre en appuis simples, nous avons :

(2.42)

Avec : ; (2.43)

1 7nTi n

_[A][B] =[ 0] (2.49)

Et : (2.44)

Cette équation de la flèche justifie le fait que, tous les modes se superposent au cours de la vibration d'une structure. Le mode fondamental correspond à m=1, de fréquence angulaire :

_{B B}

2 + 4

(2.45)

2.2.2. Cas d'une poutre orthotrope encastrées sur ses deux extrémités (EE) I L

_{w (x, t)} = _X(x)T(t)

_X(x) = _{B sin 2x+B cos 2x+B sinh2x+B cosh 2x}

_{1 2 3 4}

Figure 2.10 : Schéma d'une poutre encastrée sur ses deux extrémités

_{T(t)=asin at+b cos at}

_{l2 (B1 cos2a-B2 sin 2a+B3 cosh 2a+B4 sinh2a)}

Avec :

? I?

0

(2.46)

· Conditions aux limites :

_?X(0) = ₀

En :

_t

X'(0)=0 _{??/1,( -B1 +B3)}

_I?

₀

₀

_{B2? ?B4}

?

(2.47)

_B1

_B3

_B1

_r

_{sin 2a+B2 cos 2a+B3 sinh2a+B4 cosh2a} = ₀

₌₀

_?X(a)?0

En : tr(a)?0

(2.48)

(2.47) et (2.48)

sous forme matricielle, donne :

?^0 1 0 1?^B1??^0? ? ? ? ? ? ? ? ^0? 0 ? ? ? ? ^B0 ??? ^2 ? ^sin? ^a^cos? ^a^sinh? ^a^cosh ?aB ? ? ? ? ? ^0 ^3 ? ? ? ? ? ? ? ^?cos ?a?^?sin ?a ?cosh ?a ?sinh?a??^B4??^0? Pour [BIT * 0, nous avons : det(A) ? 0

Il vient : _{cos A,a} cosh Act=1 (2.50) Ani = _(m + 0.5)n-; ;mE

(2.51)

_a

· 25

Fréquence angulaire :

Chapitre 2 : Formulation théorique de l'équation de comportement de la flèche en vibration de flexion d'un composite

(2.51) dans (2.17) : (2.52)

· Déformée modale :

(2.48b), devient : (2.53)

D'où : (2.54)

sin 2a -- sink A,a

Il vient, pour le mode m :

(2.55)

Et : (2.56)

En posant : (2.57)

Il vient pour le déplacement transversal :

? ₀₍ ,) ?

(2.58)

Déterminons et

A t=0 jrw°(x'O)~~m (2.59)

m _{?m ?0}

C m

_{(n+0.5)ir (m+0.5)ir (n+0.5)ir}

? ? =

_{w0 (x,0)sin xdx} = D f _{sin x sin xdx}

₀ a _{o a a}
2 ^a

₀

_[af

(2.60)

Or les déformées modales sont orthogonales, et :

^a sin ^(m+0.5* _x sin ^(n+0.5* xdx

_{0 a a}

_[a/2;n=m

_j0;

_J

_n#m

(2.61)

_xdx

₀

Donc : _D ? _{?w0 (x,0)sin ?m}

_a

(2.62)

26

Où est la déformée en statique.

Pour une poutre orthotrope en appuis simples, nous avons : w0 (x,0) ? q0 (x2? 2ax ? a2 )x2 24D11 a Il vient : D ? q0 ? (x2 ? 2ax ? a2 )x2 sin mir 12aD11 0 a

(2.63) (2.64)

· Equation de comportement de la flèche :

Donc pour une poutre en appuis simples, nous avons :

_{w0(x, t)} ? _{E Dm} cos ?mt?m (x)(2.65)

_m

Chapitre 2 : Formulation théorique de l'équation de comportement de la flèche en vibration de flexion d'un composite

Avec : (2.66)

12aD11 0

Où : ; (2.67)

	;		· ' "" Et :

(2.68)

Cette équation de la flèche justifie le fait que, tous les modes se superposent au cours de la

vibration d'une structure. Le mode fondamental correspond à m=1, de fréquence angulaire :

?

?

_B ? _?B

_{2 4}

(2.69)

2.2.3. Cas d'une poutre orthotrope encastrée et libre (EL) _{w (x, t)} = _X(x)T(t)

_X(x) = _{B sin 2x+B cos 2x+B sinh2x+B cosh 2x}

_{1 2 3 4}

?

Figure 2.11 : Schéma d'une poutre en appuis simples sur ses deux extrémités I L

_{T(t)=asin at+b cos at}

X'(0)=0 _{ItA,(-B1 +B3)}

? I

_{(-B1 cos A,a+B2 sinA,a +B3 coshA,a+B4 sinhA,a)}

Avec :

? I?

0

(2.70)

· _r

₀

₀

?

Conditions aux limites :

?

_B1

_B3

_{B2 +B4}

_?X(0) = ₀

(2.71)

En :

?

?

?

?

?

_{A,2 (-B1 sin A,a} - _{B2 cos A,a} + _{B3 sinh A,a} + _{B4 cosh A,a)}

En :

₌₀

(2.72)

_I1A,3

_X"(a)?0

₌₀

_X"'(a)?0

27

(2.71) et (2.72) sous forme matricielle, donne :

?^0 1 0 1? ? ^B1??^0? ? ? ? ? ? ? ^?0? ^0? ?B2 ? 0 ^2 2 2 2 ? ?? ^sin? ^a?? ^cos?a? ^sinh? ^a? ^cosh ?aB ? ? ? ? ? ^0 ^3 ? ? ? ? ? ? ^3 3 3 3 ??? ^cos?a? ^sin? ^a? ^cosh? ^a? ^sinh?a ^??^B4?^?0?

[A][B] =[o](2.73)

Pour [BIT * 0 , nous avons : det(A) = 0 (2.74)

Il vient : _{cos Act} cosh il a = -1 (2.75) _Am = _(m - 0.5) g ; (2.76)

· Fréquence angulaire :

Chapitre 2 : Formulation théorique de l'équation de comportement de la flèche en vibration de flexion d'un composite

(2.17) dans (7) :wm= · Déformée modale :

2 _ (2.77)

Par un raisonnement analogue au précédent, il vient, pour le mode m :

[ _a/2;n=m

(2.78)

Et : (2.79)

En posant : (2.80)

Il vient pour le déplacement transversal :

(2.81)

Déterminons et

_a

_{w x xdx} ? _D

0 ( ,0)sin ? _{sin x sin xdx}

_{0 0}

At=01 2 ^a

mTin a a a ? x3-4ax-18a2?x2

(2.82)

?n?0.5?? ^a _{?m?0.5?? ?n?0.5??}

_m

₀

?

?

? Cm

?

(2.83)

Or les déformées modales sont orthogonales, et :

asin(m-0.5) 7rxsin(n-0.5)7rxdx

_{0 a a}

_{j0; n} # _m

_J

(2.84)

_xdx

₀

Donc : _D ? _{?w0 (x,0)sin ?m}

_a

(2.85)

28

Où est la déformée en statique. Pour une poutre orthotrope en appuis simples, nous

12aD11 ₀

avons :	q0 __ w0 (x) 24D11	a			(2.86)	Il vient : D = q0 f (x3-4ax-18a2)x2
Om (x)dx (2.87)

· Equation de comportement de la flèche :

Donc pour une poutre encastrée-libre, nous avons :

_w0(x,t) ? _?Dm cos ?mt?m(x)(2.88)

_m

_a

Avec : _Dm = q0 f (x3 -- _4ax --18a2) x²O_m (x)dx (2.89)

_12aD110

sinh Am -- sin Am Où : Om(x)= (cosh ilmx-- cos flmx)--ym(sinhilmx-- sin ilmx) ; 7m = COSh iim + cos m

;(2.90)

29

Chapitre 2 : Formulation théorique de l'équation de comportement de la flèche en vibration de flexion d'un composite

Et : (2.91)

Cette équation de la flèche justifie le fait que, tous les modes se superposent au cours de la vibration d'une structure. Le mode fondamental correspond à m=1, de fréquence angulaire :

(2.92)

Les expressions de D11 sont données dans (1.35) et (1.37) en fonction du type de structure. 2.3. Expressions explicites de la flèche d'une plaque stratifiée orthotrope

L'équation qui décrit les déplacements dus aux vibrations de flexion dans la plaque est :

					(2.93) (2.94) (2.95) (2.96) (2.97)	La solution recherchée est de la forme : Posons : ; ;
1 ^Y
		4

2.3.1. Cas d'une plaque orthotrope en appuis simples (AAAA)

Considérons une plaque en appuis simples configurée comme le montre la figure ci-dessous :

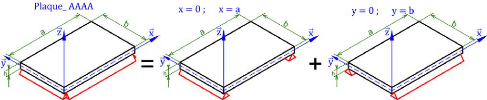
Figure 2.12 : Plaque rectangulaire en appuis simples sur ses 4 côtés (AAAA)

Résolvons (2.97a) : Posons _{Xm (x)} = sin m? x (2.98)

_a

ax ⁴ _{a a}

a2 mn ^2 mn D'où : 2 = sin x , ax a a

4 4 a X_ mr sin m r x (2.99)

_(m?

⁴ 2? ^{2 2} _{1 a2Y??2} ?4Y 1??4 2.100

a) Cam2r ) Yax2????y4.Y (2.100)

Chapitre 2 : Formulation théorique de l'équation de comportement de la flèche en vibration de flexion d'un composite

~Y4 -2~₂I _a I _axe +I I I -"_JY=O (2.101)

l J _zLl J

Posons à nouveau : ~z (2.102)

4 1² 2 ⁴

Il vient : (2.103)

a ôx a J

_[?B2 +B4 = B₂ =B₄ =O (2.109)
Les solutions de (2.103) sont de la forme :

(2.104)

Après résolution de (2.104), il vient :

a₁ = û₁ ; ; ; (2.105)

2 4 2 4

Avec : û1 = k2 m~ + m~ + ⁴ ; ₀₂ - k2 m7r - ^7717r + iî ⁴ (2.106)

_{a a a a}

Donc : (2.107)

Ou (2.108)

B₁, B₂, B₃, B₄ = ctes à déterminer avec des conditions aux limites.

? _X(a)?0

_{lO (_B1sinO2b_B2cosO2 b)+O12(B3 sinh O1 b+B4 cosh O1b)}

· Conditions aux limites :

En : ?X(0)=0 =

_-02B2+01B4=0

_jX"(0) = ₀

En : 1X"(a)?0

?? _{B1 sinO2b+B1 cosO2b+B3 sinhO1b+B1 coshO1b} = ₀

₌₀

(2.110)

30

(2.109) et (2.110) sous forme matricielle, donne :

^?0 1 0 1? ? ^B1? ?0? ? ? ? ? ? ? ^?0? ^0 B2 0 ? ^sin? ^cos 2 ^b? ^sinh 2 ^b ?1 b cosh? ^0 1 ^b B ? ? ? ? ? ^3 ? ? ? ? ? ? ? ? ? ? ? ? ? ^2 2 2 2 ? ? ^cos a? ^cos inh cosh ^2 22 b ^11 ^b? ^11 b ? ^?B4? 0?

(2.111)

Pour ^[BIT 0, nous avons : (2.112)

Il vient : _{(û, +û2)2}

_sinhû1b sin 02b = 0 (16) ; (1.113)

? En tenant compte de (2.106), nous avons : 62n = _k2 m~ - m~ + ~;, =(fur (2.114)

· Fréquence angulaire :

_{2 4 2}

_{a a b}

_{2 212}

₂

D'où : ~_{4 k2(mir (rur} -(rmi - ^cons; (2.115)

_a b J _{a 82}

Chapitre 2 : Formulation théorique de l'équation de comportement de la flèche en vibration de flexion d'un composite

En développant (2.115), puis en posant , il vient :

(2.116)

? Déformée modale :

En tenant compte de (2.109), (2.110) et (2.108), il vient :

_{a b}

Y(y) = B_n Sin b y (2.117)

En posant : , la déformée modale (2.118)

a b

Les relations (2.98), (2.117) et (2.118) permettent d'écrire (2.94) :

Qmn= ₆₄ q0 z .

Il vient :

D'où :

Or :Jsin(2m sin(2k-Ondxfsin(2n-Onsin(21-1)ndy=~^;m=w; (2.119)

_mnab~ _(2m -1)(2n _{-1)D2m-1,2n-1} 0 ax

Par un raisonnement analogue à celui des poutres, nous avons : , et

¹ _Jsin2(2m-1)~_{xdxf sin2(2n-1)}~_ydy

₀

?

?

(2.120)

? ?

_{16 q 1}

₀

_{w x y} ?

0 ( , ) ? ₂ ??

_{mn (2 m} ? _{1)(2 n} ? _{1) D}

_x

_{sin 2 1}

? ? ?
_m? ? _{sin 2n?1}

?_y ? _{a b}

Avec :

?

?

?

(2.121)

_{4 2} 2 2 4 4

_{2 ?1 R}

_m ? _{1 n} ? _{1 2 m} ? _{1,2 n} ? ₁

_D ? _{D m}

? ? ?

_{2 ?1 ?2 D ?2D} ?? ? ? ?

_{2m?1 2n?1 R ?D} ? _n ?

_{2m?1,2n?1 11 12 66 22}

_{16 q0 1}

Donc, pour une plaque en appuis simples, nous avons :

_w0(x,y,t) = EE(Qmn cos Wmnt)bmn(x,y)(2.122)

_{m n}

Avec : _Q =

^mn _{mnr2 (2m} -1)(2n -1)D2m-1,2n-1

; (2.123)

Y'

31

/x, _Y) = sin ^mIr xsin b _sin xsinB (2.124)
mn\ a _{m znY
D2m-1,2n-1 =D11(2m-1)4+2(D12+2D66)(2m-1)2(2n-1)2R2+D22(2n-1)4R4(2.125)}

2 TC r Et : O)mn = 2 1 Lm4D11 + 2m2n2R2 (D12 + 2D66 ) a Ps

+ n2R4D22 ] (2.126)

Donc, la plaque vibre comme un assemblage complet de n poutres en appuis simples suivant y et de m poutres en appuis simples suivant x.

Chapitre 2 : Formulation théorique de l'équation de comportement de la flèche en vibration de flexion d'un composite

Pour les autres conditions aux limites, les fonctions X(x) et Y(y) seront choisie comme dans le cas d'une poutre en fonction des conditions aux limites. La méthode Rayleigh- Ritz permettra d'expliciter le déplacement transverse et par l'approximation de Rayleigh nous ressortirons l'expression de la fréquence propre pour un mode ????.

2.3.2. Approche par la méthode de Rayleigh

La résolution de l'équation (2.93) est très complexe pour des plaques dont les quatre côtés ne sont pas en appuis simples. L'approche vibrationnelle développée dans ce contexte par Rayleigh [11] permet de déterminer les fréquences propres avec une marge de 1% des valeurs réelles pour des plaques n'ayant pas de côtés libres et absence du chargement en membrane. Cette méthode considère que le système étudié est conservatif ^4.

2.3.3. Energie de déformation

L'énergie totale de déformation est exprimée par :

_U?

_{2 2 2}

? _{2 2 2 2 2}

₁ ? ? ? ? ?

_{a b w w w} ? ? ? ? ? ? ?

_{w w}

? _{0 0 0 0 0}

_{2 4}

? ? ₁₁ ? ₂ ? ? _{12 2 2 22 2 66 2}

_{D D} ? ? ? ? ? ? ?

_{D D dxdy}

(2.127)

En décomposant sur les axes de référence, nous obtenons :

(2.128)

En tenant compte des hypothèses de la théorie des stratifiées (azz = O,E_yz = E_zz = 0) et du fait

que le matériau est un stratifié orthotrope dont les axes coïncident avec les axes de références (D16 = D26 = ⁰) sollicité en flexion pure (6_z, = 0) , l'énergie de déformation a pour expression :

2 _x ? _{0 y} ? 0 ? ? ?

? ? _x ? _x ? y ? ? ? ? ?

? _y ? y ?

d

^(2.129) ? ? ? ? ? ? ? ? ? ? ? ? dxdydz ? t t t 2 2 2 1 u v w E C ? ? ? ? ? ? ? ? ? ? ? s 2 ? ? ? ? ? ? ? ? ? ? ? ? ? ?

2.3.3.1. Energie cinétique

L'énergie cinétique totale d'un solide s'écrit :

(2.130)

₁

32

En tenant compte des considérations d'études du §1.3, il vient :

2 _a fb 2

ECMax = 2 Psi _Jx=0 Jy=0 w0dxdy (2.131)

2.3.3.2. Formulation du théorème d'énergie en théorie des stratifiées

En l'absence de charge transverse q, la fonction énergie maximum pour un stratifié orthotrope est donnée par :

_{2 2 2}

? _{2 2 2 2 2}

? ? ? ?

_{1 a b w} ? ? ? ? ?

_{w w w} ? ? ?

_w

_{0 0 0 0 0 2 2}

_U ? _E ? ? _D ? ? ? ? ? ? ? _w ? _dxdy

₁₁ ? ? ? _{2 D D 4 D}

_{dMax CMax 2 12 2 2 22 2 66 2 s 0}

2 ? ? ? ?

_x ? _{0 y} ? 0 ? ? ?

? ? _x ? _x ? y ? ?

? y ? ?

? y ? ?

(2.132)

⁴ Système conservatif : Energie potentielle maximale = Energie cinétique maximale.

Chapitre 2 : Formulation théorique de l'équation de comportement de la flèche en vibration de flexion d'un composite

La fonction d'énergie est obtenue en posant :

Avec : (2.133)
La résolution de ce système [3J, donne l'expression de la fréquence angulaire :

Donc : _{w x y t} ? ?? _Q ? _t ? _{x y}

₀₍ , , ) ( mn cos mn ) mn ( ,

	(2.134)

33

Où les valeurs des coefficients C1, C2 et C3 sont fonctions des conditions aux appuis. [Annexe 1]. 2.3.4. Cas d'une plaque orthotrope à côtés encastrés (EEEE)

_cos ? i ? _cosh ? i

? ?

ⁱ _sin ? ? _sinh ? i

_i

_{m n}

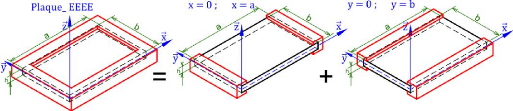
Figure 2.13 : Plaque rectangulaire encastrée sur ses 4 côtés (EEEE) Par analogie au cas d'une poutre encastrée à ses deux extrémités, nous avons pour :

? ?	Les côtés X = 0 et X = a encastrés : Les côtés y = 0 et y = b encastrés, nous avons : Où : Et			(2.135) (2.136) (2.137) (2.138a) (2.138b) (2.139)

)

2.3.1. Cas d'une plaque orthotrope à deux côtés opposés encastrés et les deux autres en appuis simples (AEAE)

Figure 2.14 : Plaque encastrée sur 2 côtés consécutifs et en appui simple sur les 2 autres (AEAE). Par analogie au cas d'une poutre encastrée à ses deux extrémités, nous avons pour :

? Les côtés X = 0 et X = a en appuis simples, nous avons :

Chapitre 2 : Formulation théorique de l'équation de comportement de la flèche en vibration de flexion d'un composite

				(2.83)
Les côtés y = 0 et y = b encastrés, nous avons :
		(2.84)
		(2.138)
	;
Donc :

Parvenue au terme de ce chapitre portant sur le calcul vibratoire en flexion d'un matériau composite, il est important de constater que l'objectif de la détermination des équations de comportement de la flèche a été atteint au moyen de la formulation de la théorie classique des stratifiés basée elle-même sur le modèle cinématique d'une plaque de Love-Kirchhoff. Cette théorie classique nous a permis de déduire l'équation de comportement de mouvement correspondant au mouvement transverse pour le cas d'une structure stratifié unidirectionnelle ou orthotrope sollicitée en flexion. L'extension de cette théorie sur la théorie des poutres nous a permis de ressortir l'équation des vibrations transverses d'une poutre. La solution de ces équations obtenue par la méthode de séparation des variables exprime la flèche recherchée en fonction de la déformée modale, de la fréquence angulaire et du temps. En considérant les différentes conditions aux extrémités, la condition de stationnarité⁵ et en tenant compte de la fonction d'énergie comme l'impose la méthode de Rayleigh-Ritz, nous avons ressortie l'expression explicite de la

fréquence propre pour un mode d'excitation. Cependant, l'effort de calcul au moyen d'une méthode
analytique manuelle est très important et prend beaucoup trop de temps. Raison pour laquelle, il sera question par la suite, d'implémenter ses équations dans le logiciel Matlab pour effectuer une simulation du comportement de la flèche.

34

5 Stationnarité : identifié ici par un flambement statique ou une flexion statique.

CHAPITRE 3 : SIMULATION NUMERIQUE SOUS MATLAB DU COMPORTEMENT DE LA FLECHE D'UNE STRUCTURE COMPOSITE.

Chapitre 3 :

SIMULATION NUMERIQUE SOUS MATLAB DU COMPORTEMENT DE LA FLECHE D'UNE STRUCTURE COMPOSITE

Les vibrations sont des oscillations ou des mouvements de va-et-vient très rapide. Cette définition est justifiée par les expressions complexes des fréquences angulaires propres et des équations de comportement de la flèche établies au chapitre précédent. Face à cette complexité, il est donc clair que la résolution analytique manuelle prendra beaucoup plus de temps et nécessitera effort de calcul très important. Pour remédier à cela, nous allons résoudre ces équations numériquement à l'aide du logiciel Matlab. Pour y parvenir, nous allons d'abord traduire les différentes équations en script, ensuite nous lancerons le calcul pour pouvoir visualiser numériquement et graphiquement les différents résultats et enfin nous une interprétation des différents résultats sera effectuer.

36

Chapitre 3 : Simulation numérique du comportement vibratoire d'une structure composite

3.1. Notion de simulation sous Matlab

MATLAB (MATrix LABoratory) est un puissant logiciel de développement et de programmation très avancé destiné aux chercheurs scientifiques, aux ingénieurs et étudiants de divers spécialités (Physique, Mécanique, Mathématiques, etc.).

3.1.1. Objectif de la simulation sous Matlab

Réaliser des simulations numériques basées sur des algorithmes d'analyse numérique. Il peut donc être utilise pour la résolution approchée d'équations différentielles, d'équations aux dérivées partielles ou de systèmes linéaires, etc...

3.1.2. Intérêt de la simulation sous Matlab

Matlab a été choisi dans le cadre de cette recherche parce qu'il permet de résoudre sous forme numérique des problèmes très complexes pouvant nécessiter de grandes puissances de calcul.

3.2. Présentation du composite étudié

Dans le cadre de cette étude, nous utilisons un matériau composite constitué d'une matrice polyester et renforcé par des fibres de RC (Rhectophyllum Camerunense) [12J. En effet, la matrice polyester est utilisé parce qu'elle est disponible en quantité dans le marché local et les fibres de RC parce qu'elles sont légères avec un grand module d'Young [1J.

Tableau 3.1 : Tableau des caractéristiques des constituants

Caractéristiques des constituants									Matrice Polyester
Fibres RC					[GPaJ
[GPaJ			[Kg/m^3J	[GPaJ	[GPaJ		[Kg/m^3J	2.8-3.6
1.40		0.4	1200	2.3-17	1.38-10.2	0.2	947

3.3. Programmation des équations de la flèche sous Matlab

Dans cette simulation, nous nous intéressons aux flèches maximales de la structure, pour cela, nous allons programmer sous Matlab, l'équation de comportement de la flèche pour une structure de type pli. Dans ce test il sera question d'évaluer pour un élément, la :

· Variation de la flèche maximale en fonction des dix premiers modes d'excitations ;

· Influence de la longueur de l'élément sur le comportement de la flèche maximale ;

· Influence de la hauteur de l'élément sur le comportement de la flèche maximale ;

· Influence du type de section de l'élément sur le comportement de la flèche maximale ;

· Influence du taux sur le comportement de fibres de la flèche maximale ;

· Influence du module d'Young sur le comportement de la flèche maximale.

37

Chapitre 3 : Simulation numérique du comportement vibratoire d'une structure composite

3.3.1. Présentation des éléments et des conditions aux limites de la simulation

Dans cette simulation, nous utiliserons des éléments de types poutre et plaque unidirectionnelle à 0°. Les conditions aux limites sont présentées dans le tableau ci-dessous :

Tableau 3.2 : Présentation des différentes conditions aux limites

Plaque
Plaque_AAAA
Poutres
Poutre_EE
Poutre_AA
Poutre_EL

3.3.2. Modélisation des éléments dans le cas de l'élément poutre

3.3.2.1. Cas d'une poutre EE

Dans ce cas, les poutres simulées sont prismatiques de dimensions 150x10x15 mm à section rectangulaire renforcées avec un taux X?? = 60%.

a) Variation de la flèche maximale en fonction des dix premiers modes d'excitations Présentation graphique des résultats

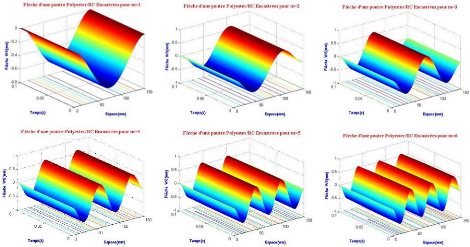
Figure 3.15 : Graphe de variation de la flèche maximale pour les 6 premiers modes

38

Chapitre 3 : Simulation numérique du comportement vibratoire d'une structure composite

Présentation numérique des résultats

Ces résultats présentent les valeurs des flèches maximales pour les différents modes. Tableau 3.3 : Valeurs des flèches maximales pour les 10 premiers modes d'une poutre EE

Flèche maximale d'une poutre composite encastrée en Polyester/RC
X 1 = 35% ; ; ; : rectangulaire ;150x15x15
Modes	1	2	3	4	5	6	7	8	9	10
Flèche (mm)	0,5830	0,5540	0,5552	0,5552	0,5552	0,5552	0,5552	0,5552	0,5552	0,5552

W0max (mm)

0,585

0,575

0,565

0,555

0,58

0,57

0,56

0,55

0,583

1 2 3 4 5 6

Mode "m"

0,554

0,5552

0,5552

0,5552

W0max=f(m)

Figure 3.16 : : Graphe de variation de la flèche maximale en fonction des modes

Le mode fondamental 1, présente la flèche maximale. Le mode 2 traduit le régime transitoire avec un pourcentage de chute de 4.97% du mode 1 ; le mode 3 et les autres modes traduisent le régime permanant avec un pourcentage d'élévation de 0,21% par rapport au mode 2 et un écart relatif de 4,76% avec le mode fondamental présenté comme le plus dangereux.

b) Influence de la longueur de la poutre sur le comportement de la flèche maximale.

Dans ce test il est question de faire varier la longueur « a » de la poutre, puis visualiser le comportement de la flèche.

Tableau 3.4 : Valeurs des flèches maximales avec différentes longueurs pour 5 modes d'une poutre EE.

Poutre EE	Composite : Polyester/RC						Xf = 0.35	Ef = 8.5
	Flèche maximale (mm)						q0 = 1N	h = 15
Modes	a = 80	a = 150	a = 250	a = 500	a = 750	a = 1000	Moyenne	Ecart type
1	1,0931	0,5830	0,3498	0,1749	0,1166	0,0874	0,41221667	0,39343837
2	1,0388	0,5540	0,3324	0,1662	0,1108	0,0831	0,39175	0,37389842
3	1,0411	0,5552	0,3331	0,1666	0.1110	0,0833	0,3926	0,37471908
4	1,0410	0,5552	0,3331	0,1666	0,1110	0,0833	0,39258333	0,37468447
5	1,0410	0,5552	0,3331	0,1666	0,1110	0,0833	0,39258333	0,37468447

39

Chapitre 3 : Simulation numérique du comportement vibratoire d'une structure composite

W0max (mm)

0,8

0,6

0,4

0,2

1,2

0

1

0 1 2 3 4 5 6

Mode "m"

a=80 mm a=150 mm a=250 mm a=500 mm a=750 mm a=1000 mm Moyenne

Figure 3.17 : Influence de la longueur de la poutre sur le comportement de la flèche

La flèche maximale croit avec la diminution de la longueur de la poutre. Car la période des oscillations augmente avec la longueur de la poutre. La figure ci-dessous présente une poutre de longueur 1000 mm excitée au 5^ème mode et le tableau présente les valeurs des fréquences pour différentes longueurs.

Figure 3.18 : Comportement de la flèche sur une poutre EE de longueur 500 mm

Tableau 3.5 : Valeurs des fréquences angulaires maximales avec différentes longueurs pour 5 modes d'une poutre EE.

Poutre EE	Composite : Polyester/RC					Xf = 0.35	Ef = 8.5
	Fréquence angulaire maximale (Rad/s)					g0 = 1N	h = 15
Modes	a = 150	a = 250	a = 500	a = 750	a = 1000	Moyenne	Ecart type
1	124,8	44,9	11,2	5,00	2.80	37,74	51,5456
2	499	179,7	44,9	2,00	11,2	147,36	209,0835
3	1122,8	404,2	101,1	44,9	25,3	339,66	463,7052
4	1996,1	718,6	179,7	79,8	44,9	603,82	824,3913
5	3118,9	1122,8	280,7	124,8	70,2	943,48	1288,0936

40

Chapitre 3 : Simulation numérique du comportement vibratoire d'une structure composite

ù0max (rad/s)

3500

3000

2500

2000

1500

1000

500

0

0 1 2 3 4 5 6

Mode "m"

a=150 mm a=250 mm a=500 mm a=1000 mm Moyenne a=750 mm

Figure 3.19 : Influence de la longueur de la poutre EE sur les fréquences angulaires propres Plus une poutre est longue, moins elle vibre. Donc, les poutres élancées ont tendance à absorber les vibrations.

c) Influence de la hauteur de la poutre sur le comportement de la flèche maximale.

Dans ce test il est question de faire varier la hauteur totale « h » de la poutre, puis visualiser le comportement de la flèche.

Tableau 3.6 : Valeurs des flèches maximales pour différentes hauteurs des 5 premiers modes d'une poutre EE.

Poutre EE	Composite : Polyester/RC					Xf = 0.35	Ef = 8.5
	Flèche maximale (mm)					g0 = 1N	a = 150
Modes	h = 10	h = 15	h = 20	h = 25	h = 30	Moyenne	Ecart type
1	1,9676	0,5830	0,2459	0,1259	0,0729	0,59906	0,79035
2	1,8698	0,5540	0,2337	0,1197	0,0693	0,5693	0,75105
3	1,8739	0,5552	0,2342	0,1199	0,0694	0,57052	0,75272
4	1,8738	0,5552	0,2342	0,1199	0,0694	0,5705	0,75267
5	1,8738	0,5552	0,2342	0,1199	0,0694	0,5705	0,75267

W0max (mm)

2,5

0,5

1,5

2

0

1

0 1 2 3 4 5 6

Mode "m"

h=10 mm h=15 mm h=20 mm h=25 mm h=30 mm Moyenne

Figure 3.20 : Influence de la hauteur de la poutre (EE) sur le comportement de la flèche.

41

Chapitre 3 : Simulation numérique du comportement vibratoire d'une structure composite

Lorsque la hauteur d'une poutre est grande, la structure devient de plus en plus rigide et provoque ainsi une diminution de la flèche maximale. La figure ci-dessous présente une poutre de hauteur 15 mm excitée au mode 5.

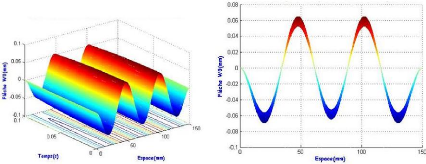
Figure 3.21 : Influence de la hauteur de la poutre (EE) sur les caractéristiques vibratoires.

Tableau 3.7 : Valeurs des fréquences maximales pour différentes hauteurs des 5 premiers modes d'une poutre EE.

Poutre EE	Composite : Polyester/RC				Xf = 0.35	Ef = 8.55
	Fréquence angulaire maximale (Rad/s)				g0 = 1N	a = 150
Modes	h = 8	h = 10	h = 12	h = 15	Moyenne	Ecart type
1	66,5	83,2	99,8	124,8	93,575	24,86260579
2	266,1	332,7	399,2	499	374,25	99,34433384
3	598,8	748,5	898,2	1122,8	842,075	223,5289299
4	1064,6	1330,7	1596,9	1996,1	1497,075	397,3689501
5	1663,4	2079,3	2495,2	3118,9	2339,2	620,8922988

ù0max (rad/s)

3500

3000

2500

2000

1500

1000

500

0

0 1 2 3 4 5 6

Mode "m"

h=8 mm h=10 mm h=12 mm h=15 mm Moyenne

Figure 3.22 : Influence de la hauteur de la poutre (EE) sur les fréquences angulaires.

42

Chapitre 3 : Simulation numérique du comportement vibratoire d'une structure composite

La fréquence angulaire croit avec l'augmentation de hauteur de la poutre. Plus une poutre est rigide et plus elle est sensible aux vibrations transversales.

d) Influence du type section d'une poutre sur le comportement de la flèche maximale.

Dans ce test, il est question d'analyser l'influence du type de section sur le comportement de la flèche d'une poutre. Pour y parvenir, nous modifierons l'expression du moment quadratique « 4 » caractérisant le type de section.

Tableau 3.8 : Valeurs des flèches maximales pour différents types de sections d'une poutre EE suivant les 5 premiers modes d'excitations.

Xf= 0.35	Ef= 8.5
q0= 1N	a= 150
Poutre EE		Composite : Polyester/RC
		Flèche maximale (mm)
		S_Rect.-P	S_Rect.C		S_Cir.-P	S_Cir.C	S_Car. -P	S_Car.C
Modes
1		0,5830	0,5830		0,5830	0,5830	0,5830	0,5830
2		0,5540	0,5540		0,5540	0,5540	0,5540	0,5540
3		0,5552	0,5552		0,5552	0,5552	0,5552	0,5552
4		0,5552	0,5552		0,5552	0,5552	0,5552	0,5552
5		0,5552	0,5552		0,5552	0,5552	0,5552	0,5552

Pour des poutres de section rectangulaire, carrée et circulaire, soumises à des vibrations, la valeur de la flèche maximale d'une poutre encastrée à ses deux extrémités n'a pas d'influence sur le comportement de la flèche. Donc la flèche d'une structure composite est liée aux caractéristiques des constituants. Néanmoins, nous observons une modification de la période d'oscillation.

Tableau 3.9 : Valeurs des fréquences maximales pour différents types de section d'une poutre EE suivant les 5 premiers modes d'excitations.

Poutre EE	Composite : Polyester/RC
	Fréquence angulaire maximale (Rad/s)
Modes	S_Rect.-P	S_Rect.C	S_Cir.-P	S_Cir.C	S_Car. -P	S_Car. -C
1	112,352	99,4807	86,2296	80,4481	79,4449	74,1183
2	312,0889	276,3353	239,5267	223,467	220,6802	205,8841
3	611,6943	541,6172	469,4723	437,9953	432,5332	403,5328
4	1011,2	895,3264	776,0665	724,033	715,0038	667,0645
5	1,51E+03	1337,5	1159,3	1081,6	1068,1	996,479
Moyenne	711,5675	630,052	546,112	509,5087	503,1525	469,416
Ecart type	560,5109	496,3102	430,1856	401,3528	396,3435	369,767

43

Chapitre 3 : Simulation numérique du comportement vibratoire d'une structure composite

ù0max (rad/s)

1600

1400

1200

1000

800

600

400

200

0

1 2 3 4 5

Modes "m"

S_Rect.-P S_Cir.-P S_Car. -P S_Rect.C S_Cir.C S_Car.C

Figure 3.23 : Influence du type de section d'une poutre (EE) sur les fréquences angulaires.

Donc, les poutres à sections rectangulaires ont des fréquences angulaires plus importantes que les autres sections, tandis que les poutres à sections carrées ont des fréquences propres moins élevées. e) Influence du taux de fibres sur le comportement de la flèche maximale.

Dans ce test, il est question de faire varier le taux de fibres d'une poutre et observer le comportement de la flèche.

Tableau 3.10 : Valeurs des flèches maximales pour différents taux de fibres d'une poutre EE suivant les 5 premiers modes d'excitations.

Poutre EE	Composite : Polyester/RC				a = 150
	Flèche maximale (mm)				Ef = 8.5
Modes	Xf= 0.25	Xf= 0.35	Xf= 0.50	Xf= 0.60	Moyenne mi
1	0,6515	0,5830	0,5053	0,4648	0,55115
2	0,6192	0,5540	0,4802	0,4417	0,523775
3	0,6205	0,5552	0,4812	0,4427	0,5249
4	0,6205	0,5552	0,4812	0,4426	0,524875
5	0,6205	0,5552	0,4812	0,4426	0,524875
Moyenne Xi	0,62644	0,56052	0,48582	0,44688
Ecart type	0,0141	0,0126	0,011	0,010026

w0max (mm

0,65

0,55

0,45

0,7

0,6

0,5

0,4

0 1 2 3 4 5 6

Modes "m"

Xf=0,25 Xf=0,35 Xf=0,50 Xf=0,60 Moyenne

Figure 3.24 : Influence du taux de fibres sur le comportement de la flèche d'une poutre (EE).

44

Chapitre 3 : Simulation numérique du comportement vibratoire d'une structure composite

Plus le taux de fibres est important dans une poutre moins la flèche est importante. Mais, nous observons une modification de la période d'oscillation. Donc, le taux de fibres est responsable de la diminution de la flèche.

Tableau 3.11 : Valeurs des fréquences maximales pour différents taux de fibres d'une poutre EE suivant les 5 premiers modes d'excitations.

Poutre EE	Composite : Polyester/RC
	Fréquence angulaire maximale (Rad/s)
Modes	???? = ??.????	???? = ??.????	???? = ??.????	???? = ??.????
1	115,8	124,8	137,8	146,3
2	463,2	499	551,18	585,3
3	1042,2	1122,8	1240,2	1316,8
4	1852,8	1996,1	2204,8	2341,1
5	2894,9	3118,9	3444,9	3657,9
Moyenne	1273,78	1372,32	1515,776	1609,48
Ecart type	1119,697	1206,327	1332,43	1414,814

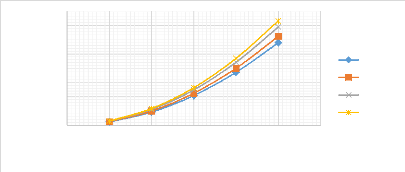
ù0max (rad/s)

4000,4

3500,4

3000,4

2500,4

2000,4

1500,4

1000,4

500,4

0,4

0 1 2 3 4 5 6

Modes "m"

Xf=0,25 Xf=0,35 Xf=0,50 Xf=0,60

Figure 3.25 : Influence du taux de fibres sur les fréquences angulaires dans une poutre (EE)

Les graphes des figures (3.12 et 3.13) montrent que plus le taux de fibres est important dans une poutre (EE), plus la fréquence angulaire est aussi importante.

f) Influence du module d'Young des fibres sur le comportement de la flèche maximale. Dans ce test, il est question de faire varier le taux de fibres d'une poutre et observer le comportement de la flèche.

Tableau 3.12 : Valeurs des flèches maximales pour différents modules d'Young d'une poutre EE suivant les 5 premiers modes d'excitations.

Poutre EE	Composite : Polyester/RC					?? = ??????	???? = ??.????
	Flèche maximale (mm)					?????????? = ??.??	?????????? = ????
Modes	??????????	??/????????	???? = ??????	??/????????	??????????	Moyenne	Ecart type
1	1,0649	0,9946	0,5830	0,445	0,3598	0,68946	0,32165033
2	1,0120	0,9452	0,5540	0,4228	0,3419	0,65518	0,30570179
3	1,0142	0,9473	0,5552	0,4238	0,3426	0,65662	0,30637316
4	1,0141	0,9472	0,5552	0,4237	0,3426	0,65656	0,30633926
5	1,0141	0,9472	0,5552	0,4237	0,3426	0,65656	0,30633926

45

Chapitre 3 : Simulation numérique du comportement vibratoire d'une structure composite

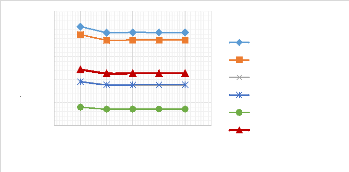
w0max (mm)

0,8

0,6

0,4

0,2

1,2

1

0 1 2 3 4 5 6

Modes "m"

Ef=Efmin=2,3 Ef=1/3Efmoy=2,83 Ef=Efmoy=8,5 Ef=3/2Efmoy=12,75 Ef=Efmax=17 Moyenne

Figure 3.26 : Influence du module d'Young des fibres sur le comportement de la flèche de la poutre (EE). Plus le module d'Young de fibres est important dans une poutre moins la flèche est importante. Donc plus les fibres sont résistantes, plus la structure est rigide et plus la flèche est réduite. Ceci s'accorde avec les résultats obtenus lorsque nous faisions varier la hauteur.

Tableau 3.13 : Valeurs des fréquences maximales pour différents modules d'Young des fibres d'une poutre EE suivant les 5 premiers modes d'excitations.

Poutre EE	Composite : Polyester/RC					a = 150	Xf = 0.35
	Flèche maximale (mm)					Ef = 8.5	Ef = 8.5
Modes	Efmin	1/3Ef m	Ef = Ef m	3/2Efm	Efma	Moyenne	Ecart type
1	92,3	95,5	124,8	142,8	158,8	122,84	29,0496
2	369,2	382,1	499	571,2	635,2	491,34	116,1718
3	830,8	859,6	1122,8	1285,2	1429,3	1105,54	261,4214
4	1479,6	1528,2	1996,1	2284,9	2541	1965,96	464,0802
5	2307,7	2387,8	3118,9	3570,1	3970,3	3070,96	726,2101

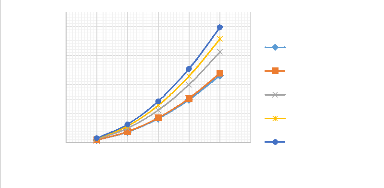
ù0max (rad/s)

2500,4

2000,4

4500,4

4000,4

3500,4

3000,4

1500,4

1000,4

500,4

0,4

0 1 2 3 4 5 6

Modes "m"

Ef=Efmin=2,3 Ef=1/3Efmoy=2,83 Ef=Efmoy=8,5 Ef=3/2Efmoy=12,75 Ef=Efmax=17

Figure 3.27 : Influence du taux de fibres sur les fréquences angulaires dans une poutre (EE)

Les graphes des figures (3.12 et 3.13) montrent que plus le module d'Young des fibres est important dans une poutre (EE), plus la fréquence angulaire est aussi importante. Donc, la fréquence angulaire varie avec la résistance des fibres.

46

Chapitre 3 : Simulation numérique du comportement vibratoire d'une structure composite

3.3.2.2. Cas d'une poutre EL

Dans ce cas, les poutres simulées sont prismatiques de dimensions 150x15x15 mm à section rectangulaire renforcées avec un taux X f = 35%.

a) Variation de la flèche maximale en fonction des dix premiers modes d'excitations Présentation graphique des résultats

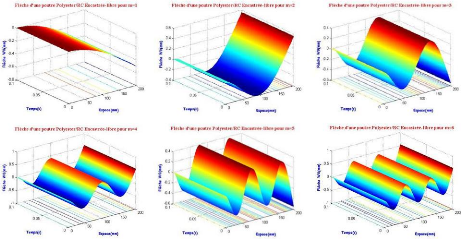
Figure 3.28 : Comportement de la flèche pour les 6 premiers modes d'une poutre EL Présentation numérique des résultats

Ces résultats présentent les valeurs des flèches maximales pour les différents modes. Tableau 3.14 : Valeurs des flèches maximales pour les 10 premiers modes d'une poutre EL

Flèche maximale d'une poutre composite encastrée en Polyester/RC
X f = 35% ; ; ; : rectangulaire ;150x15x15
Modes	1	2	3	4	5	6	7	8	9	10
Flèche (mm)	0,5050	0,5505	0,5506	0,5506	0,5506	0,5506	0,5506	0,5506	0,5506	0,5506

Pour une poutre encastrée-libre, la flèche croit et converge pour les 3 premiers modes et devient constante jusqu'au 10^ème mode.

W0max (mm)

0,56

0,55

0,54

0,53

0,52

0,51

0,5

0 1 2 3 4 5 6

0,505

0,5505 0,5506 0,5506 0,5506

Modes "m"

Flèche (mm)

Figure 3.29 : Graphe de variation de la flèche maximale en fonction des modes

47

Chapitre 3 : Simulation numérique du comportement vibratoire d'une structure composite

Le mode fondamental 1 est le moins influent car, présente la flèche minimale. Le mode 2 traduit le régime transitoire avec un pourcentage d'élévation de 8,2% du mode 1 ; le mode 3 et les autres modes traduisent le régime permanant avec un pourcentage d'élévation de 0,02% par rapport au mode 2 et un écart relatif de 9,03% avec le mode fondamental présenté comme le plus dangereux.

Influence du taux de fibres sur le comportement de la flèche maximale.

Dans ce test, il est question de faire varier le taux de fibres d'une poutre et observer le comportement de la flèche.

Tableau 3.15 : Valeurs des flèches maximales pour différents taux de fibres d'une poutre EL suivant les 5 premiers modes d'excitations.

Poutre EL	Composite : Polyester/RC				a = 150
	Flèche maximale (mm)				Ef = 8.5
Modes	Xf= 0.25	Xf= 0.35	Xf= 0.50	Xf= 0.60	Moyenne mi
1	0,5644	0,5050	0,4377	0,4026	0,477425
2	0,6153	0,5505	0,4771	0,4389	0,52045
3	0,6154	0,5506	0,4472	0,4390	0,52055
4	0,6154	0,5506	0,4472	0,4390	0,52055
5	0,6154	0,5506	0,4472	0,4390	0,52055

w0max (mm)

0,65

0,55

0,45

0,6

0,5

0,4

0 1 2 3 4 5 6

Modes "m"

Xf=0,25 Xf=0,35 Xf=0,50 Xf=0,60 Moyenne

Figure 3.30 : Influence du taux de fibres sur le comportement de la flèche d'une poutre (EL).

Donc, plus le taux de fibres est important dans une poutre EL moins la flèche est importante. Les figures ci-dessus montrent une poutre EL à section rectangulaire de longueur « a=200, h=15, » excitée au mode 5 renforcé avec un taux de fibres > 35%.

48

Chapitre 3 : Simulation numérique du comportement vibratoire d'une structure composite

Figure 3.31 : Influence un taux de fibres > 35% de la poutre (EL) sur les caractéristiques vibratoires.

Figure 3.32 : Influence un taux de fibres < 35% de la poutre (EL) sur les caractéristiques vibratoires. Du point de vue cinématique, la poutre EL a plus de degrés de libertés que la poutre EE. Donc lorsqu'on structure possède moins de degrés de libertés, le mode fondamental n'est plus critique.

3.3.2.3. Cas d'une poutre AA

Dans ce cas, les poutres simulées sont prismatiques de dimensions 150x15x15 mm à section

rectangulaire renforcées avec un taux X?? = 35%. Présentation graphique des résultats

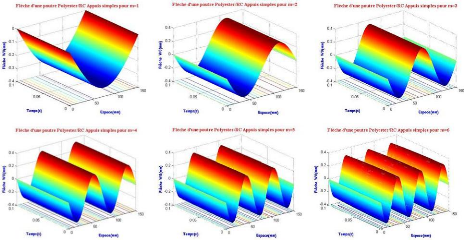
Figure 3.33 : Comportement de la flèche pour les 8 premiers modes d'une poutre AA Présentation numérique des résultats

49

Chapitre 3 : Simulation numérique du comportement vibratoire d'une structure composite

a) Influence de la longueur de la poutre sur le comportement de la flèche maximale. Dans ce test il est question de faire varier la longueur « a » de la poutre, puis visualiser le

comportement de la flèche.

Tableau 3.16 : Valeurs des flèches maximales avec différentes longueurs pour les 5 premiers modes d'une poutre AA.

Poutre AA	Composite : Polyester/RC						Xf = 0.35		Ef = 8.5
	g0 = 1N						h = 15		Longueur
a = 80	a = 150	a = 200	a = 500	a = 750	a = 1000	Moyenne	Ecart type		w0max
0,6883	0,3671	0,275	0,1101	0,0734	0,0551	0,2615	0,242650522

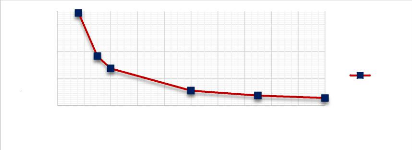
w0max (mm)

0,6

0,4

0,2

0

0 100 200 300 400 500 600 700 800 900 1000

longueur "a" (mm)

w0max

Figure 3.34 : Comportement de la flèche en fonction de la longueur d'une poutre AA Donc la flèche maximale décroit et converge avec la diminution longueur d'une poutre AA.

b) Influence de la hauteur de la poutre sur le comportement de la flèche maximale.

Dans ce test il est question de faire varier la hauteur « h » de la poutre, puis visualiser le comportement de la flèche.

Tableau 3.17: Valeurs des flèches maximales avec différentes longueurs pour les 5 premiers modes d'une poutre AA.

Poutre AA	Composite : Polyester/RC						Xf = 0.35	Ef = 8.5
	Flèche maximale (mm)						g0 = 1N	h = 15
Longueur	h = 8	h = 10	h = 12	h = 15	h = 18	h = 20	Moyenne	Ecart type
w0max	0,3630	0,1858	0,1075	0,0551	0,0319	0,0232	0,12775	0,118686123

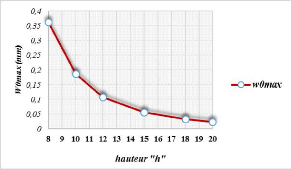
Figure 3.35 : Comportement de la flèche en fonction de la hauteur d'une poutre AA

50

Chapitre 3 : Simulation numérique du comportement vibratoire d'une structure composite

Donc la flèche maximale décroit et converge avec la croissance de la hauteur d'une poutre AA.

c) Influence du taux de fibres sur le comportement de la flèche maximale d'une poutre AA. Dans ce test il est question de faire varier la hauteur « h » de la poutre, puis visualiser le comportement de la flèche.

Tableau 3.18: Valeurs des flèches maximales avec différentes longueurs pour les 5 premiers modes d'une poutre EE.

Poutre AA	Composite : Polyester/RC				Xf = 0.35	Ef = s. 5
	Flèche maximale (mm)				g0 = 1N	h = 15
Longueur	X f = 0.25	Xf = 0.35	Xf = 0.50	Xf = 0.60	Moyenne	Ecart type
w0max	0,0615	0,0551	0,0477	0,0439	0,05205	0,007830496

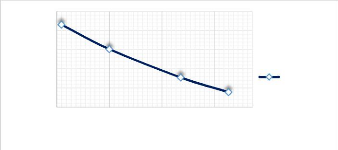
W0max (mm)

0,065

0,055

0,045

0,06

0,05

0,04

0,24 0,35 0,46 0,57

hauteur "Xf"

w0max

Figure 3.36 : Comportement de la flèche en fonction du taux de fibre dans la poutre AA

Donc la flèche maximale décroit et converge avec la croissance du taux de fibre contenu dans une poutre AA.

3.3.2.4. Conclusion simulation des poutres

Donc, pour une application de poutres nécessitant une minimisation de la flèche, il est

recommandé d'après cette analyse d'utiliser une poutre de longueur supérieure à 200 mm, de hauteur supérieure ou égale à 15 mm, avec un taux de fibres supérieur ou égal à 35% de module d'Young moyen supérieur ou égal à 8,5 GPa.

3.3.3. Modélisation des éléments dans le cas d'une plaque en appuis simples Considérons une plaque (pli orthotrope) rectangulaire constituée d'une matrice de polyester et de

fibres de RC. Le pli est unidirectionnel et orienté à 0°.

Mode 1 : m=1 ; n=1 Mode 2 : m=1 ; n=2 Mode 2 : m=2 ; n=1

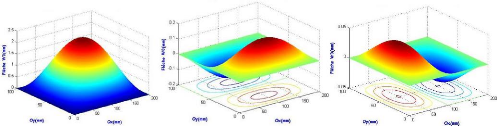
Chapitre 3 : Simulation numérique du comportement vibratoire d'une structure composite

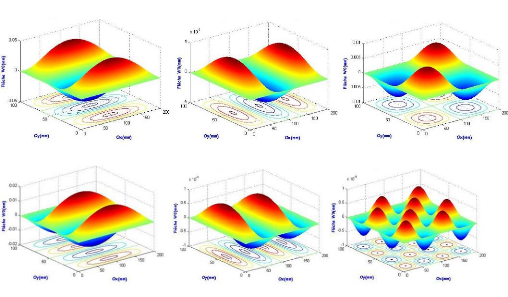
Mode 3 : m=1 ; n=3 Mode 3 : m=3 ; n=1 Mode 3 : m=2 ; n=2

Mode 4 : m=1 ; n=4 Mode 4 : m=4 ; n=1 Mode 4 : m=4 ; n=4

Mode 5 : m=1 ; n=5 Mode 5 : m=5 ; n=1 Mode 5 : m=5 ; n=5

51

Figure 3.37 : Comportement de la flèche d'une plaque AAAA (pli à 0°) pour 5 modes. Présentation numérique des résultats

Ces résultats présentent les valeurs des flèches maximales pour les différents modes. Tableau 3.19 : Valeurs des flèches maximales pour les 5 premiers modes d'une plaque AAAA

Em = 2, 8 GPa		Plaque rectangulaire 200x100x0,35 en composite Polyester/RC						Xf = 0.35
E = 8, 5 GPa								g0 = 100 N
Modes	1	2		3		4		5
m	1	1	2	1	3	1	4	1	5
n	1	2	1	3	1	4	1	5	1
Pli à 0°
W0Ma?? 2,314 0,17 0,042 0,0417 0,0041 0,016 8,33E-5 0,007 2,49E-5
Pli à 90°
W0Ma?? 0,4524 0,0032 0,1060 2,8E-4 0,0343 5,47E-4 0,0145 1,6E-4 0,0073

52

Chapitre 3 : Simulation numérique du comportement vibratoire d'une structure composite

				Stratifié [0/90]5
W0Max	0,032	0,0018	0,0018	4,25E-4 4,25E-4	1,62E-4	1,62E-4	7,87E-5	7,87E-5
				Stratifié [0/90]5
W0Max	0,3991	0,0222	0,0222	0,0053 0,0053	0,0020	0,0020	9,78E-4	9,78E-4

Ces résultats montrent que le mode fondamental est le plus dangereux. Car, la flèche est maximale pour ce mode. Les graphes ci-dessous présentent le comportement de la flèche pour les différentes structures.

1 2 3 4 5

Modes

2,5

2

1,5

1

W0Max

0,5

0

2,314

0,17

0,047 0,016 0,007

w0max pli à 0°

Figure 3.38 : Comportement de la flèche d'une plaque AAAA (pli à 0°) pour 5 modes.

Pour un pli à 0°, la flèche au mode 2 est obtenue avec un pourcentage de chute de 92.65% sur le mode fondamental 1. Cette flèche décroit et converge avec les modes.

W0Max

0,45

0,35

0,25

0,15

0,05

0,5

0,4

0,3

0,2

0,1

0

0,4524

1 2 3 4 5

Modes

0,106

0,0343

0,0145

0,0073

w0max pli à 90°

Figure 3.39 : Comportement de la flèche d'une plaque AAAA (pli à 90°) pour 5 modes.

Pour un pli à 90°, la flèche au mode 2 est obtenue avec un pourcentage de chute de 76.57% sur le mode fondamental 1. Cette flèche décroit et converge avec les modes.

53

Chapitre 3 : Simulation numérique du comportement vibratoire d'une structure composite

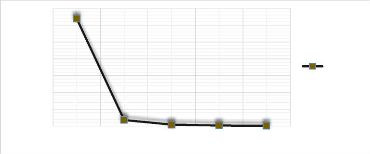
W0Max

0,035

0,025

0,015

0,005

0,03

0,02

0,01

0

0,032

1 2 3 4 5

Modes

0,0018

4,25E-04 1,62E-04

7,87E-05

w0max
stratifié
[0/90]s

Figure 3.40 : Comportement de la flèche d'une plaque AAAA (stratifié symétrique à [0/90]_s) pour 5 modes. Pour un stratifié symétrique à [0/90]_s, la flèche au mode 2 est obtenue avec un pourcentage de chute de 94.375% sur le mode fondamental 1. Cette flèche décroit et converge avec les modes.

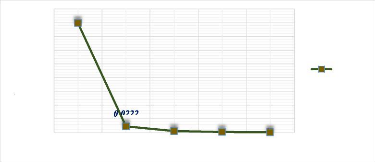
W0Max

0,45

0,35

0,25

0,15

0,05

0,4

0,3

0,2

0,1

0

0,3991

1 2 3 4 5

Modes

0

02
,

0,002 9,78E-04

w0max stratifié...

Figure 3.41 : Comportement de la flèche d'une plaque AAAA (stratifié antisymétrique à [0/90]_s) pour les 5

premiers modes.

Pour un stratifié antisymétrique à [0/90]_s, la flèche au mode 2 est obtenue avec un pourcentage de chute de 94.44% sur le mode fondamental 1. Cette flèche décroit et converge avec les modes.

En définitive, les objectifs que nous poursuivons dans ce chapitre ont été atteint, à savoir visualiser et analyser le comportement des éléments de structures (plaques et poutres). L'implémentation des équations sous Matlab nous a fourni des résultats acceptables, car pour chaque élément testé, les conditions aux limites étaient respectées au préalable. Il a été constaté que les paramètres comme la longueur, la hauteur, le taux de renforcement et le module d'Young des fibres influencent raisonnablement sur le comportement de la flèche au cours des vibrations transversales libres pour une structure sollicitée en flexion et configurée sous diverses conditions aux limites essentiellement. Aussi, nous avons constaté que ces caractéristiques influencent sur la fréquence angulaire propre et la période des oscillations. Les résultats obtenus restent à être valider soit par une confrontation avec des résultats expérimentaux, soit par confrontation avec les résultats de la méthode des éléments finis ou par confrontation des résultats d'un test expérimental tiré de la littérature. Ces deux derniers process de validation seront développés dans le chapitre 4.

CHAPITRE 4 : SIMULATION NUMERIQUE SOUS ABAQUS DU COMPORTEMENT DE LA FLECHE D'UNE STRUCTURE COMPOSITE ET VALIDATION DU CODE DE CALCUL

Chapitre 4 :

SIMULATION NUMERIQUE SOUS ABAQUS DU COMPORTEMENT DE LA FLECHE D'UNE STRUCTURE COMPOSITE ET VALIDATION DU CODE DE CALCUL

La méthode des éléments finis est très utilisée pour résoudre directement des problèmes qui ne sont pas ou sont difficilement résolubles avec les méthodes analytiques. Ce modèle est capable de gérer des séquences d'empilement arbitraires. Ainsi, la méthode des éléments finis donne la possibilité de trouver la solution la plus proche de la réalité, en remplaçant le système continu par un système discret caractérisé par un nombre finis de paramètres. Dans le cadre de ce travail, nous présenterons d'abord la méthode éléments finis, ensuite nous allons modéliser grâce au logiciel Abaqus le comportement de la flèche d'un matériau composite, les résultats obtenus par ce dernier seront confrontés avec ceux obtenus au chapitre 3 et enfin, nous allons procéder à la validation du code de calcul développé à partir d'une confrontation des résultats du code de calcul développé avec ceux obtenus expérimentalement sur une structure stratifiée [0/90] par les travaux de M. Assarar, A. El Mahi & J.-M. Berthelot présentés dans le cadre 19^ème Congrès Français de Mécanique tenu à Marseille, les 24 et 28 août 2009.

Chapitre 4 : Simulation numérique sous Abaqus du comportement de la flèche d'une structure composite et validation du code

55

4.1. Présentation de la méthode des éléments finis

Comme toutes les méthodes, la méthode des éléments finis est basée sur un principe et possède une méthode de résolution des problèmes.

4.1.1. Principe de la méthode des éléments finis

L'analyse du comportement d'une structure par la méthode des éléments finis consiste à mailler ou discrétiser la structure considérée en éléments (segment de droit ou arc pour une structure linéique ; triangle ou quadrilatère pour une structure surfacique ; prisme, tétraèdre, hexaèdre, etc. pour une structure volumique) et à établir aux noeuds du maillage les relations force-déplacement, en tenant comptes des conditions aux limites et de chargement de la structure. Le champ des déplacements en un point quelconque est obtenu par résolution numérique du système d'équations linéaires de grande dimension.

Pour créer le maillage d'une structure, il faut la subdiviser en petits morceaux polygonaux sans créer des recouvrements et des ouvertures. Donc le maillage est un ensemble de sous- domaines fermés de formes géométriques polygonaux.

4.1.2. Différentes étapes de la méthode des éléments finis

Elle possède quatre étapes principales :

(1) Le maillage : c'est la décomposition de la géométrie en sous domaines de formes géométriques simples ;

(2) Champ de déplacement élémentaire : pour un élément e, ressortir l'expression du champ de déplacement en fonction des déplacements aux noeuds (degrés de libertés) de l'élément, ainsi que l'énergie de déformation et la matrice de rigidité ;

(3) Assemblage : à partir des matrices élémentaires respectives, établir les matrices globales (rigidité, masse, force, etc.) par assemblage ;

(4) Conditions et solutions : mettre en place les différentes conditions aux limites et de chargement de la structure puis déterminer les déplacements inconnus, ainsi que les déformations et les contraintes dans chaque élément.

4.2. Modélisation du comportement de la flèche d'un matériau composite en vibrations libres transverses

L'objectif essentiel d'une simulation utilisant les méthodes numériques dans le domaine de génie mécanique réside à prédire correctement le comportement des pièces ou des mécanismes durant leur fabrication et en état de service à partir des caractéristiques mécaniques de chacun des composants du dispositif étudié et de leurs interfaces.

4.2.1. Intérêt de la modélisation numérique

Durant ces dernières années, l'essor du calcul numérique a indubitablement accéléré dans le secteur industriel et il offre des possibilités tels que :

Chapitre 4 : Simulation numérique sous Abaqus du comportement de la flèche d'une structure composite et validation du code

56

? La description complète de la situation analysée : les champs de déplacements, contraintes, fréquentielles sont facilement déterminés par une relation cause-conséquences.

? L'estimation des paramètres difficilement accessibles : le calcul des critères d'endommagement difficilement mesurables au cours des essais et de suivre en continu l'évolution de dégradation du matériau sur l'ensemble de la pièce ;

? La modification, l'amélioration et l'innovation potentielles : possibilité d'effectuer par d'effectuer une analyse du comportement en fonctionnement d'une pièce sans avoir à la fabriquer. Ce qui a pour avantage de modifier, aisément et autant que nécessaire la géométrie, le design, les conditions d'utilisation ainsi que l'ensemble des différents paramètres pouvant avoir une influence sur le comportement des différents éléments concernés ;

? La limitation du coût des études : la modélisation numérique permet de réduire le financement tout en gagnant en temps au cours d'un projet ;

? La réduction des risques industriels : testé préalablement de façon numérique, le comportement des pièces en développement limite fortement les risques de casse et minimise donc les risques d'incidents matériels et humains.

La modélisation numérique présente donc de nombreux avantages par rapport aux expérimentations en laboratoire ou en conditions industrielles. Sa mise en oeuvre nécessite toutefois une bonne connaissance de la réalité industrielle et des phénomènes physiques mis en jeu, ainsi que certains moyens matériels. Par contre, elle ne permet pas de s'affranchir de l'étape finale qu'est la validation expérimentale ou industrielle. Cette validation s'effectuant à partir d'expériences dont les résultats sont plus ou moins dispersés. Les simulations numériques ne permettent d'obtenir qu'une estimation de la réalité.

4.2.2. Justification du choix de ABAQUS

Le choix du code ABAQUS repose principalement sur deux raisons. D'une part, de nombreux travaux de modélisation numérique adaptés aux problèmes spécifiques des vibrations en flexion ont été réalisés avec succès en utilisant ce code. D'autre part, les diverses capacités de ce code correspondent bien à nos besoins, à savoir, ABAQUS permet de prendre en compte les caractéristiques spécifiques des constituants d'un matériau composite (direction des fibres, nombres de couche, épaisseur des couches, et même les différents modules de l'ingénieur peuvent être définies suivant chaque direction, etc.). La puissance d'Abaqus nous permet de choisir le type de composite (orthotrope, unidirectionnel, etc.). Il ouvre notamment une porte aux utilisateurs en leur permettant de programmer des lois de comportement spécifiques des matériaux et des interfaces. Aussi, le maillage du code prend en compte la théorie de Love-Kirchhoff à travers le type d'élément STRI68. Ce code est puissant et comporte des modules utiles, tel que le module en langage Python script afin de faciliter une étude paramétrique sous ABAQUS. Tous

Chapitre 4 : Simulation numérique sous Abaqus du comportement de la flèche d'une structure composite et validation du code

57

ces points forts de ce code nous ont finalement conduit à utiliser ABAQUS pour le développement d'un modèle numérique par éléments finis dans le cadre de cette recherche.

4.2.3. Présentation du composites étudiés

4.2.3.1. Objectif de la modélisation

La modélisation numérique par ABAQUS dans le cadre de ce travail permettra d'une part de faire une comparaison des résultats numériques par éléments finis et ceux obtenus par MATLAB au chapitre 3 et d'autre part de valider les résultats de MATLAB à l'aide d'un modèle d'une comparaison avec les résultats expérimentaux contenu dans la littérature.

4.2.3.2. Constituants des composites étudié

Le composite étudié est identique à celui présenté au §-3.2.

4.2.3.3. Eléments à modéliser

Au cours de l'analyse, nous aurons à étudier des éléments rectangulaires de types poutre et plaque. Tableau 4.20 : Présentation géométrique des éléments à modéliser

	Plaque				Poutre
Illustrations
Caractéristiques Géométriques

4.2.3.4. Les conditions aux limites à étudier

Les différentes conditions aux limites à imposer aux éléments sont :

? Plaque en appuis simples ; ? Poutre en appuis simples ; ? Poutre encastrée-libre.

4.3. Modélisation par éléments finis avec ABAQUS du comportement de la flèche d'un matériau composite en vibrations libres transverses

4.3.1. Présentation du logiciel ABAQUS

Comme tous les logiciels d'éléments finis, la résolution d'un problème de mécanique dans ABAQUS se fait par une succession d'étapes faisant intervenir plusieurs modules. Les différents modules sont :

- Le module Part : module servant à définir la géométrie des entités du modèle. Ces entités comprennent parfois des parties déformables et des parties rigides. Son icône est :

Chapitre 4 : Simulation numérique sous Abaqus du comportement de la flèche d'une structure composite et validation du code

58

- Le module Property : il permet de définir les propriétés du matériau (des parties déformables) et la masse des corps rigides si nécessaire. Pour créer un matériau, il suffit de cliquer sur l'icône :

Ensuite, il faut créer une section afin d'y affecter les propriétés du matériau à une entité du maillage (a) et enfin, il faut affecter la section créée à l'entité crée dans le module Part (b). Cela se fait au moyen des icônes :

(a) (b)

- Le module Assembly : il s'agit de créer une (voire plusieurs) instance(s) à partir des entités que vous avez définies dans le module Part. Ces instances seront celles que vous manipulerez par la suite dans le modèle. Il est accessible par le bouton :

- Le module Step : il permet de définir le type d'étude (statique, dynamique, etc.). Il est accessible à partir du bouton :

- Le module Interaction : il permet de définir les interactions entre différentes entités du modèle,

ce qui peut prendre la forme d'un contact ou d'équations de liaison entre degrés de liberté.

- Le module Load : il permet de définir les différentes conditions d'étude comme : le chargement (a), les conditions aux limites (b) et les vitesses (c).

(a) (b) (c)

- Le module Mesh : il permet de définir les caractéristiques du maillage comme : le pas et le type d'éléments(a) d'une part et d'exécuter le maillage (b) d'autre part. ceci est exécutable par les icônes :

(a) (b)

- Le module Job : il permet le « lancement » du calcul. Après avoir lancé le calcul, vous pouvez suivre l'évolution du process en cliquant sur « Monitor » : vous pouvez ainsi avoir en temps réel l'évolution des incréments de chargement et apprécier la convergence des calculs.

Chapitre 4 : Simulation numérique sous Abaqus du comportement de la flèche d'une structure composite et validation du code

4.3.2. Comportement de la flèche des plaques par la méthode des éléments finis et comparaison avec les résultats du code développé.

4.3.2.1. Conditions aux limites : plaque en appuis simples sur ses quatre côtés

Nombre d'élément de base : ; Types d'éléments : STRI68⁶
4.3.2.1.1. Résultats

? Présentation graphique des résultats

Mode1 : ; Mode 2 : ; ;

W _{0 C} ( _Max )

W _{0 A} ( _Max )

E w 0(max) ? w _{0 A} ( _Max ) ? w _{0 C} ( _Max )

59

Mode 3 : ; ; Mode 4 : ; ;

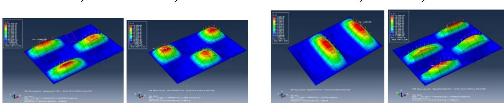
Figure 4.42: Présentation graphique du comportement de la flèche sur un pli orthotrope ? Présentation numérique des résultats

Le tableau ci-dessous, répertorie les différentes valeurs des flèches maximales extraites dans le calcul par éléments finis à l'aide de ABAQUS. Aussi, ces résultats sont confrontés par ceux du code de calcul dans le but de mettre en vue l'erreur relative qui existe entre les deux méthodes.

Tableau 4.21 : Comparaison des résultats obtenus par ABAQUS avec ceux du code développé.

_w ? _w

_{0 A} ( _Max ) _{0 C} ( _Max )

? ₁₀₀

? _x
w _{0 A} ( _Max )

	; ;
Modes	m	n	CODE (mm)	ABAQUS (mm)	Ecart (mm)	Ecart relatif i (%)
			AAAA	AAAA
1	1	1	1.00060	1.06081	0.06021	5.67
2	1	2	1.00600	1.04100	0.035	3.36
	2	1	1.00600	1.04100	0.035	3.36
3	2	3	1.00000	1.03208	0.03208	3.11
	3	2	1.00000	1.03208	0.03208	3.11
4	1	4	1.00000	1.00000	0.000	0.00

6 STRI68 désigne le type d'élément répondant aux hypothèses de Love-Kirchhoff

Chapitre 4 : Simulation numérique sous Abaqus du comportement de la flèche d'une structure composite et validation du code

60

	4	1	1.00000	1.00000	0.000	0.00
5	1	5	1.00000	1.00000	0.000	0.00
	5	1	1.00000	1.00000	0.000	0.00

Le graphe ci-dessous rend plus visible l'écart relatif entre les deux résultats.

0 1 2 3 4 5 6

Modes

1,07

1,01

0,99

ABAQUS MATLAB

1,05

W0max

1,03

1,06081

1,041

1,03208

1,006

1,0006

Figure 4.43 : Présentation graphique de l'écart relatif entre la flèche maximale calculée par
MATLAB et celle calculée par ABAQUS.

Cette représentation graphique nous montre dans le sens vertical la dispersion des deux courbes. Cette dispersion est considérable pour les trois premiers modes d'excitations.

4.3.2.1.2. Explication du phénomène de dispersion

Le phénomène de dispersion peut être lié à une erreur du code de calcul développé ou une erreur

de configuration des paramètres de maillage de la structure. Cette dernière nous poussera à analyser l'influence du nombre d'éléments (pas) sur le comportement de la flèche d'une plaque.

4.3.2.1.3. Influence du nombre d'éléments

Pour la même plaque, nous reprenons le test sous ABAQUS en faisant varier le nombre d'éléments.

Tableau 4.22 : Comportement de la flèche d'une plaque AAAA en fonction du nombre d'éléments.

Modes	m	n	W0max ABAQUS (mm)						W0max MATLAB (mm)
			5 éléments	20 éléments	30 éléments	80 éléments	100 éléments	1000 éléments
1	1	1	1.05092	1.13572	1.06081	1.00660	1.00010	1.000001	1.00060
2	1	2	1.14216	1.13804	1.04100	1.00440	1.00001	1.00000	1.00600
	2	1	1.14216	1.13804	1.04100	1.00440	1.00001	1.00000	1.00600
3	2	3	1.13572	1.13572	1.03208	1.00208	1.00000	1.00000	1.00000
	3	2	1.13572	1.13572	1.03208	1.00208	1.00000	1.00000	1.00000
4	1	4	1.13572	1.12100	1.00000	1.00000	1.00000	1.00000	1.00000
	4	1	1.13572	1.12100	1.00000	1.00000	1.00000	1.00000	1.00000

Chapitre 4 : Simulation numérique sous Abaqus du comportement de la flèche d'une structure composite et validation du code

61

5

	1	5	1.13572	1.12100	1.00000	1.00000	1.00000	1.00000	1.00000
	5	1	1.13572	1.12100	1.00000	1.00000	1.00000	1.00000	1.00000

L'influence du type d'élément sur le comportement de la flèche est explicitée par le graphe ci-dessous.

W0max

_m ? _{2 n} ? ₃

0,99

1,15

1,13

1,11

1,09

1,07

1,05

1,03

1,01

0 1 2 3 4 5 6

Modes

5 élts

20 élts 30 élts 80 élts 100 élts 1000 élts

W0max MATLAB

Figure 4.44 : Influence du nombre d'éléments sur le comportement de la flèche d'une plaque en appuis simples.

Effectivement, l'influence du nombre d'éléments est considérable sur le comportement de la flèche. Donc, les résultats deviennent acceptables à partir de 100 éléments comparativement au code de calcul développé.

? Présentation graphique des résultats pour un maillage de 100 éléments

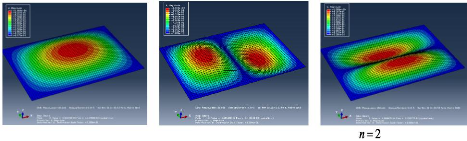
Mode 3 : ; ;

Mode 1 : ; Mode 2 : ; ;

Chapitre 4 : Simulation numérique sous Abaqus du comportement de la flèche d'une structure composite et validation du code

62

Figure 4.45 : Présentation graphique du comportement de la flèche sur une plaque en appuis
simples sur ses 4 extrémités.

4.3.2.2. Conditions aux limites : poutre encastrée à une extrémité et libre sur l'autre.

Nombre d'élément de base : ; Types d'éléments : STRI68

4.3.2.2.1. Résultats

? Présentation graphique des résultats

Mode1 : Mode 2 : Mode 3 :

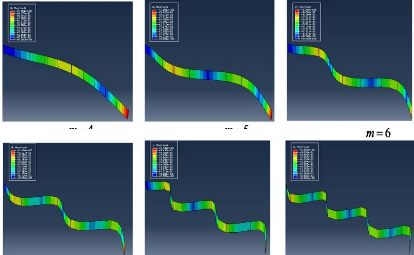
Mode 4 : Mode 5 : Mode 5 :

Figure 4.46 : Présentation graphique du comportement de la flèche sur une poutre EL

? Présentation numérique des résultats

Le tableau ci-dessous, établie la confrontation des résultats des flèches maximales obtenus au

cours du calcul par éléments finis à l'aide de ABAQUS avec ceux du code développé dans Matlab. Le but est de valider le code développé dans Matlab au moyen de l'erreur relative qui existe entre les deux méthodes.

Chapitre 4 : Simulation numérique sous Abaqus du comportement de la flèche d'une structure composite et validation du code

63

Tableau 4.23 : Comparaison des résultats obtenus par ABAQUS avec ceux du code développé.

	; ;
Modes	m	n	CODE (mm)	ABAQUS (mm)	Ecart (mm)	Ecart relatif i (%)
			EL	EL
1	1	1	1.5201	1.50153	-0.01857	-0.012
2	1	2	2.0369	1.99519	-0.04171	-0.021
	2	1	1.9984	1.84315	-0.155225	-0.084
3	2	3	2.0001	1.96815	-0.03195	-0.016
	3	2	2.0000	1.96009	-0.03991	-0.020
4	1	4	2.0000	1.96009	-0.03991	-0.020
	4	1	2.0000	1.96009	-0.03991	-0.020
5	1	5	2.0000	1.96009	-0.03991	-0.020
	5	1	2.0000	1.96009	-0.03991	-0.020

Le graphe ci-dessous rend plus visible l'écart relatif entre les deux résultats.

_ne ? ₃₀

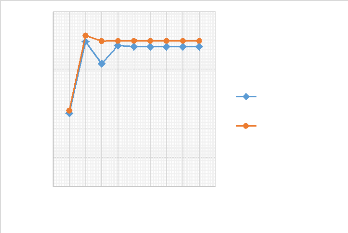
W0max (mm)

2,2

1,8

1,6

1,4

1,2

2

1

0 1 2 3 4 5 6 7 8 9 10 Mode "m"

W0max ABAQUS (mm)

W0max CODE (mm)

_m ? ₁

Figure 4.47 : Présentation graphique du comportement de la flèche sur un pli orthotrope en appuis
simples sur ses 4 extrémités.

Cette représentation graphique nous montre dans le sens vertical la dispersion des deux

courbes. Cette dispersion est considérable entre le mode 2 et 3. La dispersion importante au mode

3 soit un écart relatif de 0,084.

4.3.2.2.2. Conditions aux limites : poutre en appuis simples sur ses deux extrémités.

Nombre d'élément de base : ; Types d'éléments : STRI68

4.3.2.2.3. Résultats

? Présentation graphique des résultats

Mode1 : Mode 2 : Mode 3 :

64

Chapitre 4 : Simulation numérique sous Abaqus du comportement de la flèche d'une structure composite et validation du code

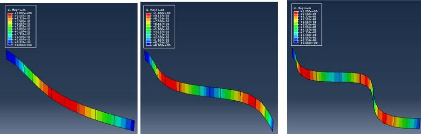
Mode 4 : Mode 5 : Mode 5 :

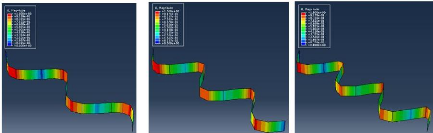
Figure 4.48 : Présentation graphique du comportement de la flèche sur une poutre EL 4.4. Validation du code de calcul

Les études faites au chapitre 2 montrent que la flèche est exprimée en fonction de la fréquence angulaire et du temps. Pour valider le code de calcul développé, il nous suffit de :

· Considérer les travaux de M. Assarar, A. El Mahi & J.-M. Berthelot ;

· Considérer les résultats des fréquences obtenus expérimentalement dans ces travaux ;

_h ? _{15 mm a} ? _{560 mm}

· Entrer les caractéristiques du même composite dans le code de calcul développé dans le cadre de cette recherche ;

· Extraire les résultats des fréquences ;

· Comparer les deux résultats ;

· Commenter la comparaison puis valider le code de calcul.

4.4.1. Présentation des travaux de M. Assarar, A. El Mahi & J.-M. Berthelot [13]

4.4.2. Mise en situation des travaux

Les travaux de M. Assarar, A. El Mahi & J.-M. Berthelot porte sur le thème « Analyse de la réponse dynamique des structures en matériaux composites. » dans le cadre du 19^ème Congrès Français de Mécanique tenu à Marseille, les 24 et 28 août 2009.

4.4.2.1. Présentation du composite et description de l'étude

Le composite est une structure stratifié bidirectionnel du type renforcé par des

fibres de verre, d'épaisseur et de longueur .

65

Chapitre 4 : Simulation numérique sous Abaqus du comportement de la flèche d'une structure composite et validation du code

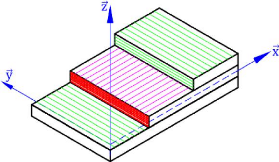
Figure 4.49 : stratifié croisé symétrique considéré pour l'étude

L'étude expérimentale a été menée sur des structures encastrées suivant une section carrée

de . La structure a été excitées en un point proche de l'encastrement à l'aide d'un

marteau d'impact tel que le montre la figure ci-dessous. La réponse a été relevées suivants plusieurs points de manière à détecter tous les modes de vibrations situés dans la bande passante [0, 100 Hz].

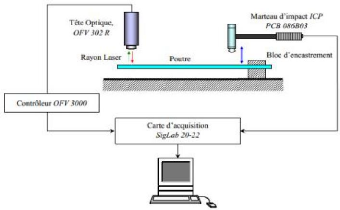
Figure 4.50: Dispositif expérimental utilisé [13].

4.4.2.2. Résultats de l'étude

Les résultats obtenus dans cette recherche sont repertoriés dans le tableau ci-dessous.

Tableau 4.24: Résultats des fréquences calculées par les travaux expérimentaux de M. Assarar, A. El Mahi & J.-M. Berthelot.

Modes	1	2	3	4	5	6	7	8	9		10	Fréquences
											Assarar (Hz)
107	153	215	341	345	457	471	475	538	556

4.4.3. Calcul des fréquences avec le code de calcul

En reportant les caractéristiques de cette structure stratifiée dans le code de calcul développé nous obtenons les résultats du tableau ci-dessous.

66

Chapitre 4 : Simulation numérique sous Abaqus du comportement de la flèche d'une structure composite et validation du code

Tableau 4.25: Résultats des fréquences calculées par le code développé

Modes	1	2	3	4	5	6	7	8	9		10	Fréquences
105.46	150.12	213.24	339.26	343.32	455.64	469.95	473.15	536.41	554.38		MATLAB (Hz)

4.4.4. Comparaison des deux résultats

La comparaison est présentée dans un tableau et une figure. Cette comparaison se fait à partir de l'écart des fréquences obtenu en faisant la différence entre la fréquence des travaux et la fréquence du code. Elle est aussi établie par l'écart relatif dont l'expression est explicitée dans le tableau.

Tableau de comparaison

Tableau 4.26 : Comparaison des fréquences propres calculées par le code de calcul développé avec celles obtenues par des travaux expérimentaux de M. Assarar, A. El Mahi & J.-M. Berthelot.

a = 150 mm ; b = 560 mm et h= 150 mm						Modes
Fréquences Fréquences Matlab (Hz) Assarar (Hz)		Stratifié ELE.f=fTR^-fABAQUsA=fx100 [0/90]STR		Ecart (HZ)fTR-fAaAQUs Ecart relatif 0 (%)
					1
105.46		107	1.57	0.0144	2
150.12		153	2.88	0.0188	3
213.24		215	1.76	0.0082	4
339.26		341	1.74	0.0051	5
343.32		345	1.68	0.0048	6
455.64		457	1.36	0.0029	7
469.95		471	1.05	0.0022	8
473.15		475	1.85	0.0038	9
536.41		538	1.59	0.0029	10
554.38		556	1.62	0.0011

Graphe de comparaison

Le graphe de comparaison présente les courbes des fréquences propres obtenues par les deux résultats en fonction des modes d'excitation.

f (Hz)

200

500

400

300

600

100

0

0 1 2 3 4 5 6 7 8 9 10 11

Mode "m"

Fréquences Matlab (Hz)

Fréquences Assarar (Hz)

Figure 4.51: Dispositif expérimental utilisé.

67

Chapitre 4 : Simulation numérique sous Abaqus du comportement de la flèche d'une structure composite et validation du code

Ecart relatif moyen

Au terme de ce chapitre, force est de constater que l'objectif poursuivi était de confronter les résultats du code de calcul développé au chapitre 3 par des résultats obtenus grâce à un logiciel intégrant les éléments finis et à partir des résultats tirés de la littérature. Cette comparaison, met en exergue une petite erreur de calculs entre les deux résultats. Il est donc clair que les résultats générés dans le code de calcul sont correct avec un écart relatif moyen de 0.6%. En effet, les travaux expérimentaux de M. Assarar, A. El Mahi & J.-M. Berthelot avaient pour objectif de montrer que dans le cas d'une étude dynamique l'on peut s'affranchir d'une analyse expérimentale plus longue et difficile à mettre en place.

CHAPITRE 5 : MISE EN PLACE D'UN LOGICIEL DE CALCUL DE LA FLECHE D'UN COMPOSITE ORTHOTROPE ET CAS PRATIQUE

Chapitre 5 :

MISE EN PLACE D'UN LOGICIEL DE CALCUL DE LA FLECHE D'UN COMPOSITE ORTHOTROPE ET CAS PRATIQUE

De nos jours, l'informatique ou « l'autoroute de l'information » est devenu un moyen de communication efficace et instantané dans le monde. L'information se fait traiter et véhiculer au moyen des logiciels développés selon le besoin. Seulement, la mise sur pieds d'un logiciel est une tâche complexe qui nécessite un maximum de dextérité, car, le développeur doit répertorier l'ensemble des fonctions principales et contraintes du logiciel. Dans le cadre de ce travail, nous mettons sur pieds un outil informatique simple par sa configuration et son utilisation destiné à effectuer une étude de comportement de la flèche des matériaux composites soumis aux vibrations transverses et répondant aux considérations de la flexion. Pour ce faire, nous allons d'abord procéder au choix de l'outil de développement, ensuite définir les attributs du logiciel et enfin écrire le code du logiciel. Par ailleurs, nous effectuerons dans ce même chapitre, une application visant à optimiser la poutre support d'un panneau de signalisation et le logiciel développé nous permettra d'effectuer les différents calculs.

Chapitre 5 : Mise en place d'un logiciel de calcul de la flèche d'un composite orthotrope et cas pratique

5.1. Mise en place d'un logiciel de calcul de la flèche d'un composite

5.1.1. Objectif de la conception du logiciel

En complément de l'introduction, l'objectif de cette conception est d'implémenter le code de calcul développé au chapitre 2 et validé aux chapitres 5 et 6 dans une interface graphique.

5.1.2. Choix de l'outils de développement

Le processus de conception des logiciels étant très complexes, il est nécessaire de choisir un outil de développement puissant, efficace, flexible et simple à manipuler. Parmi la moultitude d'outils de développement comme Scilab, Matlab et Labview nous retiendrons Matlab. En pratique, sous Matlab, toutes les actions doivent être intégralement programmées dans le fichier « M-file ⁷». Ceci offre au programmeur une flexibilité et une liberté au cours du paramétrage de l'interface graphique.

5.1.3. Présentation des attributs du logiciel

Nom, fonction principale et processus de calcul de logiciel constituent les attributs du

logiciel.

5.1.3.1. Nom du logiciel

Le sigle représente le nom du logiciel développé dans le cadre de cette recherche.

En effet, signifie : ; ; ; .
5.1.3.2. Architecture du logiciel

L'architecture donne le processus d'exécution des tâches que doivent mener le logiciel. Aussi les utilisateurs doivent le respecter pour effectuer une analyse du comportement de la flèche.

69

7 Extension du fichier script de Matlab

70

Chapitre 5 : Mise en place d'un logiciel de calcul de la flèche d'un composite orthotrope et cas pratique

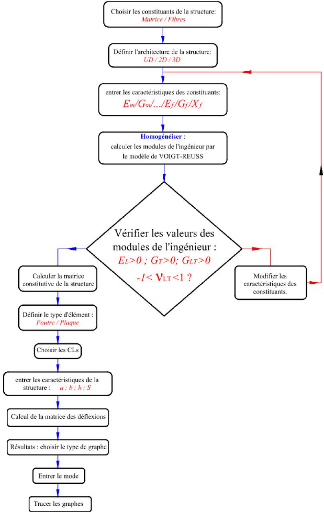
Figure 4.52 : Différentes étapes à suivre pour analyser le comportement de la flèche 5.1.3.3. ` Fonction principale du logiciel

Le logiciel développé sur 3664 lignes de code doit permettre à son utilisateur d'effectuer simplement les études de comportement d'un matériau composite soumis à des vibrations libres, sollicité au flambement et en flexion.

71

Chapitre 5 : Mise en place d'un logiciel de calcul de la flèche d'un composite orthotrope et cas pratique

A cette fonction principale, il en ressort des fonctions contraintes suivantes :

· Offrir une variété des éléments constitutifs du composite ;

· Entrer les caractéristiques intrinsèques des constituants ;

· Assembler ou homogénéiser un matériau composite par la méthode basée sur les modèles à « bornes » de VOIGT et REUSS ;

· Calcul des différents modules de l'ingénieur (EL, ET, etc.) ;

· Calcul de la matrice constitutive de la structure ;

· Vérification et validation des différents modules de l'ingénieur ;

· Entrer les caractéristiques géométriques et calculer les caractéristiques mécaniques ;

· Définir les conditions aux limites de la structure ;

· Afficher les résultats (graphes de comportement de la flèche et valeur de la flèche maximale) ;

· Générer le rapport sur une feuille de calcul.

5.1.4. Petit tutoriel de

(1) Démarrage et écran d'accueil du logiciel i-VAC

Cliquer sur i-VAC.exe pour lancer l'application. Voici l'écran de démarrage et l'interface d'accueil du logiciel :

Figure 4.53 : Aperçu de l'écran de démarrage et d'accueil du logiciel i-VAC. Cliquer sur le « logo » pour lancer une étude par l'onglet « MATERIAU »

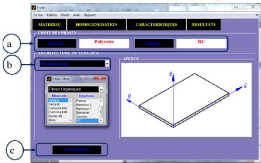
(2) Onglet MATERIAU

(a) Choisir les constituants du composite ;

(b) Choisir le type de structure ;

(c) Cliquer sur « continuer » pour passer à l'onglet « CARACTERISTIQUES ».

Figure 4.54 : Aperçu de l'interface de l'ongle MATERIAU du logiciel i-VAC

(3) Onglet HOMOGENEISATION

Chapitre 5 : Mise en place d'un logiciel de calcul de la flèche d'un composite orthotrope et cas pratique

(a) Entrer les caractéristiques intrinsèques des constituants du composite, puis cliquer sur « homogénéisation » ; (b) Confirmer le nombre de couche, puis cliquer sur « calculer » pour afficher les valeurs des coefficients de rigidité ; (c) Cliquer sur « continuer » pour passer à l'onglet « CARACTERISTIQUES »
	Figure 4.55 : Aperçu de de l'interface de l'ongle

(4) Onglet CARACTERISTIQUES HOMOGENEISATION du logiciel i-VAC

(a) Choisir « Poutre » comme « élément de la structure » ;

(b) choisir « Rectangulaire » comme « type de section » puis remplir les valeurs en respectant les côtes visibles dans la fenêtre aperçu ;

(c)

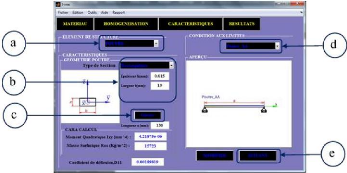
Cliquer sur « Générer » pour effectuer et afficher les résultats de l'étude ;

(d) Choisir les conditions aux limites, pour notre étude prendre « Poutre_AA » ;

(e) Cliquer sur « Suivant » pour

passer à l'onglet

« RESULTATS »

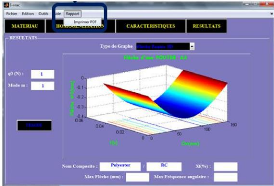
(5) Onglet RESULTATS

Figure 4.57 : Aperçu de de l'interface de l'ongle RESULTATS du logiciel i-VAC.

Figure 4.56 : Aperçu de de l'interface de l'ongle CARACTERISTIQUES du logiciel i-VAC

(a)

72

Choisir le type de graphe ;

(b) Entrer les valeurs q0 en Newtown et le rang du mode que vous souhaitez visualiser ;

(c) Cliquer sur le bouton « TRACER » pour afficher le graphe d'étude ;

(d) Impression du rapport : Menu Rapport >> cliquer sur imprimer rapport ceci imprimera sur format .pdf votre feuille de calcul.

Chapitre 5 : Mise en place d'un logiciel de calcul de la flèche d'un composite orthotrope et cas pratique

5.2. Cas pratique : optimisation du support d'un panneau de signalisation

5.2.1. Mise en situation

Un panneau de signalisation routière est un dispositif sur lequel est marqué un ou plusieurs éléments du signal routier. Fixé sur un support qui est lui-même planter dans le sol dans un massif de fondation, le panneau de signalisation est placé sur le côté de la route et permet de :

? Rendre plus sûre la circulation routière en alertant les usagers des éventuels obstacles qu'ils peuvent rencontrer ;

? Faciliter la circulation en indiquant les directions à suivre ;

? Respecter ou indiquer les différentes prescriptions particulières de police ;

? Donner des indications relatives à l'usage de la route.

Figure 4.58 : Images de différents panneaux de signalisation. [23]

5.2.2. Problématique de l'optimisation

Les supports des panneaux de signalisation routière sont généralement en matériau homogène comme l'acier galvanisé et l'aluminium dont l'extraction du minerai est encore un mystère pour l'industrie camerounaise, de plus, ces matériaux rendent le dispositif lourd. D'où la nécessité de mener une étude sur l'optimisation de ces matériaux homogènes par un matériau local en particulier ceux développés par les différents laboratoires de recherches de l'ENSET de Douala. Cette étude vient surtout mettre en application le code de calcul développé dans le cadre de cette recherche.

Pour le concepteur, le support doit assurer la tenue aux sollicitations mécaniques et climatiques. Ainsi, il doit pouvoir résister aux différentes forces exercées par les vents soufflant sur le site de l'implantation, afin de ne pas se déformer et de ne pas s'arracher ou rompre.

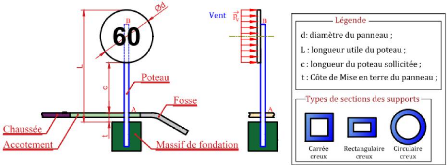
Figure 5.59 : Schéma annoté d'un panneau de signalisation routière

73

Chapitre 5 : Mise en place d'un logiciel de calcul de la flèche d'un composite orthotrope et cas pratique

5.2.3. Objectif de l'optimisation

L'objectif de cette étude est de montrer que les matériaux développés aux différents laboratoires

du Génie Mécanique peuvent s'intégrer dans la conception et la fabrication des supports des panneaux

de signalisation routière. Le paramètre à évaluer pour définir le type de support est le moment fléchissant

(voir Annexe 6) dû à l'effort du vent, pour cela, nous allons :

- Isoler le système (poteau-massif) ;

- Faire le bilan des actions mécaniques appliquées à ce système ;

- Calculer le moment de flexion maximale et déterminer le support normaliser

correspondant ;

_Qv . _z - Evaluer la flèche du système.

_pv . _z

Du point de vue mécanique, la force exercées par le vent engendre des vibrations puis sollicitent

en flexion et en torsion le support.

5.2.4. Etude vibratoire du système

5.2.4.1. Hypothèses de l'étude et données

Dans cette étude, nous admettons que :

? La côte de mise en terre est de 20 Cm ;

? La pression dynamique de base est prise à 130 daN/m² ;

? Pour nos applications numériques nous prendrons : , ; ;

? Les surfaces réelles des panneaux sont prises en compte : ;

? Le moment de torsion est négligé.

Considérons le système ci-contre représentant le support d'un panneau de signalisation pour limitation de vitesse, de gamme normale implanté dans la ville de Douala. Le problème est assimilable à celui d'une poutre encastrée à une extrémité et libre sur l'autre. Cette étude ne traite que l'aspect mécanique du problème, toutefois nous ne mentionnons pas les traitements qu'il faut faire subir à la pièce pour qu'elle résiste mieux aux conditions climatiques et au contact avec le massif de fondation.

5.2.4.2. Bilan des actions mécaniques exercées sur le système

Le problème étant celui d'une poutre encastrée-libre soumise à une force résultante

( sur son extrémité libre) de la pression dynamique sur le panneau de signalisation.
Le système est soumis à :

? ou : la force ou la pression dynamique due au vent ;

_{x x} ? ? _{a 0}

_{w (0)} ? _{0 w '(0)} ? ₀

_w ''( _a ) ? _{0 w} '''( _a ) ? ₀

_Q . _z ? p v

74

_MA

? : le moment d'encastrement en A.

Les conditions aux limites satisfont les équations :

- En A, : et (5.1)

- En B, : , et .

(5.2)

=

_m

Avec :

(5.12)

75

Chapitre 5 : Mise en place d'un logiciel de calcul de la flèche d'un composite orthotrope et cas pratique

, _y , , _y ,

? 0

5.2.4.3. Champ de déplacement cinématiquement admissible du système La plaque étant sollicitée en flexion plane simple, il vient :

(5.3)

5.2.4.4. Expression du moment fléchissant

En effectuant une coupe fictive comme présentée à la figure 5.53, nous avons l'équation d'équilibre statique suivante :

(5.4)

Or : (5.5)

D'où : (5.6)

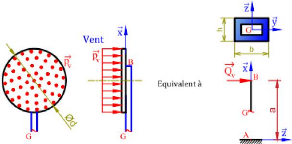
Figure 5.60 : Schéma annoté d'un panneau de signalisation routière Application à un panneau circulaire Nous avons :

(5.7)

AN : (5.8)

(5.9)

Choix de la section : d'après le tableau en annexe 5, la section encastrée correspond à la section critique

et la valeur trouvée nous permet de choisir une poutre à section rectangulaire type SD1, de

_{w x t} ? ? _D ? _t ? _x

₀₍ , ) m cos _m m ( )

. Cette poutre est réalisée sur nos route en acier galvanisé.

5.2.4.5. Flèche maximale du système

? Pour le matériau homogène isotrope en acier galvanisé

Pour un matériau homogène isotrope, le comportement élastique est décrit par le module

d'Young et le coefficient de Poisson .

_Ph

¹¹ ₁₂₍₁ )

? _v

Le coefficient de la matrice de rigidité en flexion est :

(5.10)

( )2 2
_m - _0.5 ?

Les résultats obtenus §2.2.3 deviennent : (5.11)

_m

76

Chapitre 5 : Mise en place d'un logiciel de calcul de la flèche d'un composite orthotrope et cas pratique

Le matériau considéré a pour caractéristiques : ; et

? Pour le composite polyester/RC

Les résultats seront obtenus en introduisant les valeurs correspondantes dans le logiciel i-VAC. A cet effet, nous avons un composite polyester/RC avec un taux de fibres de 35% de module d'Young

de .

5.2.4.6. Présentation et comparaison avec la flèche maximale

Modes		1	2	3	4	5	6
Polyester/RC		4,0731	4,4403	4,4410	4,4410	4,4410	4,4410
		1,1828	4,7313	10,6455	18,9253	29,5708	42,5819
Acier galvanisé		4,0145	4,3763	4,3771	4,3771	4,3771	4,3771
		228,96	915,48	2,06e+3	3,66e+3	5,72e+3	8,24e+3
Ecart relatif :		1,4387	1,4413	1,4388	1,4388	1,4388	1,4388

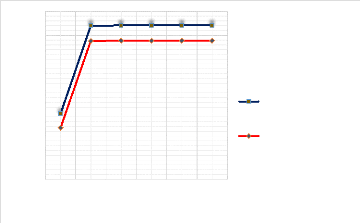
W0Max

4,5

4,4

4,3

4,2

4,1

3,9

3,8

4

1 2 3 4 5 6

Modes

W0comp (.10E-15 mm)

W0acier (.10E-15 mm)

Le support type SD1 en acier galvanisé nous donne une flèche de 4,0145.10^-15 mm au mode fondamental, et la même étude effectuée sur un composite polyester/RC renforcé à 35% de fibres, de

module d'Young de nous donne une flèche de 4,0731.10^-15 mm au même mode soit un écart

relatif de 1,4387%. Donc ce matériau composite est capable de substituer l'acier galvanisé en offrant un plus, la légèreté lors de sa mise en place et le caractère biodégradable.

Parvenu au terme de ce chapitre dont l'objectif était de mettre sur pieds un logiciel d'étude du comportement de la flèche des matériaux composites et sous diverses conditions limites force est de constater que le logiciel fonctionne normalement. Pour y parvenir nous avons écrit 3664 lignes de code dans le logiciel Matlab. Aussi, un cas pratique a été étudié afin de montrer la portée scientifique de ce thème.

77

CONCLUSION GENERALE : BILAN ET PERSPECTIVES

La thématique abordée dans ces travaux est l'étude du comportement de la flèche d'un matériau composite en vibration et simulation sous Matlab. La revue bibliographique présentée au chapitre 1, a montrée que les travaux en vibration des composites sont basés sur la théorie classique des stratifiés et la flèche est l'un des paramètres des équations qui en découlent mais, dépend du type de sollicitation et du type de structure. Ceci nous a permis de restreindre notre étude sur les structures de types Love-Kirchhoff et Euler-Bernoulli considérées comme des plis unidirectionnels ou orthotropes de 0° et 90°, ou stratifié croisé symétrique d'une part et antisymétrique d'autre part. Ainsi, l'objectif visé a été de formuler l'équation de comportement de la flèche de telles structures et d'effectuer une simulation numérique sous Matlab. Les travaux menés pour atteindre cet objectif de recherche ont été développés principalement autour de trois chapitres traités au moyen des considérations posées au chapitre 1. Au chapitre 2, l'équation de comportement de la flèche est obtenue en résolvant par la méthode de séparation des variables et la méthode de Rayleigh-Ritz l'équation différentielle de mouvement transversal d'une structure stratifiée en l'absence des charges transverses à un instant t quelconque. La flèche obtenue dépend des caractéristiques mécaniques d'un matériau, de la fréquence angulaire, du temps et des conditions aux limites. Face à cette dépendance, le logiciel Matlab au chapitre 3 nous a permis de visualiser et de quantifier la valeur maximale de la flèche en prenant un composite à matrice polyester renforcé par des fibres de RC. Au chapitre 4, les résultats développés par le code de calcul s'accordent aux résultats de Abaqus avec un écart relatif moyen de 0,026625%. Ces mêmes résultats, s'accordent avec un écart relatif moyen de 0,06% aux résultats de la littérature provenant des travaux sur une structure stratifiée [0/90]s.

Il était aussi question dans ce même travail de valoriser les produits locaux en intégrant les matériaux composites développés au Laboratoire de Mécanique et Productique de l'UFD dans la loi de comportement de la flèche. A cet effet, nous espérons que ce travail, permettra de retirer une des épines dans le domaine des vibrations des composites. Cependant, les travaux de ce mémoire ouvrent la voie à de nombreux axes de recherches :

Du point de vue théorique et expérimental, les améliorations ci-dessous sont envisageables :

- La formulation de l'équation de comportement s'est faite avec des poutres et plaques. Il serait aussi judicieux de formuler ce même comportement pour des éléments de type coque ;

- Cette même formulation s'est faite par une méthode analytique directe, il serait donc commode de formuler analytiquement un modèle éléments finis ou différences finis du comportement de la flèche en intégrant la température ;

- Identifier le renforcement maximal des fibres dans un composite pour optimiser sa flèche ;

- Vue la nature purement théorique des résultats présentés ici, il serait judicieux de mener une étude expérimentale tropicalisée. C'est pourquoi, nous proposons qu'une machine à essais dynamiques capable d'évaluer la flèche d`une structure composite sollicitée en vibration mécanique de flexion soit mise à disposition au sein du Laboratoire.

ANNEXES

Annexes 1 : Coefficients intervenants dans le calcul des fréquences propres

Tableau A1.27: Coefficients intervenants dans le calcul des fréquences propres d'un composite orthotrope (E : côté encastré ; S : côté en appui simple). [3]

Conditions aux limites

₁

₁

_2,3,4,...

_2,3,4,...

_{1 2,3,4,... 1 2,3,4,...}

^4.730

^4.730

( ^m+0.5) ( ^m+0.5)

^4.730

^Tr

^Tr

( )

ⁿ + ^0.5

^4.730

^Tr ( ^{n+0.5) Tr}

^151.3

^{12.3 c 3( c3-2)}

^{12.3 c1 (c1} - ² )

^{c1 (c1} - ^2)c3(c3-2)

		. n2?2c1?c1? 2?

Annexes 2 : Caractéristiques des fibres intégrées dans le logiciel i-VAC Tableau A2.28 : caractéristiques mécaniques et masse volumique de quelques fibres [13]

Types de fibres	Module Ef [GPa]	Contrainte à la rupture 0 fu [MPa]	Masse volumique p [kg/m3]	Module spécifique E f/p [MN.m/Kg]	Module de cisaillement G f[GPa]	Coefficient de poisson o f	Diamètre offim [lu l
Verre E	72.5	3500	2540	28.5	29.9	0.2	16
Verre R	85.5	4600	2480	34.5	35.2	0.25	10
Carbone :
?Haut module ;	390	2100	1900	205	142.9	0.35	6 à 7
?Haute résistance	240	3500	1850	130	97.7	0.3	6 à 7
Aramide (Kevlar)	130	2800	1500	87	49.3	0.37	12
Bore	385	2800	2360	146	/	/	/

Tableau A2.29 : Caractéristiques mécaniques de quelques fibres végétales extraites au Département Génie Mécanique de l'ENSET de Douala.

Types de fibres	Masse volumique p [kg/m^3]		Taux d'absorption [%]		Module d'Young Ef [GPa]		Résistance élastique Ref [MPa]		Résistance maximale RMaxf [MPa]		Allongement à la rupture [%]		Réf.
Baobab	1358		64.20		8.7 - 18.3		-		150 - 275		1.35 - 3.85		[15]				Gombo
1291- 1484	56.21		18.44 - 28.48		-		270.56 - 494.43		1.83 - 2.17		[16]
Palmier Doum		1600		63.95		14.668 - 30.118		102- 910		55- 1062		0.62 - 4.82			[17]			Kenaf
-		-		6.024 - 6.250		61- 90		122 - 150		2.3 - 2.84		[18]			Bambou V Bambou F
364.66 364.66		- -		0.49- 1.63 0.49- 1.63		9 9		13 13		0.022 0.022		[19] [20]			Palme
265.63 - 278.66		64.95- 71.72		4.33 - 8.52		-		78.23		2.5		[20]			Bananier
889 à 1055		77.47		0.179 - 2.836		1.72- 18.67		7.19 - 246.67		1.3 - 10.8		[21]
Sisal		1300-1450		-		9 - 22		-		80 - 840		1.6 - 2			[1]
RC		947		-		2.3 - 17		-		150 - 1738		10.9 - 53			[1]

Annexes 3 : Les caractéristiques des matrices intégrées dans le logiciel i-VAC Tableau A3.30 : Caractéristiques des matrices.

Types de matrices	Module Em [GPa]	Module de cisaillement Gm[GPa]	Coefficient de poisson Vm	Masse volumique Pm [kg/m^3]	Contrainte à la rupture en traction 0.???^?[MPa]	Déformation à la rupture en traction E?? ?? [%]
Résine thermodurcissable
Polyester	2,8 à 3,6	1.40	0.4	1200	50 à 85	2 à 5
Phénolique	3 à 5	1.10	0.4	1300	40	2,5
Epoxyde	3 à 5	1.33	0.3	1200	60 à 80	2 à 5
Polyimide	4 à19	1.1	0.35	1400	70	1
Résine thermoplastique
Polyamide	1,2 à 2,5	0.81 à 1.7	0.35	1140	60 à 85	200
Polypropylène	1,1 à 1,4	0.77 à 0.98	0.4	1200	20 à 35	20 à 400

Annexes 4 : Classe des moments de flexion normalisées

Les désignations SP, SD1, SD2 et SD3 représentent les types de supports. ? Supports types : SP, SD1 et SD2

Ils désignent l'ensemble des supports à section rectangulaire, carrée ou circulaire. Les dimensions standards sont :

Tableau A4.31 : caractéristiques géométriques des supports types : SP (a) ; SD1 (b) et SD2 (c) [22]

79

(a) (b) (c)

? Support type SD3

Ils désignent l'ensemble des supports en profilés normalisés I, de type IPN dont les dimensions sont normalisées et indépendantes des fournisseurs.

Tableau A4.32 : caractéristiques géométriques des supports type SD3

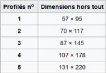
80

Pour chaque classe de moment, les fabricants de panneaux ont conçu, pour chaque catégorie de panneau (SP, SD1 ou SD2), un support résistant au moment maximal de la classe.

Tableau A4.33 : Les différentes classes des moments de flexion normalisées

Supports de signalisation directionnelle				Massifs de fondation
Moments en	SP - SD1	SD2	Support I	Catégorie A	Catégorie B
			/
			I
			I
	/
	/		/
	/		I
	/		/
	/		I
	/	/	/

Annexes 5 : Propriétés de l'acier galvanisé utilisé pour les supports de panneaux de signalisation

Tableau A5.34 : Propriétés techniques de l'acier galvanisé pour support de panneaux de

signalisation

Acier S235JR	Limite élastique	235 MPa
	Energie de rupture à 20°C	27 J/Cm^2
	Coefficient de Poisson	0,3
	Masse volumique	7800 Kg/m^3
	Module d'Young	220E+3 MPa
	Résistance à la rupture / à la traction	340 MPa

Annexes 6 : Présentation de la méthode de calcul du logiciel i-VAC

Etape 1 : Choix des constituants

Les noms des constituants intégrés dans i-VAC sont définis en annexe 2. Le code permettant de choisir les noms des constituants est :

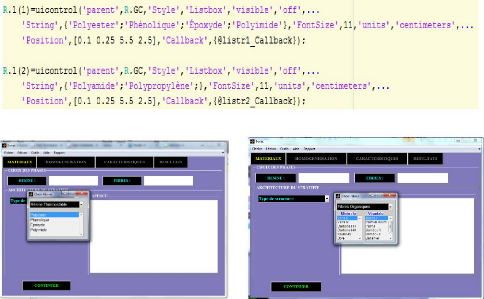
L'interface se présente comme suit au cours du choix :

Etape 2 : Choix du type d'architecture

Comme définie dans le cadre de validité §1.7, l'architecture est validée par le code :

81

L'interface se présente comme suit au cours du choix :

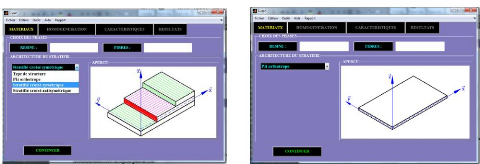
Etape 3 : Définition des caractéristiques des constituants

Les constituants choisis à l'étape 1 affiche automatiquement leurs valeurs sur l'interface HOMOGENEISATION du logiciel grâce au code :

L'interface de ce calcul pour un stratifié croisé symétrique est :

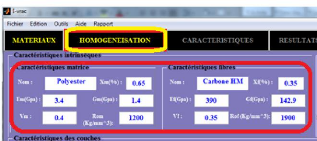
Les équations permettant de calculer les modules de l'ingénieur selon le modèle de VOIGT-REUSS sont implémentées dans le logiciel suivant le code :

82

L'interface de ce calcul pour un stratifié croisé symétrique est :

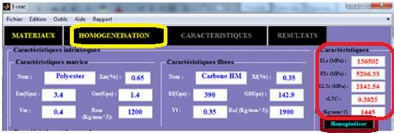
Les équations permettant de calculer les coefficients de la matrice de rigidité réduite ou matrice constitutive de la structure sont définies dans §1.2.2. (Page 5) et implémentées dans le logiciel suivant le code :

L'interface de ce calcul pour un stratifié croisé symétrique à 9 couches est :

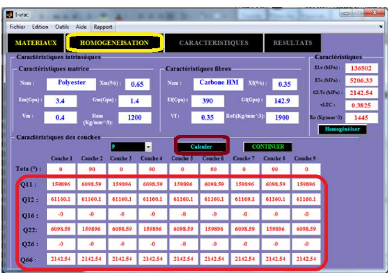
Etape 4 : Définition des caractéristiques de l'élément de structure

La matrice de rigidité réduite calculée à l'étape précédente permet de déduire les coefficients de la matrice de déflexion définies §1.3.6. (Page 11) et implémentés dans le logiciel suivant le code :

83

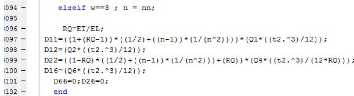
L'interface de ce calcul pour un stratifié croisé symétrique à 9 couches est :

Pour une poutre Pour une plaque

Etape 5 : Résultats

Les coefficients de la matrice de la matrice de déflexion permettent de tracer le spectre de comportement de la flèche d'un composite dont les équations sont définies dons §2.2 (cas des poutres) et §2.3 (cas des plaques). Ces équations sont implémentées dans le logiciel suivant le code :

Pour la poutre EL

84

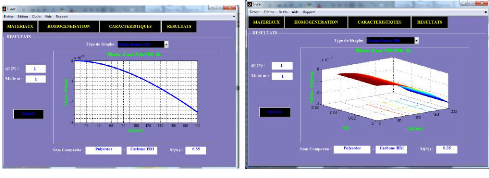
Visualisation 2D Visualisation 3D

Pour la plaque AAAA

Le logiciel de calcul i-VAC possède 3664 lignes de code.

85

86

BIBLIOGRAPHIE

[1J : RICHARD NTENGA, « Modélisation multi-échelle et caractérisation de l'anisotropie élastique de fibres végétales pour le renforcement de matériaux composites », Thèse de doctorat de UNIVERSITÉ BLAISE PASCAL(UBP) - CLERMONT II / UNIVERSITÉ DE YAOUNDÉ I (UYI), 2007 ;

[2J : A. J. ATANGANA, « Théorie des plaques de Love-Kirchhoff », notes de cours, Unité de Formation Doctorale de Douala, dispensé le 13 Janvier 2016 ;

[3J : Jean M. Berthelot, « Mécanique des matériaux et structures composites », 3^ème édition, le Mans-France, Novembre 2012 ;

[4J : R. D. Adams, D. G. C. Bacon, « Measurement of the flexure damping capacity and dynamic Young's modules of metals and reinforced plastics », Journal of physics D: Applied physics, 6, 27-41 (1973) ; [5J : S. J. Hwang, R. F. Gibson, « The use of strain energy-based finite element techniques in the analysis of various aspect of damping of composite materials and structures », journal of composite materials, 26, 2585-05 (1992) ;

[6J : B. C. Nakra, « Vibration control with viscoelastic materials- III », shock and vibration digest. 16 (5), 17-22 (1984) ;

[7J : J.C. Pascal, « Vibrations et acoustique 2 », Notes de cours, Ecole Nationale Supérieure du Mans, Université du Maine, 2008/2009 ;

[8J : F. Beténé, « Matériaux composites, polycopie de cours », Unité de Formation Doctorale de Douala, Version de Décembre 2015 ;

[9J : R. Ntenga, « Mécanique des matériaux composites part 1 », polycopie de cours, Unité de Formation Doctorale de Douala, Version de Octobre-Novembre 2010 ;

[10J : P. Vannucci, « Introduction au cours matériaux composites partie : Anisotropie et mécanique des stratifiés », Notes de cours Master 2 DSME, Ecole Nationale Supérieure du Mans, Université Versailles Saint-Quintin-en-Yvelines, Février 2007 ;

[11J : A. W. Leissa, « The free vibration of rectangular plates, Journal of sound and vibration ». 31(3), 257293 (1973) ;

[12J : Fabien BETENE, « Etude des propriétés mécaniques et thermiques du plâtre renforcé de fibres végétales tropicales », Thèse de doctorat de UNIVERSITÉ BLAISE PASCAL(UBP)- CLERMONT II / UNIVERSITÉ DE DOUALA (UD), 2012 ;

[13J : M. Assarar, A. El Mahi, J-M. Berthelot, « Analyse de la réponse dynamique des structures en matériaux composites ». 19ème Congrès Français de Mécanique. Marseille, 24-28 août 2009 ;

[14J : Lionel Gendre, « Matériaux composites et structures composites », polycopie de cours, ENS Cachan, version du 17 Mai 2011 ;

87

[15J : BASSIROU SOUAIBOU (FM5), BOFIENNE ROLAND PIERRE (FM5), « Etude d'extraction, caractérisations mécaniques et essais de conservation des fibres de l'écorce de Baobab », Mémoire de fin d'étude en vue de l'obtention du DIPET II à l'ENSET de DOUALA (2010/2011) ;

[16J : LABI TAOKREO (CM5), ABDOURAMAN DJOBI (CM5), « Extraction et caractérisation mécanique des fibres de l'écorce de la tige de gombo », Mémoire de fin d'étude en vue de l'obtention du DIPET II à l'ENSET de DOUALA (2010/2011) ;

[17J : BOUKAR OUSMAN (CM5), BAYAMA ETIENNE-MAGLOIRE (CM5), « Extraction et caractérisation mécanique des fibres de la feuille de palmier Doum, Hyphaene Thebaica », Mémoire de fin d'étude en vue de l'obtention du DIPET II à l'ENSET de DOUALA (2010/2011) ;

[18J : FEKAPING DIESSE CYRILLE (FM5), TCHIKOUA ANDRE (FM5), Extraction, description et propriétés mécaniques en traction de tissus fibreux de l'écorce de la tige de Kenaf (Hibiscus Cannabinus), Mémoire de fin d'étude en vue de l'obtention du DIPET II à l'ENSET de DOUALA (2010/2011) ;

[19J : EMATA CLOVIS (FM5), NDJING ALI (FM5), Etude du fluage des fibres de bambou de raphia (Vinefera), Mémoire de fin d'étude en vue de l'obtention du DIPET II à l'ENSET de DOUALA (2010/2011) ;

[20J : NZOKOU TALLA GATIEN (FM5), YANMO SEMO SEVERIN PATRICK (FM5), « Extraction, description physiologique et caractérisation mécanique des fibres de palmes », Mémoire de fin d'étude en vue de l'obtention du DIPET II à l'ENSET de DOUALA (2010/2011) ;

[21J : BENGONO NGWA DENISE (CM5), OLIBI RICHARD AMEDEE (CM5), « Fabrication d'un matériau composite à base de fibres de l'axe central du régime de bananier et de matrice en polymère », Mémoire de fin d'étude en vue de l'obtention du DIPET II à l'ENSET de DOUALA (2010/2011) ;

[22J : « Support & fixation », Notes d'informations du SETRA.

« La paix universelle se réalisera un jour non parce que les hommes deviendront meilleurs mais parce qu'un nouvel ordre, une science nouvelle, de nouvelles nécessités économiques leur imposeront l'état pacifique. »

Citation de Anatole France