I.6.1 .2 La Méthode des potentiels métra
(MPM)
Cette méthode a été
développée par une équipe de chercheurs
français.
1. Principe.
y' Les tâches sont représentées par
des sommets et les contraintes de succession par des arcs.
y' Chaque tâche est renseignée par la date
à laquelle elle peut commencer
(date au plus tôt) et celle à laquelle, elle
doit se terminer (date au plus tard).
y' A chaque arc est associé une valeur
numérique, qui représente soit une durée
d'opération, soit un délai. [G BAVI]
Exemple :
|
Tâche
|
Durée
|
Tâches antérieures
|
|
A
|
2
|
|
|
|
B
|
4
|
|
|
|
C
|
4
|
A
|
|
D
|
5
|
A, B
|
|
E
|
6
|
C,D
|
Tableau 1 tableau indiquant l'ordonnancement des
taches
Date au plus tôt
0
DEBUT
0
0
0
0
0
A
B
0
2
2
4
2
2
4
C
D
5
4
9
4
5
E
Date au plus tard
9
6
15
FIN
15
33
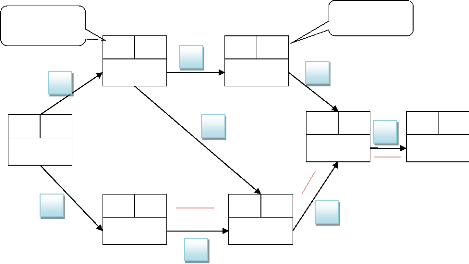
Figure 7 : Diagramme représentant La
Méthode des potentiels métra Remarques :
? La date de début au plus tôt d'une
tâche est obtenue en cumulant la durée des tâches qui
précèdent sur la séquence la plus longue.
On initialise le sommet DEBUT avec une date au plus
Tôt = 0.
Date au plus tôt de la tâche j = Max( date
au plus tôt de i + Durée Ti,j) pour tous les
prédécesseurs i de j.
? Les dates au plus tard : dates à laquelle
doivent être exécutées les tâches sans remettre en
cause la durée optimale de fin du projet.
On initialise à l'étape terminale, le
dernier sommet par la date au plus tard = date au plus tôt.
Date au plus tard i = Min (Date au plus tard de j -
durée Ti,j) pour tous les successeurs j de i.
34
y' On peut alors déterminer le chemin critique :
succession de tâches sur le chemin le plus long au sens des
durées. Pour toutes les tâches du chemin critique, les dates au
plus tôt et au plus tard coïncident. Chemin critique : B, D, E. [G
BAVI]
2. La marge totale
La marge totale sur une tâche est le retard que
l'on peut prendre dans la réalisation de cette tâche sans retarder
l'ensemble du projet.
Elle est obtenue , en faisant pour chaque tâche, la
différence entre la date au plus tard de début d'une tâche
et la date au plus tôt.
Marge totale sur A = (2-0)=2.
I.6.1 .3 Méthode P.E.R.T (Program Evaluation and
Research Task)
1. Principe.
Dans un graphe PERT :
y' Chaque tâche est représentée
par un arc, auquel on associe un chiffre entre parenthèses qui
représente la durée de la tâche.
y' Entre les arcs figurent des cercles
appelées « sommets » ou « événement »
qui marquent l'aboutissement d'une ou plusieurs tâches. Ces cercles sont
numérotés afin de suivre l'ordre de succession des divers
évènements. [G BAVI].
2. réalisation
Pour construire un graphe PERT, on utilise la
méthode des niveaux.
y' On détermine les tâches sans
antécédents, qui constituent le niveau 1.
y' On identifie ensuite les tâches dont les
antécédents sont exclusivement du niveau 1. Ces tâches
constituent le niveau 2, et ainsi de suite...[G BAVI]
Date au plus tôt
0
1
0
B(4)
A(2)
X(0)
2 4
4 4
2
3
C(4)
D(5)
9 9
4
Date au plus tard
E(6)
15 15
5
35
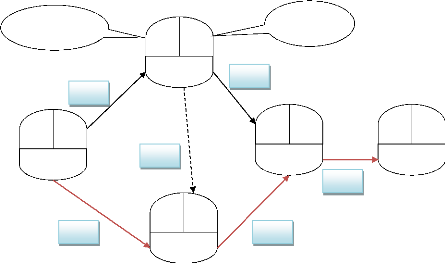
Figure 8 Diagramme qui représente la
Méthode P.E.R.T Remarques :
V' Il a été nécessaire
d'introduire une tâche fictive de durée égale à 0,
pour représenter la relation d'antériorité entre A et
D.
V' Le cumul des tâches composant la
séquence la plus longue (B, D, E) permet de déterminer la date au
plus tôt de réalisation du projet. Cette succession de
tâches constituent le chemin critique. [G BAVI].
3. Dates et marges en représentation
PERT.
V' Date au plus tôt.
On initialise la date au plus tôt du premier sommet
à 0 :
T 1 = 0 Désigne la date au plus tôt du
sommet 1.
T i = Max (T j + Durée T i,j) pour tous les
prédécesseurs j de i V' Date au plus
tard.
36
On initialise la date au plus tard du dernier sommet avec
sa date au plus tôt.
T* n = T n ( T* n : désigne la date au plus tard
du sommet n)
( T n : désigne la date au plus tôt du
sommet n).
T* i = Min ( T* j - Durée T i,j) pour tous les
successeurs j de i. [G BAVI]
? Marge totale
Marge totale i, j =T* j - T i - Durée T
i,j
T* j : est la date au plus tard du sommet j.
T i : date au plus tôt du sommet i.
T i,j : durée de la tâche entre les sommets
i et j.
|
Tache
|
A
|
B
|
C
|
D
|
E
|
|
Marges
totales
|
4-0-2=2
|
4-0-4=0
|
9-4-4=1
|
9-4-5=0
|
15-9-6=0
|
Tableau 2 les marges totales de chaque
tache
Remarque : sur le chemin critique, les marges totales des
différentes tâches sont nulles.
|
Tache
|
A
|
B
|
C
|
D
|
E
|
|
Marges libres
|
2-0-2=0
|
4-0-4=0
|
9-2-4=3
|
9-4-5=0
|
15-9-6=0
|
Tableau 3 les marges libres de chaque tache
| 


