CHAPITRE III : MÉTHODOLOGIE
3.1 Présentation de la zone
d'étude
Malgré le fait que l'altitude optimale de
développement de l'Acacia mangium est en-dessous de 300 m
(CIRAD, 2003), le peuplement étudié a été
installé depuis les mois de janvier et février de l'année
2014 en montagne à une altitude variant de 687 m à 889 m.
D'après la classification de Holdridge axée sur la zone de vie,
le site de l'étude correspond à une zone d'agriculture de
montagne humide.

Source : Google earth
Figure 1: Vue aérienne de la parcelle d'étude
3.1.1 Localisation
Le peuplement étudié est situé à
Mont-Organisé dans une localité appelée Bois Nago. Les
coordonnées géographiques du site sont comprises entre
19°24' de latitude Nord et 71°48' de longitude Ouest. La figure 2,
réalisée en fonction de la classification de Holdridge, permet
d'observer la localisation de la parcelle sur la carte d'Haïti.
12

Figure 2: Carte de localisation de la zone d'étude
3.1.2 Pluviométrie
Faute de station agro-climatologique fonctionnelle dans la
zone, les données pluviométriques recueillies sont celles
collectées par la station la plus proche du Centre Chrétien de
Ouanaminthe, située à une distance de 19 km de la zone
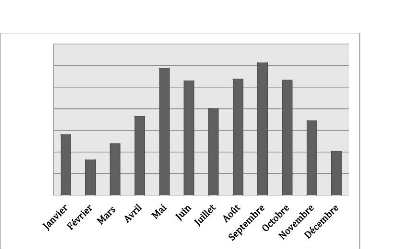
d'étude. Les figures suivantes présentent la pluviométrie
moyenne par mois (figure 3) et la pluviométrie totale par année
(figure 4) enregistrées à Ouanaminthe durant la période
1988-2019.
13
140
120
Pluviométrie (mm]
100
80
60
40
20
0

Pluviométrie (mm]
3500
3000
2500
2000
1500
1000
500
0
Figure 4: Variations annuelles de la pluviométrie
totale de Ouanaminthe (19882019)
Figure 3: Pluviométrie moyenne mensuelle de Ouanaminthe
(1988-2019)
Les mois de septembre et de mai sont les plus pluvieux avec le
maximum de précipitations moyennes (122.4 mm) enregistré au mois
septembre. Le mois de février est le moins pluvieux (32.7 mm de pluie).
A Ouanaminthe, la saison estivale est beaucoup plus arrosée
comparativement à la saison hivernale.
14
L'évolution de la pluviométrie s'est traduite
par des écarts élevés entre les années ; le maximum
(2881.2 mm) de pluie a été enregistré en 2007 et le
minimum (815.3 mm) en 1991. La courbe tendance traduit une augmentation des
précipitations avec le temps.
3.1.3 Température
Pour la même raison évoquée dans la
section précédente, les données climatiques de
température, pour la commune de Mont-Organisé sont presque
inexistantes. Il a été estimé qu'elle varie de 15 à
30°C sur toute l'année et peut descendre jusqu'à 12°C
en décembre (Valbrun, 2005).
3.1.4 Topographie et sol
Le site de l'étude est une montagne avec un relief
très élevé et dont les pentes varient de 42 à 80 %
avec une moyenne de 60 %. Les sols de Mont-Organisé sont majoritairement
rouges à dominance argileuse, constitués de l'évolution de
roches éruptives principalement basaltiques (Valbrun, 2005). Ce sont des
sols fersialitiques assez perméables dont la profondeur corrèle
avec les différentes classes de pentes. Ainsi pour les terrains à
forte déclivité comme c'est le cas pour le site de
l'étude, la profondeur est faible. Ce sont des sols très
sensibles à l'érosion.
3.1.5 Végétation et faune
Au niveau de la parcelle la végétation naturelle
est constituée de deux strates : la strate arborée
constituée d'arbre forestier énergétique : l'Acacia
mangium et la strate herbacée composée de plantes comme la
citronnelle (Cymbopogon citratus), le zèb guinen (Panicum
maximum). Quant à la faune, une observation directe a permis de
constater la présence de pintade marron (Numida meleagris), de
guêpe (Vespula vulgaris), de reptiles tel l'anolis et le
mabouillard (Ameiva chrysoloema).
3.1.6 Mode de gestion actuelle
La plantation étudiée est gérée
par une jeune association nommée ANEVERT (Action Noble pour un
Environnement Vert) chargée de prendre toutes les mesures relatives
à la protection des arbres du site. Dès le début de la
plantation, des
15
opérations de désherbage ont été
effectuées ainsi qu'un débroussaillement en amont de la parcelle.
Depuis, aucun traitement sylvicole n'a été appliqué
à la parcelle jusqu'à date. Aucun traitement n'a
été effectué sur les arbres (éclaircissage,
élagage,..) ou sur le site (amendement du sol,..), aucun
procédé de régénération (coupe progressive
régulière, coupe totale,...). Le site n'est pas
clôturé, cependant les animaux ne représentent pas une
menace au développement de la plantation.
3.2 Matériels et méthodes
3.2.1 Matériels utilisés
Les matériels utilisés pour réaliser ce
travail de mémoire sont les suivants :
V' GPS : pour la localisation des points sur le terrain
V' Appareil photographique : pour des prises de vue sur le
terrain
V' Compas forestier : pour la mesure du diamètre à
1,30 m des tiges
V' Ruban métrique : pour la mesure des distances et des
diamètres
V' Dendromètre SUUNTO : pour la mesure des angles
permettant de calculer
la hauteur des arbres et la pente du terrain
V' Fiche d'inventaire : pour la saisie des données sur le
terrain
3.2.2 Méthode de collecte des
données
Dans le cadre de cette étude, il a fallu tout d'abord
déterminer la superficie de la
parcelle. Ensuite les données qui ont été
collectées sont celles relatives à
l'inventaire ; à savoir le nombre de tiges, leur DHP et
les angles qui ont permis de
calculer la hauteur totale.
3.2.2.1 Détermination de la superficie du
site
La superficie du site a été calculée
à l'aide d'un GPS calibré de façon à enregistrer
les coordonnées du périmètre toutes les 30 secondes. Elle
a été estimée à 7,15 ha soit 71500 m2
3.2.2.2 Inventaire des arbres
3.2.2.2.1 Pré inventaire
Le pré-inventaire a été
réalisé dans la parcelle deux ans après la plantation des
arbres d'Acacia mangium. Un total de 23 arbres répartis dans 3
placettes, de 25 m2
16
chacune a été compté et mesuré. Le
coefficient de variation pour le nombre d'arbres inventoriés est
estimé à 7.44 %.
3.2.2.2.2 Plan d'échantillonnage
Pour cet inventaire on a priorisé un type
d'échantillonnage qui a permis de couvrir toute la parcelle
forestière. Et d'après une visite de reconnaissance du site,
aucune hétérogénéité n'a été
constatée. Ainsi, le choix a été porté pour un
échantillonnage systématique aléatoire car elle permet
d'avoir une meilleure estimation des variables et elle offre également
une certaine sécurité des estimations à cause de
l'uniformité de la parcelle.
V' Forme et dimension des placettes
:
Nous avons opté pour des placettes de forme circulaire
parce que selon Lecomte et Rondeux (2002), cette forme est facile à
installer et elle ne présente aucune direction
préférentielle. Et aussi, elle possède le plus petit
périmètre à surface égale ce qui limite les risques
d'erreur. La dimension des placettes quant à elle, dépend de
l'exactitude, la précision, le temps et le coût de la mesure
(Pearson et Brown, 2005). Chacune des placettes d'échantillonnage avait
un rayon (r =8 m) et (r1= 7.92 m) en tenant compte du facteur correcteur de
pente. La superficie de chaque placette calculée en appliquant la
formule s = it X r X r1 est de 198.97
m2.
V' Taux d'échantillonnage :
Pour cette étude, l'effort d'échantillonnage de
l'inventaire a été fixé à 10 %. Tenant compte du
facteur correcteur de la pente, l'échantillon a couvert une superficie
de 6963.98 m2.
V' Nombres de placettes à
échantillonner :
Le nombre de placettes d'échantillonnage est de 35. Il
a été estimé à partir du taux de sondage (f), de la
superficie totale de la parcelle (S) et de la superficie à
échantillonner (s) en appliquant la formule : n= (f×S) / s.
V' Erreur d'échantillonnage :
Le calcul de l'erreur d'échantillonnage permet de
vérifier la validité de l'échantillon. Pour un niveau de
confiance de 95 %, elle a été estimée à 2.46 %
en
17
?? × ????
appliquant la formule : e = v?? , « t »
représente le t de student, « CV » le
coefficient de variation et « n » le nombre de
placettes d'échantillonnage.
V' Répartition des placettes
d'échantillonnage :
La figure suivante montre la répartition des placettes
suivant un échantillonnage aléatoire systématique. La
première placette a été choisie au hasard et les autres
sont placées de façon systématique à une distance
moyenne de 45 m l'une de l'autre. Les coordonnées des centres des
placettes sont mentionnées en annexe.
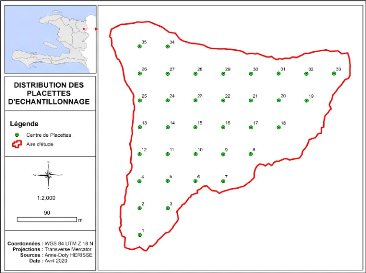
Figure 5: Distribution des placettes d'échantillonnage
3.2.2.3 Réalisation de l'inventaire
V' Équipe d'inventaire
L'équipe d'inventaire était constituée de
deux personnes, un compteur qui a implémenté les placettes et
mesuré les diamètres à hauteur de poitrines et un pointeur
qui a noté les mentions dictées par le compteur après les
avoir répétées à voix haute et qui a aussi
mesuré et noté les angles pour le calcul de la hauteur totale
ainsi que les distances entre l'arbre à mesurer et lui.
18
V' Diamètre de
précomptage
Les mesures se sont portées sur tous les arbres
d'Acacia mangium du site (âgés de 6 ans et 2 mois) dont
le DHP est supérieur ou égal à 5 cm. Les arbres vivants
comme les morts ont été mesurés.
V' Cheminement et localisation des
placettes
L'échantillonnage avait été
préalablement réalisé sur le logiciel ArcGis (version
10.2.1). Les coordonnées des centres des placettes
générées par le logiciel ont été
préalablement enregistrées dans la mémoire du
récepteur GPS. Pour localiser la première placette, il a suffi de
sélectionner le point dans le GPS, lorsque la distance était
nulle le centre était atteint. On a cheminé 45 m, toujours dans
la direction Sud-Nord afin de localiser la placette 2. Dans cette même
direction, on a parcouru toute la première rangée située
à l'ouest jusqu'à la placette 35. La placette 34 a ensuite
été localisé en cheminant la même distance dans la
direction Ouest-Est. Une fois à la 2ème rangée,
on procède de la même manière jusqu'à la placette 3,
sauf que c'est dans la direction Nord-Sud. La 6ème placette a
ensuite été localisée en parcourant 63 m dans la direction
Sud-Ouest. On a recommencé les mêmes procédures et
cheminé ainsi de suite en suite jusqu'à localiser toutes les
placettes.
V' Implantation des placettes
Une fois au centre des placettes, le compteur tend le ruban
métrique au pointeur, ce dernier mesure la distance 8 m correspondant au
rayon de la placette et marque la limite avec un piquet enfoncé dans le
sol. Cette opération avait été effectuée quatre
fois à partir du centre de chaque placette dans des directions
différentes. Ensuite le compteur fait le tour de la placette en
maintenant la ficelle tendue à un des jalons qui délimitent la
placette ou à un arbre dans certains cas.
V' Mesure des arbres
Les différentes mesures des arbres prises dans le cadre
de cet inventaire sont celles du diamètre à hauteur de poitrine
et celles permettant de calculer la hauteur totale. Pour chaque arbre des
placettes le diamètre a été mesuré à 1.30 m
en utilisant le compas forestier gradué jusqu'à 50 cm, qui a
permis d'obtenir une mesure directe du diamètre des arbres.
19
Afin de déterminer la hauteur totale le
dendromètre SUUNTO est l'instrument qui a été
utilisé, cela a impliqué de mesurer des angles. Trois cas ont
été rencontrés sur le terrain et d'après Mille et
Louppe (2015), il faut faire dans ces cas une ou deux lectures en visant soit
le sommet ou à la fois le sommet et la base de l'arbre. AB
représente la hauteur des arbres à mesurer, h la hauteur de
l'oeil de l'observateur, d la distance de l'observateur à l'arbre et
á et f3 sont les angles obtenus en visant soit le sommet ou la base de
l'arbre. Suivant les trois cas rencontrés sur le terrain, les formules
trigonométriques suivantes doivent être appliquées selon
Mille et Louppe (2015) pour déterminer la hauteur totale.
1er cas : Le terrain est horizontal et l'oeil de l'observateur
se trouve entre le sommet et la base de l'arbre, la formule appliquée a
été: AB = h + d.tgá
2e cas : Le terrain est incliné et l'oeil de
l'observateur se trouve entre le sommet et la base de l'arbre, la formule
utilisée : AB = d (tgf3 + tgá)
3e cas : Le terrain est incliné et l'oeil de
l'observateur se trouve en dessous de la base de l'arbre, alors on applique la
formule : AB = d (tgá - tgf3)
? Traitement des cas litigieux
Les cas litigieux que nous avons traités concernent ;
tout d'abord les arbres se trouvant sur la limite de la placette, alors
l'inclusion dans la placette a été faite quand plus de 3/4 de son
tronc s'est trouvé à l'intérieur de celle-ci. Ensuite, le
cas des arbres fourchus au-dessous de 1,30 m ; alors les diamètres des
différentes fourches à 1,30 m ont été
totalisés. Pour les arbres avec contreforts à 1.30 m de hauteur,
on a considéré la moyenne des circonférences
mesurées à 10 cm directement au-dessus et en-dessous de
l'anomalie. Et enfin, le cas litigieux rencontré le plus souvent lors de
la collecte des données est celui des arbres situés sur une
pente. Dans ce cas, le diamètre à hauteur de poitrine (1.30 m)
des arbres a été compté en amont du pied de l'arbre.
3.2.2.4 Calcul de la biomasse aérienne et
souterraine des arbres
3.2.2.4.1 Calcul de la biomasse aérienne
(AGB)
? Arbres vivants
Afin de déterminer la biomasse aérienne des arbres
vivants, les modèles
allométriques de Traoré et al. (2018) et de Chave
et al. (2005) ont été utilisés. Les
20
modèles allométriques développés
par Traoré et al. (2018) sont les suivants et elles ont permis
l'estimation respective de la biomasse du tronc, des branches et des
feuilles:
B1= exp(-3.228+1.681×ln(D)+1.056×ln(H))
B2 = exp(-0.865+0.498×ln(D2×H))
B3 = exp(-0.882+1.339×ln(D))
La biomasse aérienne totale a été
déterminée en additionnant la biomasse des différentes
composantes : AGB = B1+ B2+B3.
L'équation allométrique de Chave et al. (2005) a
permis une estimation directe de la biomasse. Elle a tenu compte explicitement
de la densité spécifique du bois. Pour l'espèce Acacia
mangium, la densité du bois (0.6g/cm3) a
été obtenue dans une publication faite par la FAO en 1979,
donnant des informations sur les ressources forestières. Selon Dorvil
(2010), la densité du bois à 12 % d'humidité (D12) peut
être convertie en densité spécifique du bois
séché au four à partir d'une relation
élaborée par Chave et al. (2006) à travers des
données obtenues dans des forêts tropicales : ñ = 0.872 x
D12.
L'équation allométrique de Chave et al. (2005)
applicable en forêt tropicale utilisée dans le cadre de cette
étude est la suivante:
AGB = exp(-2.557 + 0.940ln(ñD2H)) ?
0.0776×(ñD2H)0.940.
Pour cette étude, les deux résultats obtenus
pour la biomasse aérienne ont été comparés afin
d'adopter le meilleur pouvant être utilisé pour le peuplement de
Bois Nago.
? Bois morts
Se basant sur la classification faite dans le guide de mesure
et de suivi du carbone élaboré par l'USAID en 2005, les bois
morts du site appartiennent à la première catégorie :
arbre avec branches et rameaux ressemblant à un arbre vivant (sauf pour
le feuillage). La même méthode utilisée pour
déterminer la biomasse des arbres vivants a donc été
appliquée pour les arbres morts (Pearson et Brown, 2005).
NB : La biomasse des feuilles n'a pas été
calculée pour les bois morts lorsqu'il a fallu appliquer le
modèle Traoré et al. (2018).
21
3.2.2.4.2 Calcul de la biomasse souterraine
(BGB)
Selon Cairns et al. (1997), la biomasse souterraine peut
être calculée en appliquant un modèle allométrique
après avoir estimé la biomasse aérienne des arbres
mesurés. La formule suivante de Cairns et al. (1997) applicable en
forêt tropicale a été utilisée afin de
déterminer la biomasse souterraine.
BGB = 0.347 × (AGB)0.884
3.2.2.4.3 Calcul de la biomasse totale (TB)
La biomasse totale a été évaluée
en additionnant la biomasse aérienne à la biomasse souterraine
:
TB = AGB + BGB
3.2.2.5 Évaluation du stock de carbone et de la
quantité de CO2 équivalente D'après les
recommandations faites dans les directives du GIEC (2006), la fraction de
carbone couramment appliquée par défaut est de 0.47. Pour
évaluer le stock de carbone, la fraction (0.47) a été
multipliée par la biomasse.
Selon le guide de quantification des émissions de gaz
à effet de serre élaboré en 2019 par le Ministère
de l'Environnement et de la lutte contre les Changements Climatiques (MELCC) du
Québec, la quantité de dioxyde carbone (CO2) équivalente
peut être évaluée en multipliant le stock de carbone (C)
par 44/12 qui est le résultat du rapport de la masse atomique du dioxyde
de carbone à celle du carbone. C'est la méthode qui a
été appliquée dans le cadre de cette étude afin de
de déduire le stock de CO2 de celui du carbone.
Tout en respectant les règles des inférences
statistiques tous les résultats obtenus à partir de
l'échantillon ont été généralisés
à toute la population d'où l'échantillon est
tiré.
22
CHAPITRE IV : RÉSULTATS ET DISCUSSION 4.1
Inventaire du peuplement
4.1.1 Densité
Les différentes placettes inventoriées à
Bois Nago ont un total variant de 15 à 85 tiges ce qui a donné
une moyenne de 34 tiges/placette. Majoritairement (77%), les placettes
d'échantillonnage comptent de 21 à 40 tiges. La distribution du
nombre de tiges des placettes est donc très
hétérogène. Afin de mieux apprécier la
densité du peuplement, la carte suivante représente par des
boules le nombre de tiges des différentes placettes. Ainsi les endroits
plus ou moins denses du peuplement sont localisés.
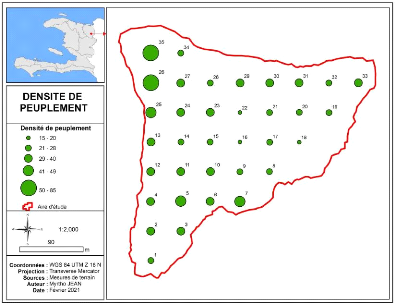
Figure 6: Carte présentant la densité du peuplement
de Bois Nago
Le peuplement est plus dense au Nord-Ouest à
l'extrémité de la parcelle d'où la pente est plus raide
tandis qu'à l'Est la densité est plus faible car le nombre de
tiges des placettes varie de 15 à 20 (figure 6). Le nombre de tiges de
chaque placette a été ramené à l'hectare (tableau
6), et le coefficient de variation ainsi que
23
les valeurs minimum et maximum de densité montrent que
la densité moyenne du peuplement n'est pas représentative de
celle de toutes les placettes. Le coefficient de variation des arbres morts est
plus élevé, cette distribution est donc très
hétérogène comparativement aux arbres vivants. Les arbres
morts ne représentent qu'1 % de la population, les résultats de
cette distribution n'influencent pas beaucoup la distribution totale comprenant
les deux catégories d'arbres. Le tableau suivant présente la
densité du peuplement à l'hectare :
Tableau 6: Densité du peuplement d'Acacia mangium
de Bois Nago à l'hectare
|
Densité
|
Effectif
|
Moyenne/ ha
|
Coefficient
de variation
|
Erreur-type
|
Min
|
Max
|
|
Arbres vivants
|
1180
|
1694
|
0.40
|
226
|
704
|
4272
|
|
Arbres morts
|
9
|
13
|
3.98
|
17
|
0
|
302
|
|
Tous
|
1189
|
1707
|
0.39
|
222
|
754
|
4272
|
Le peuplement est beaucoup plus dense que ceux qui ont
été mentionnés dans la littérature et dans
l'étude de l'hypothèse en se référant aux travaux
réalisés par Herdiyanti et Sulistyawati (2009), Hériansyah
et al. (2007), Ilyas (2013) et Traoré et al (2018) dans des peuplements
d'Acacia mangium âgé respectivement de 5, 5.5 et 7 ans.
Ces écarts s'expliquent par le fait que les objectifs de plantation
diffèrent de celui de Bois Nago qui a été principalement
de couvrir le sol préalablement dénudé. De plus, le
peuplement étudié n'a bénéficié d'aucun
traitement sylvicole à la différence de ceux de la
littérature.
4.1.2 Diamètre à hauteur de
poitrine
? Structure diamétrique du
peuplement
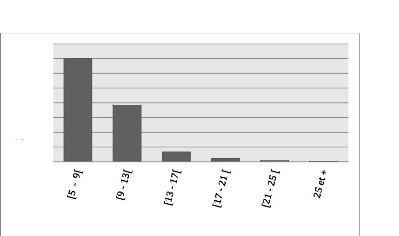
Les diamètres des tiges (arbres morts y compris)
varient de 5 cm à 29 cm et ont été regroupés en 6
classes de 4 cm d'amplitude. Les tiges de classe [5 cm, 9 cm) et [9 cm, 13 cm)
sont en plus grande proportion à Bois Nago et représentent
à eux seuls 91.34 % de la distribution avec la fréquence de tiges
la plus élevée (701) enregistrée dans la classe [5 cm, 9
cm). Cette distribution est illustrée par le diagramme en barres
ci-dessous :
24
Classes de diamètre (cm)
800
700
Nombre de tiges
600
500
400
300
200
100
0
Le DHP moyen du peuplement étudié est
très faible par rapport à celui (23.4 cm) de l'étude de
l'hypothèse réalisé par Traoré et al. (2018).
Quoiqu'âgé de 7 ans, la
Figure 7: Histogramme montrant le nombre de tiges par classe de
diamètre
La distribution diamétrique du peuplement montre
qu'à Bois Nago les tiges de petits diamètres dominent, la forte
présence de ces individus pourrait être justifiée par la
densité trop élevée des tiges qui implique un espacement
trop petit entre les arbres. En effet, l'augmentation de la densité
réduit la croissance en diamètre des arbres (Fonton et al., 2002;
Tonini et al., 2018; Prégent, 1998). Les DHP mesurés
présentent une asymétrie positive et une distribution
générale en forme de « J » inversé, traduisant
un peuplement jeune et non exploitable. D'après le tableau 7, la
dispersion de la distribution du DHP des arbres morts et des arbres vivants est
presque similaire puisque le coefficient de variation présente seulement
une différence de 2 %, cependant la distribution du DHP des arbres
vivants est plus proche du DHP moyen.
Tableau 7: DHP du peuplement d'Acacia mangium de Bois
Nago
|
DHP (cm)
|
Effectif
|
Moyenne
|
Coefficient de variation
|
Erreur-type
|
Min
|
Max
|
|
Arbres vivants
|
1180
|
8.82
|
0.36
|
0.18
|
5
|
29
|
|
Arbres morts
|
9
|
9.04
|
0.34
|
1.99
|
5.40
|
14.90
|
|
Tous
|
1189
|
8.83
|
0.36
|
0.18
|
5
|
29
|
25
différence est énorme par rapport au DHP moyen
du peuplement étudié, deux principales raisons expliquent ces
écarts ; tout d'abord, à Bois Nago les tiges évoluent en
exerçant une forte concurrence entre elles surtout par rapport aux
ressources limitées, ce qui a conduit à l'obtention des tiges de
faibles diamètres. Ensuite, l'absence d'application de technique
sylvicole, notamment l'éclaircissage qui selon Prégent (1998) est
très utile pour obtenir du bois de grosses dimensions.
4.1.3 Surface terrière
La surface terrière des arbres varie de 0.002
m2 à 0.066 m2. Répartie entre les
différentes classes de diamètre, elle varie de 3.25 m2
à 0.22 m2. La distribution de la surface terrière
occupée par les arbres de chaque classe de diamètre est
présentée par l'histogramme ci-dessous.
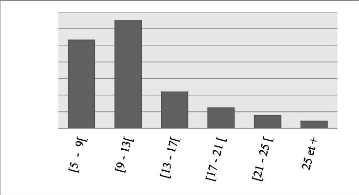
Surface terrière (m2)
2.5
0.5
3.5
1.5
2
0
3
1
Classe de diamètre (cm)
Figure 8: Histogramme présentant la surface
terrière par classe de diamètre
Les arbres de la classe [9 cm, 13 cm) occupent la plus grande
surface terrière quoiqu'elle ne compte pas le plus grand nombre de
tiges. Cependant le DHP des arbres qui représentent cette classe est
plus élevé par rapport à la première classe. Les
tiges de plus gros diamètres de ce peuplement obtiennent les faibles
valeurs de surface terrière car elles sont en plus petites proportions.
Nos résultats confirment les affirmations de Prégent (1998)
stipulant que la surface terrière est un paramètre tenant
à la fois compte de la grosseur et du nombre de tiges. La surface
terrière obtenue par les différentes catégories d'arbres
de chaque placette a été ramenée à
26
l'hectare (tableau 8). Les résultats montrent que les
arbres vivants occupent la plus grande surface terrière à Bois
Nago comparativement à celle des arbres morts. Les valeurs totales et
moyennes de la surface terrière du peuplement sont
présentées dans le tableau ci-dessous :
Tableau 8: Surface terrière du peuplement
|
Surface
terrière (m2/ha)
|
Effectif Total Moyenne Coefficient Erreur-
de variation type
|
Min Max
|
|
Arbres vivants
|
1180
|
11.67
|
0.33
|
0.31
|
0.03
|
0.15
|
0.55
|
|
Arbres morts
|
9
|
0.09
|
0.003
|
4.71
|
0.004
|
0
|
0.074
|
|
Tous
|
1189
|
11.77
|
0.34
|
0.30
|
0.03
|
0.15
|
0.55
|
Nos résultats corroborent avec celui (11.1
m2/ha) trouvé par Dupuy et N'Guessan (1990) pour un
peuplement d'Acacia mangium âgés de 5 ans. Cependant, par
rapport à l'étude de l'hypothèse réalisée
par Traoré et al. (2018) la surface terrière du peuplement de
Bois Nago corrobore à celui de 3 ans estimée à (10.42
m2/ha) mais elle est beaucoup plus faible que celle
(30.75m2/ha) du peuplement de 7 ans.
4.1.4 Hauteur totale
Les résultats de cette étude montrent que la
hauteur totale des arbres au niveau du site est non uniformément
répartie, elle oscille entre 4.87 m et 27.62 m. La variabilité de
la distribution est illustrée par la boîte à moustache
ci-dessous.
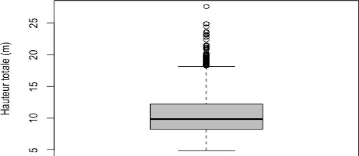
Figure 9: Boite à moustache présentant la
distribution de la hauteur totale du peuplement
27
La boîte à moustache (figure 9) montre une
distribution asymétrique car la valeur de la médiane (9.84 m) est
inférieure à la hauteur moyenne (10.70 m). En plus de cela, 75 %
des arbres ont une hauteur totale supérieure à 8.24 m. La
boîte à moustache permet également de constater que la
hauteur totale du peuplement de Bois Nago présente un bon nombre de
valeurs extrêmes et une valeur aberrante. Et d'après le tableau 9,
les arbres vivants affichent un coefficient de variation plus
élevé, qui traduit une plus forte dispersion de la distribution
de la hauteur totale des arbres vivants comparativement aux arbres morts. La
hauteur totale dominante c'est-à-dire la hauteur moyenne des 100 plus
hauts arbres à l'hectare du peuplement ainsi que la hauteur totale
moyenne est présentée dans le tableau 9:
Tableau 9: Hauteur totale du peuplement
|
Hauteur totale (m)
|
Effectif
|
Hauteur dominante
|
Moyenne
|
Coefficient de variation
|
Erreur-type
|
Min
|
Max
|
|
Arbres vivants
|
1180
|
20.01
|
10.70
|
0.33
|
0.20
|
4.87
|
27.62
|
|
Arbres morts
|
9
|
-
|
9.08
|
0.21
|
1.24
|
6.47
|
12.73
|
|
Tous
|
1189
|
-
|
10.69
|
0.33
|
0.20
|
4.87
|
27.62
|
La valeur moyenne de la hauteur totale du peuplement
étudié est inférieure à celle (18.95 m) de
l'étude de l'hypothèse pour le peuplement de 7 ans. Il en est de
même pour le peuplement de 3 ans dont la hauteur moyenne est de 12.58 m.
Nos résultats se rapprochent plutôt de celle trouvée dans
une étude réalisée par Dupuy et N'Guessan (1990) pour un
peuplement d'Acacia mangium âgé de 5 ans. Le rapport
entre la hauteur moyenne et le DHP moyen du peuplement de Bois Nago donne un
facteur d'élancement égal à 121, cela traduit selon
Massenet (2010) que le peuplement est très fragile et à ce stade,
un éclaircissage pourrait augmenter le risque de chablis.
4.2 Biomasse
4.2.1 Biomasse aérienne avec l'équation de
Chave et al. (2005)
En appliquant l'équation de Chave et al. (2005), les
résultats obtenus pour la biomasse aérienne totale de
l'échantillon inventorié est de 34.96 tonnes. Ramené
à
28
l'hectare (tableau 10), chaque placette a une quantité
de biomasse variant de 18.22 t/ha à 87.53 t/ha. La biomasse des
placettes n'ayant aucun arbre mort est estimée à 0 t/ha. Les
résultats trouvés en moyenne par catégorie sont
présentés dans le tableau suivant :
Tableau 10: Biomasse aérienne du peuplement
calculée à partir de l'équation de Chave et al. (2005)
|
Biomasse aérienne (t/ha)
|
Effectif
|
Moyenne
|
Coefficient de variation
|
Erreur-type
|
Min
|
Max
|
|
Arbres vivants
|
1180
|
50.21
|
0.39
|
6.43
|
18.22
|
87.53
|
|
Arbres morts
|
9
|
0.33
|
4.94
|
0.54
|
0
|
9.71
|
|
Tous
|
1189
|
50.54
|
0.38
|
6.39
|
18.22
|
87.53
|
D'après les valeurs de coefficient de variation des
deux catégories d'arbres, la distribution de la biomasse aérienne
des arbres vivants est beaucoup plus homogène. Cependant, ces derniers
ne représentent que 0.66 % de la biomasse aérienne du site, cela
explique le fait que ces résultats n'influencent pas trop la
distribution totale pour laquelle le coefficient de variation est sensiblement
égal à celui des arbres vivants. Comparativement aux
résultats (63.47 t/ha) de l'étude réalisée par
Hériansyah et al. (2007) dans un peuplement d'Acacia
mangium de 7 ans, la biomasse du peuplement de Bois Nago est moins
élevée. Le résultat est également inférieur
à la valeur (90 t/ha) présentée par Aalde et al. (2006)
pour les plantations de forêt du système montagneux tropical dans
les lignes directrices 2006 du GIEC pour les inventaires nationaux de gaz
à effet de serre.
4.2.2 Biomasse aérienne avec l'équation
de Traoré et al. (2018)
La biomasse aérienne totale des arbres
échantillonnés en appliquant l'équation de Traoré
et al. (2018) est de 50.34 tonnes, dont les arbres vivants constituent 99.45 %
de ce stock. Les résultats trouvés pour chaque placette ont
été ramenés à l'hectare et la biomasse
aérienne a été estimée à une valeur moyenne
par placette de 72.68#177;8.15 t/ha. La biomasse aérienne du peuplement
par catégorie ainsi que
29
les valeurs minimum et maximum des placettes
échantillonnées sont présentées dans le tableau
ci-dessous :
Tableau 11: Biomasse aérienne du peuplement
calculée à partir de l'équation de Traoré et al
(2018)
|
Biomasse aérienne (t/ha)
|
Effectif
|
Moyenne
|
|
|
CV
|
Erreur-type
|
Min
|
Max
|
|
T
|
B
|
F
|
BA
|
|
|
Arbres vivants
|
1180
|
37.74
|
20.93
|
13.62
|
72.29
|
0.34
|
8.25
|
29.36
|
122.96
|
|
Arbres morts
|
9
|
0.24
|
0.15
|
0
|
0.39
|
4.78
|
0.62
|
0
|
11.16
|
|
Tous
|
1189
|
37.98
|
21.08
|
13.62
|
72.68
|
0.34
|
8.15
|
29.36
|
122.96
|
T : Tronc, B : branches, F : feuilles, BA : biomasse
aérienne, CV : coefficient de
variation
Le coefficient de variation des arbres morts étant plus
élevé, cela traduit que la distribution de la biomasse
aérienne des arbres morts est beaucoup plus dispersée. Le
résultat trouvé en appliquant l'équation de Traoré
et al. (2018) est supérieur aux résultats de l'étude
réalisée par Hériansyah et al. (2007) dans le peuplement
d'Acacia mangium de 7 ans ; mais inférieur à la valeur
présentée par Aalde et al. (2006) pour les plantations du
système montagneux tropical.
4.2.3 Comparaison des résultats de la biomasse
aérienne
Le premier modèle d'équation allométrique
appliqué c'est-à-dire celui de Chave et al. (2005) a permis
d'obtenir des résultats plus faibles comparativement au second
modèle, celui de Traoré et al. (2018). Le coefficient de
variation obtenue de la distribution de la biomasse aérienne à
partir de l'équation de Chave et al. (2005) est de 2 % plus
élevé que celui de Traoré et al. (2018), cela traduit que
la distribution des résultats de l'application du premier modèle
est plus dispersée autour de la moyenne. Les raisons expliquant cette
différence dans les résultats de l'application des deux
modèles sont le fait que : d'une part, l'équation de Chave et al.
(2005) fait une estimation directe de la biomasse aérienne et est
applicable aux zones de forêts tropicales humides, la
réalité écologique du site étudié y a donc
été
30
prise en compte. Ce modèle considère
également la densité spécifique du bois, en plus du DHP et
de la hauteur totale, ce qui permet d'avoir une meilleure précision des
estimations. D'autre part, l'équation de Traoré et al. (2018) a
permis une estimation séparée de la biomasse de chaque
compartiment aérien (tronc, branches, feuilles) des arbres afin de
calculer la biomasse aérienne, d'où une surestimation des valeurs
par rapport aux précédents modèles. De plus, c'est un
modèle développé seulement pour un site en Côte
d'Ivoire dont les réalités climatiques et d'altitudes
décrites dans la section 2.2.3, sont très différentes de
Bois Nago. Ainsi, le modèle qui convient le mieux dans le cadre de cette
étude est l'équation développée par Chave et al.
(2005) et c'est celui dont les résultats ont été
utilisés afin de poursuivre le travail.
4.2.4 Biomasse souterraine
La biomasse souterraine de l'échantillon a
été estimée à 7.92 tonnes au total. Convertie
à l'hectare elle varie entre les placettes de 4.35 t/ha à 19.06
t/ha. La biomasse souterraine du peuplement à l'hectare est
présentée dans le tableau suivant :
Tableau 12: Biomasse souterraine du peuplement
|
Biomasse
souterraine (t/ha)
|
Effectif
|
Moyenne
|
Coefficient de variation
|
Erreur-type
|
Min
|
Max
|
|
Arbres vivants
|
1180
|
11.37
|
0.36
|
1.37
|
4.35
|
19.06
|
|
Arbres morts
|
9
|
0.08
|
4.85
|
0.12
|
0
|
2.22
|
|
Tous
|
1189
|
11.45
|
0.36
|
1.35
|
4.35
|
19.06
|
Étant donné que c'est un seul et même
échantillon et que la biomasse souterraine est étroitement
liée à la biomasse aérienne, les constats sont pareils. En
effet, la distribution de la biomasse des arbres vivants est beaucoup plus
homogène. Comparativement aux études de la littérature
(tableau 2) dont les résultats de la biomasse aérienne sont plus
élevés ou plus faibles à celle de Bois Nago, la biomasse
souterraine du peuplement étudié sera plus faible et
inversement.

Biomasse totale (t/ha)
120
100
40
80
60
20
0
0 1000 2000 3000 4000 5000
Densité
y = 0.0144x + 37.439 R2 = 0.1709
Figure 10: Diagramme de corrélation entre la biomasse et
la densité du peuplement
31
4.2.5 Biomasse totale
La biomasse totale de l'échantillon est de 42.88 tonnes.
Les résultats ramenés à l'hectare sont
présentés dans le tableau 13 et ils montrent à partir de
l'erreur-type, une différence de 7.73 t/ha si tous les arbres du
peuplement avaient été mesurés.
Tableau 13: Biomasse totale du peuplement
|
Biomasse totale (t/ha)
|
Effectif
|
Moyenne
|
Coefficient de variation
|
Erreur-type
|
Min
|
Max
|
|
Arbres vivants
|
1180
|
61.58
|
0.38
|
7.79
|
22.57
|
105.64
|
|
Arbres morts
|
9
|
0.40
|
4.92
|
0.66
|
0
|
11.93
|
|
Tous
|
1189
|
61.98
|
0.38
|
7.73
|
22.57
|
105.64
|
La biomasse aérienne représentant 81.53 % de la
biomasse totale influence davantage les résultats que la biomasse
souterraine d'où la similitude du coefficient variation de la biomasse
aérienne avec celui obtenu pour la biomasse totale.
4.2.6 Relation entre la biomasse totale et la
densité
Comme vu dans la section 4.1.1, la densité du
peuplement d'Acacia mangium de Bois Nago est élevée et
de plus très hétérogène. La relation existant entre
la biomasse de ce peuplement et la densité de plantation est
illustrée par le diagramme ci -dessous :
32
Chaque nuage de point de la figure 10 représente la
biomasse totale et la densité de chaque placette. On peut constater que
la densité la plus élevée ne correspond pas au plus grand
stock de biomasse. La figure 10 montre également que la relation entre
la biomasse et la densité n'est pas linéaire car les nuages de
point n'ont pas la forme d'une ligne. Etant donné que certains points de
la figure sont proches et que d'autres sont éloignés, on peut
dire que la relation entre la biomasse et la densité est
modérée et le signe du coefficient de corrélation indique
une relation positive. Donc on peut conclure que les résultats de cette
étude montrent qu'il existe effectivement une relation, quoique non
linéaire entre la biomasse et la densité du peuplement, mais ce
dernier paramètre n'influence pas à lui seul le stock de biomasse
trouvé pour le peuplement d'Acacia mangium de Bois Nago.
4.3 Stock de carbone et quantité de CO2
équivalente
Le stock de carbone total de l'échantillon est
évalué à 20.29 tonnes. La distribution des données
de stock de carbone présente presque les mêmes
caractéristiques (sauf pour l'erreur-type) que celle de la biomasse
aérienne, souterraine et totale à partir desquelles a
été évalué le stock de carbone. Les valeurs
moyennes à l'hectare par placette sont présentées dans le
tableau suivant :
Tableau 14: Stock de carbone du peuplement
|
Stock de carbone (t/ha)
|
Moyenne Coefficient
de variation
|
Erreur-type
|
Min Max
|
|
Partie aérienne
|
23.75
|
0.38
|
3.00
|
8.56
|
41.14
|
|
Partie souterraine
|
5.38
|
0.34
|
0.64
|
2.05
|
8.96
|
|
Totale
|
29.13
|
0.38
|
3.63
|
10.61
|
49.65
|
Le stock moyen de carbone du peuplement de Bois Nago
(29.13#177;3.63 t/ha) est inférieur à la quantité (86.33
t/ha) stockée par le peuplement d'Acacia mangium de 7 ans de
l'étude réalisée par Traoré et al. (2018)
mentionnée dans notre hypothèse, il est également
inférieur au stock de carbone (53.72 t/ha) préconisé par
Aalde et al. (2006). Lorsqu'on compare le résultat de l'étude de
Traoré et al. (2018) à celle de Bois Nago, les deux raisons
suivantes pourraient expliquer les écarts observés.
Comparativement à la valeur (139.8 t/ha) de l'étude
réalisée par Jean Baptiste
33
? La forte abondance des tiges de plus petits diamètres
au niveau du peuplement ; 50 % des arbres ont un diamètre
inférieur à 9 cm et une hauteur inférieure à 10 m.
Le stock de carbone est étroitement lié à la biomasse, or
les individus de petits diamètres représentent selon Mille et
Louppe (2015) une faible fraction de la biomasse aérienne ; d'où
le faible stock de carbone.
? La différence des conditions écologiques et
d'âge du peuplement de Traoré et al. (2018) à celui de Bois
Nago. En effet, le peuplement étudié par Traoré et al.
(2018) âgé 7 ans, est situé à une altitude variant
de 40 à 100 m, plus favorable au développement de
l'espèce, car l'altitude optimale de développement de
l'espèce est en-dessous de 300 m (CIRAD, 2003). La croissance des arbres
diminuent dans les conditions peu favorables dont l'altitude, ce qui entraine
une faible portion de la biomasse et par la même occasion un faible stock
de carbone. Des auteurs dont, Fayolle et al (2013), Ifo et al. (2018), Ifo et
Binsangou (2019), Mugnier et al. (2009) ont effectivement observées des
variations du stock de carbone selon l'altitude, le microclimat et l'âge
de la forêt.
Par rapport à la valeur présentée par
Aalde et al. (2006), les lignes directrices du GIEC sont très peu
explicites quant à la méthode utilisée pour
déterminer la biomasse dont dépend le stock de carbone, mais
confirment que ce ne sont que des valeurs approximatives. De plus ces
études ont été réalisées à
très grande échelle et l'absence de données pour les
régions d'un pays donne parfois lieu à des omissions. A
côté de cela, la nature des sources de données peut
être à l'origine des incertitudes, car les méthodes du GIEC
sont généralement basées sur des données existantes
mises à jour périodiquement (GIEC, 2003). Or à nos jours
une base de données sur les inventaires forestiers en Haïti est
pratiquement inexistante, ce qui écarte encore davantage la
possibilité que la valeur approximative d'Aalde et al. (2006)
corresponde à la réalité de Bois Nago. Dans cette
étude, les données ont été collectées
directement sur le terrain par échantillonnage systématique, ce
qui permet d'avoir une bonne précision des estimations du stock de
carbone.
34
(2018) dans un peuplement multispécifique, le stock de
carbone du peuplement d'Acacia mangium est beaucoup moins
élevé. En effet, la méthodologie appliquée dans les
deux études est similaire car il a été question
d'appliquer des modèles d'équations allométriques
généralisées. Cependant, le peuplement
étudié par Jean Baptiste (2018) a un DHP très
appréciable, qui va au-delà de 100 cm pour certains arbres et de
plus, 40 % du peuplement a une hauteur qui dépasse 20 m. Contrairement
au jeune peuplement d'Acacia mangium qui est monospécifique et
dont moins de 2 % des arbres ont une hauteur qui dépasse 20 m et le DHP
du peuplement est compris seulement entre 5 cm et 29 cm. D'où la raison
expliquant le faible stock de carbone du peuplement d'Acacia mangium
de Bois Nago par rapport au peuplement de l'étude de Jean Baptiste
(2018).
La quantité de CO2 du site a été
déduite directement du stock de carbone total. Les résultats
trouvés pour le peuplement de Bois Nago sont présentés
dans le tableau suivant :
Tableau 15: Quantité de CO2 équivalente du
peuplement
Stock de carbone Quantité moyenne de CO2 Min Max
total
29.13#177;3.63 106.82#177;16.32 38.90 182.06
Nos résultats montrent que le peuplement de Bois Nago
est capable de stocker 106.82#177;16.32 t/ha de CO2. Toujours est-il que ce
stock est faible par rapport à celui de l'étude de Traoré
et al. (2018) car il a été déduit du stock de carbone.
Selon la banque mondiale (2016), chaque habitant du pays émettait par an
0.3 tonne de CO2, ce qui fait que cette plantation est capable de stocker
l'équivalent de CO2 émise annuellement par 2545 habitants.
35
| 


