Contributions des couts logistiques du transport à la réforme de l'entreprise.

V.2.35. Tableau XXIII. STATISTIQUE DE REPARTITION DES COUTS DE
TRANSPORT ET DU CHIFFRE D'AFFAIRES DE 2009-2013

ANNEES	COUT DE TRANSPORT (X)	CHIFFRE D'AFFAIRES (Y)
2009	1 268 966700 FC	20 981 007 000 FC
2010	1 532 465 100 FC	66 099 515 400 FC
2011	1 627 830 900 FC	69 161 162 400 FC
2012	1 810 861 200 FC	68 195 482 200 FC
2013	1 471 966 200 FC	86 465 231 300 FC

Source: Conçu à partir des données des tableaux XVIII et XXII V.2.36. Tableau XXIV. CALCUL DES VARIABLES

ANNEES	X(en milliards des FC)	Y(en milliards des FC)	XY	X2	Y2
2009	1,268	20,981	26,603908	1,607824	440,202361
2010	1,532	66,099	101,263668	2,347024	4369,077801
2011	1,627	69,161	112,524947	2,647129	4783,243921
2012	1,81	68,195	123,43295	3,2761	4650,558025
2013	1,471	86,465	127,190015	2,163841	7476,196225
TOTAL	7,708	310,901	491,015488	12,041918	21719,27833

Source: Conçu par l'auteur à partir de deux variables X et Y

Comme nous l'avions prédit au départ, la variable X représente les couts de transport et la variable Y représente le chiffre d'affaires généré durant toute la période d'exercice relative à notre étude.

Se servant de la méthode statistique qui nous montre que l'étape principale d'une analyse de régression consiste à déduire, en se basant sur les données échantillonnages, une équation d'estimation qui décrit la nature fonctionnelle de la relation entre les variables nous allons déterminer la relation statistique existant entre les deux variables de notre étude X et Y pour lesquelles une représente le couts du transport et l'autre représente le chiffre d'affaires.

Pour ce faire, SANDERS et ALLAND nous propose la formule de déduction suivante:

,350

105

e de l'échantillon

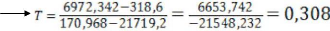
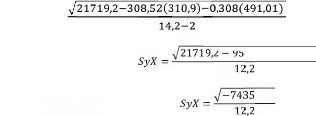
Alors SyX=

2 95918,8 - 151,23

0,83

D'où la constante a une valeur résiduelle de 0,308

Sachant que A=Y-(tx)= 310,901-(0,308)(7,708)

A=310,901-2,374

A=308,52

V.2.37. CALCCUL DE L'ERREUR DE TYPE D'ESTIMATION

Le calcul de l'erreur type d'estimati ur l l di d régression.

Dans ce cas, la moyenne d centrale.

Sachant que y²=21719,27833 ; X= 7,708 ;

Y= 310,901 ;

A=308,52

106

V.2.38. ANALYSE DU COEFFICIENT DE DETERMINATION COMME CORRELATION ENTRE DEUX VARIABLES

Le coefficient de détermination est une mesure de la proportion de la variation de la variable Y qui s'explique par la présence de la variable X. C'est aussi le carré du coefficient de corrélation de l'économiste KANDELL.

Cela éant p o transport, le coefficient de détermination (r²) se calcule de la façon ci-

après

²

R²=

(

R²=

R²=

R²=

R²= 5,19

Nous venons de constater que le coefficient de détermination se situe entre 4 et 6. Ce qui nous ramène à confirmer que le modèle est significatif. Lorsque le modèle s'avère significatif la corrélation est forte, cela veut dire qu'il ya une relation entre croissance du chiffre d'affaires et les couts liés au transport.

Ceci vérifie une partie de notre deuxième hypothèse et nous permet de confirmer ainsi l'hypothèse selon laquelle « l'élaboration d'un programme optimal d'approvisionnement des matières premières et de la distribution des produits par la gestion du transport peut-elle contribuer à la reforme du chiffre d'affaires au sein de l'entreprise qu'est la Bralima Sarl/Siège de Bukavu ».