2.3.2 Estimation du modèle
Dans la section précédente nous avons validé
la stationnarité des séries de notre modèle. Nous allons
présenter par la suite les résultats de l'estimation d'une part,
d'autre part nous testerons la validité de ce modèle.
2.3.2.1 Résultats de l'estimation
Après avoir transféré notre base de
données d'un fichier Excel à Eviwes, l'estimation nous offre le
résultat suivant :

IDE=cst+ c1CHOM+c2CRO+c3ABM+c4OUV+c5R+c6SEC+c7RD+c8FISC
+c9INF+c10SPAV+c11QR+c12CC+? t
Avec :
IDE : IDE en % du PIB INF : indice prix à la
consommation
CHOM : taux de chômage SEC : taux de scolarisation
secondaire
SPAV : stabilité politique et absence de la violence
CC : contrôle de la corruption FISC : recettes fiscaux
OUV : ouverture commerciale QR : qualité de
réglementation
RD : chercheurs en R&D CRO : taux de croissance de PIB
ABM
: abonnés à la téléphonie mobile
? t : Terme d'erreur Ci : Coefficient attribué aux
variables
65
Nous résumons les résultats de l'estimation (annexe
2), dans le tableau ci-dessous
66
Tableau 11: Résultats de
l'estimation
|
Coefficient Std-Error t-statsitic Prop
|
C(1)
|
-0.357822
|
0.213173
|
-1.678549
|
0.1115
|
C(2)
|
0.249388
|
0.089872
|
2.774928
|
0.0130
|
C(3)
|
0.110210
|
0.022713
|
4.852281
|
0.0001
|
C(4)
|
-0.013415
|
0.091390
|
-0.146792
|
0.8850
|
C(5)
|
0.501001
|
2.757752
|
0.181670
|
0.8580
|
C(6)
|
0.063690
|
0.139341
|
0.457076
|
0.6534
|
C(7)
|
-0.002529
|
0.001317
|
-1.919525
|
0.0719
|
C(8)
|
0.123864
|
0.290253
|
0.426745
|
0.6749
|
C(9)
|
0.064642
|
0.125915
|
0.513375
|
0.6143
|
C(10)
|
2.104096
|
0.943153
|
2.230916
|
0.0394
|
C(11)
|
8.708339
|
5.059518
|
1.721180
|
0.1034
|
C(12)
|
|
3.364593
|
1.744305
|
1.928902
|
0.0706
|
|
R-Squared : 0.800819 F-statistic : 5.257655
Prob(F-statistic) : 0.000960
2.3.2.2 Validation du modèle
Afin d'obtenir un modèle adéquat globalement
significatif et que nous garantit une
meilleure régression, il faut répondre à
quatre conditions. Celles -ci se résument comme suit :
V' Avoir une valeur importante de R-Squared
V' Les résidus ne doivent pas être
corrélés
V' Absence d'hétéroscédasticité
V' Les résidus doivent avoir une distribution normale
2.3.2.2.1 analyse de normalité
L'analyse commence en effectuant un test de normalité
pour les variables à travers le
test de JarqueBera qui suit une loi de (X2), ce test
évalue les écarts simultanés de ces
coefficients avec les valeurs de référence de la
loi normale.
hypothèse du test:
H0 : les résidus suivent une loi
normale
H1 : les résidus ne suivent pas une loi
normale
67
Règle de décision : accepter
l'hypothèse nulle si P-Vlue de JarqueBera est supérieur à
5%.
Figure 6 : Test de normalité de
JarqueBera
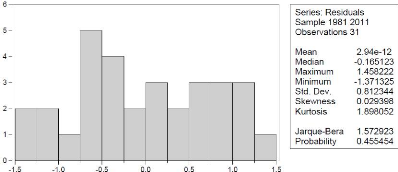
Le test JarqueBera sur Eviwes(7) nous offre un P-value de
0.455454>5%. Par conséquent la majorité des variables suivent
une loi normale ce qui autorise l'estimation par la méthode MCO.
2.3.2.2.2 l'autocorrélation des résidus
:
Le problème d'autocorrélation des résidus
doit être testé dans le but de vérifier l'existence
d'un bruit blanc qui correspond à « une suite des
variables aléatoire de même distribution et
mutuellement indépendantes. »36.
Hypothèse du test:
H0 : les résidus ne sont as
autocorrélés
H1 : les résidus sont
autocorrélés
Règle de décision :
Accepter H0 si P-Value de Chi Square est supérieur
à 5%.
36Bourbonnais_économétrie 2015 -
9ème édition - 392 pages - 155x240 mm EAN13 : 9782100721511
EAN13 : 9782100721511
68
Tableau 12 : test d'autocorrélation des
résidus

F-statistic 0.024981 Prob. F(2,15) 0.9754
Obs*R-squared 0.102911 Prob. Chi-Square(2) 0.9498
Source : A partir des données de
logiciel
Le Test de Breusch-Godfrey Serial Correlation LM Test effectuer
à travers le logiciel Eviwes (7),( annexe 4) nous fournisse un P-Vlaue
de 0.9498 >5%, par conséquent on accepte l'hypothèse nulle ,
les résidus ne sont pas autocorrélés .
2.3.2.2.3 Le test
d'hétéroscédasticité
La vérification de l'absence d'autocorrélation des
résidus doit être suivie par un test
d'hétéroscédasticité qui
étudie s'il existe une relation entre quelques variables et le terme
d'erreur . Nous utilisons le test de Breush-Pagan-Godfrey (annexe
5).
Hypothèses du test :
H0 :homoscédasticité
H1
:hétéroscédasticité
Règle de décision : accepter H0 si
p-value est supérieur à 5%
Tableau 13 : résultat du test
d'hétéroscédasticité

F-statistic 0.854323 Prob. F(12,18) 0.6013
Obs*R-squared 11.24910 Prob. Chi-Square(12) 0.5077
Source : A partir des données de
logiciel
Les résultats du test nous offrent un P-Value de
F-statisitc et un P-Value de Obs*R-Squared est supérieur à 5%.
Par conséquent nous acceptons l'hypothèse nulle donc notre
modèle est homosélastique.
Après avoir effectué ces différents test
, nous concluons que notre modèle est validé et significatif.
69
| 


