CHAPITRE VI :
ÉTUDE EXPLICATIVE DU STATUT SÉROLOGIQUE
SELON LES CARACTÉRISTIQUES DES FEMMES ENCEINTES
ENQUÊTÉES
Il
s'agit dans ce chapitre de ressortir les différents critères les
plus déterminants du statut sérologique en se servant d'un
modèle logit-linéaire. À travers la lecture des risques
relatifs sera dégagé le profil des femmes enceintes les plus
susceptibles d'avoir un statut sérologique positif.
VI.1. Justification du choix du modèle
L'analyse de la régression est une technique
statistique permettant d'établir une relation entre une variable dite
expliquée et des variables dites explicatives, afin d'en étudier
les associations et pouvoir faire des prévisions (TAFFE, 2004). La
nature de la variable à expliquer conditionne la méthode à
utiliser, la régression linéaire ne s'avérant plus
être appropriée lorsque la variable dépendante est
qualitative et catégorielle. Dans cette situation, il est
généralement fait recours à deux types de modèles :
le modèle logit et le modèle probit. Les données de la
présente étude qu'il faut mettre en relation sont de nature
qualitative. Le statut sérologique qui est expliqué est
donné par les modalités «positif' et
«négatif'' obtenues à travers les résultats
du test au VIH/SIDA. Il s'avère donc être une variable binaire
(présence [1], absence [0] de séropositivité), ce qui
permet de faire recours à la régression logistique binomiale.
VI.2. Présentation du modèle
Dans
une série de femmes enceintes dont l'âge varie entre 15 et 49 ans
révolus, est consignée la séropositivité ou non en
fonction des variables indépendantes. Pour une caractéristique X
donnée de la variable indépendante, la régression
logistique permet de calculer la probabilité d'observer Y
(séropositivité ou non de la femme enceinte
enquêtée). Elle permet de modéliser l'espérance
mathématique de   conditionnelle à conditionnelle à   en introduisant au préalable un codage quantitatif permettant de
représenter les différents attributs : en introduisant au préalable un codage quantitatif permettant de
représenter les différents attributs :
 
En
posant  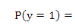 , la probabilité pour qu'une femme enceinte (vérifiant une
caractéristique , la probabilité pour qu'une femme enceinte (vérifiant une
caractéristique 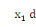  ) soit séropositive et ) soit séropositive et   , la probabilité pour qu'une autre femme enceinte
(vérifiant une caractéristique , la probabilité pour qu'une autre femme enceinte
(vérifiant une caractéristique   ) soit séronégative , le logit ë se
définit par exemple par la quantité ) soit séronégative , le logit ë se
définit par exemple par la quantité 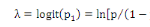 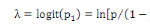 . Le modèle logit-linéaire se présente alors comme
suit : . Le modèle logit-linéaire se présente alors comme
suit :
 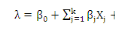 . .
Avec :
 ü ü 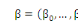 , le vecteur des paramètres du modèle ; , le vecteur des paramètres du modèle ;
 ü ü 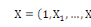 , une matrice où Xk est un facteur de
séropositivité auquel les femmes enceintes se trouvent
exposées ; , une matrice où Xk est un facteur de
séropositivité auquel les femmes enceintes se trouvent
exposées ;
ü
å est le vecteur des erreurs, qui suit une loi logistique (la fonction de
régression logistique s'écrivant   ). ).
| 


