I.7.3.1.a Modélisation de la source de chaleur
La modélisation de la source de chaleur est un point
clé de la simulation du soudage. La source de chaleur provenant du
soudage peut être introduite de différentes façons :
condition limite externe (terme d dans l'équation2) ou source interne de
chaleur (terme Qi dans l'équation 1). Dans tous les cas cette source est
fonction de l'espace et du temps dans le repère (0, X, Y, Z).
L'apport de chaleur peut être représenté
par une source interne de chaleur Qi (x, y, z) ou par une densité
surfacique de flux de chaleur q (x, y). Une source de chaleur en forme de deux
demi-ellipsoïdes a ainsi été proposée par Goldak pour
modéliser l'apport de chaleur associé aux procédés
de soudage avec apport de matière (figure I.8 a).
Pour modéliser le soudage à haute
énergie (faisceau d'électrons, laser) par
pénétration, une source volumique gaussienne à
décroissance linéaire dans l'épaisseur (figure
I.8.b) est recommandée. Pour modéliser
le soudage laser par conduction on peut utiliser une source gaussienne
surfacique (figure I.8. e).
Il faut cependant signaler que la modélisation de
l'apport de chaleur, même à l'aide de formes de source
prédéfinies, n'est jamais facile et nécessite souvent un
recalage sur des données expérimentales comme la ZAT
[15].

Chapitre I Recherches bibliographique.
28
Figure I.8 Modélisation de l'apport de
chaleur [15]
Chapitre I Recherches bibliographique.
29
Chapitre I Recherches bibliographique.
? Energie émise et énergie absorbée
[16]
Dans le cas du soudage à l'arc électrique,
l'énergie émise par unité de temps vaut :
(3)
En réalité, seule une fraction de cette
énergie sert effectivement à chauffer et faire fondre la
pièce, le reste étant échangé avec
l'extérieur par convection et rayonnement autour de la colonne d'arc et
du bain fondu. Etant donné que les phénomènes physiques
complexes présents dans l'arc et les mouvements de convection dans le
bain fondu ne sont pas modélisés, seul un paramètre de
« rendement », inférieur à 1, est incorporé
à la modélisation de l'apport de chaleur, de façon
à englober l'ensemble des pertes, selon la relation :
(4)
I.7.3.1.b Résolution de l'équation de chaleur
par la méthode des éléments finis
La résolution du problème thermique par
éléments finis permet, de prendre en compte les nombreuses non
linéarités qui interviennent dans l'équation de la chaleur
(propriétés thermophysiques dépendant de la
température, chaleur latente, échanges de chaleur avec le milieu
extérieur...). Cependant, une analyse tridimensionnelle transitoire
d'une opération de soudage complète nécessite encore des
temps de calcul et de capacités mémoires relativement importants.
C'est pourquoi certaines stratégies de résolution sont parfois
adoptées, qui consistent par exemple à réduire la
dimension du problème. Nous allons rappeler ces différentes
stratégies ci-dessous.
? Résolution du problème 3D complet
(transitoire)
On considère dans ce cas l'équation 1, qui
traduit le bilan thermique sur l'ensemble de la structure tridimensionnelle. Il
est alors nécessaire de définir le mouvement de la source de
chaleur sur ce domaine, comme une condition limite (ou bien une source interne
de chaleur) en mouvement sur le maillage. La résolution fait alors
intervenir une discrétisation temporelle, en plus d'une
discrétisation spatiale correspondant au maillage.
Dans le cas d'une analyse transitoire tridimensionnelle, les
gradients de températures (voire de microstructure dans le cas de
transformations de phases) très intenses au voisinage immédiat de
la source de chaleur doivent être représentés finement.
Cette source de chaleur
30
étant mobile, cela conduit à des maillages
tridimensionnels extrêmement denses. L'une des difficultés
rencontrée est alors de concilier un maillage qui soit suffisamment fin
autour de la source de chaleur, avec des temps de calcul et des
capacités mémoires qui restent du domaine du raisonnable dans un
contexte industriel.
Une méthode parfois utilisée pour palier aux
temps de calcul trop prohibitif est la technique du maillage adaptatif, qui
consiste à raffiner automatiquement le maillage autours de la source au
fur et à mesure de l'avancée de celle-ci, et à regrossir
le maillage après son passage. Il est alors nécessaire, pour
mettre en oeuvre cette méthode, d'assurer d'une part la
compatibilité des maillages au niveau du raffinement, et d'autre part de
disposer d'algorithmes de transport des grandeurs physiques entre deux
maillages.
C'est essentiellement au niveau mécanique que des
problèmes peuvent se poser : lorsque le maillage est
déplacé, l'état de contrainte résiduel est
réduit sur l'échelle grossière, ce qui entraîne une
certaine perte d'information.
En l'absence d'une telle technique, les principaux
inconvénients du calcul transitoire complet, bien qu'il s'agisse de la
simulation la plus réaliste, sont les temps de calcul et les
capacités mémoires trop importants, essentiellement si on
considère le calcul aval mécanique.
? Résolution du problème 3D en quasi
stationnaire
La résolution en quasi-stationnaire présente
l'avantage d'être rapide, tout en conservant un maillage tridimensionnel
avec une forte densité autour de la source. Aucune discrétisation
temporelle n'est effectuée, le problème étant
indépendant du temps.
Ce type de modélisation est souvent utilisé afin
d'ajuster la modélisation de la source de chaleur de façon
rapide. Il est en effet fréquent d'effectuer plusieurs calculs en
ajustant la source de chaleur defaçon à caler les
résultats numériques sur des résultats
expérimentaux (mesures de températures ou macrographie de la zone
fondue), en vue d'une analyse mécanique avale transitoire. Par
conséquent, le calcul quasi-stationnaire permet de caler un
modèle de source, qui est ensuite réinjecté dans une
simulation transitoire tridimensionnelle. Il est également possible de
compléter une simulation quasistationnaire par une analyse
transitoire.
Chapitre I Recherches bibliographique.
31
? Résolution 2D
Les simulations numériques transitoires
tridimensionnelles étant coûteuses en ressources informatiques,
des simulations bi-dimensionnelles sont parfois adoptées. Ce fût
notamment beaucoup le cas lors de l'émergence de la simulation du
soudage dans les années 1970, alors que les moyens informatiques de
l'époque ne permettaient pas de recourir à des simulations 3D.
Dans la majorité des cas, les simulations 2D
considèrent une section transverse, perpendiculaire à
l'avancée de la torche de soudage (fig.II.2. (a)). Des calculs 2D
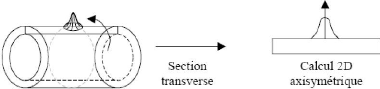
axisymétriques (fig.II.2 (b)) sont parfois également
adoptés pour le cas du soudage de conduites cylindriques, bien que dans
certains cas, une simulation 3D avec des éléments de coques soit
possible.
Le problème 2D est ainsi traité en
considérant une longueur unité dans la direction de soudage,
c'est-à-dire que la chaleur est déposée
simultanément sur les 1m (ou sur la circonférence de la conduite,
si le problème est traité en axisymétrique). L'apport de
chaleur est alors appliqué sur le maillage 2D en fonction du temps, de
façon à reproduire l'approche et l'éloignement de la
source.
Ce type de modélisation ne permet pas de
représenter le flux de chaleur dans la direction longitudinale
(perpendiculaire au plan de maillage), et il est en général
très difficile de reproduire une évolution réaliste des
températures dans ces conditions.
D'autres choix sont également possibles pour la section
à mailler : on peut choisir par exemple de mailler une section
longitudinale (cf. fig. 1.9.(d)), ou bien, si on considère que les
températures sont constantes dans l'épaisseur, on peut choisir de
mailler le plan moyen de la plaque (cf. fig. 1.9.(c))
Les simulations bidimensionnelles, malgré leurs
défauts, on permis de dégager un certain nombre de conclusions,
et demeurent fréquentes, notamment pour les simulations de soudage
multipasse. Dans tous les cas, les simulations 2D posent ensuite un certain
nombre de problèmes en ce qui concerne le calcul mécanique.
Chapitre I Recherches bibliographique.
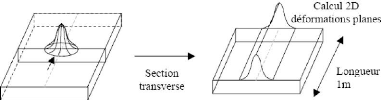
Figure 1.9. (a) : modélisation d'une
section transverse [16]
32
Figure 1.9. (b) : modélisation 2D
axisymétrique (cas d'une conduite cylindrique) [16]
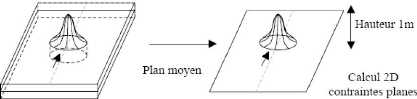
Figure 1.9. (c) : modélisation 2D du
plan moyen [16]
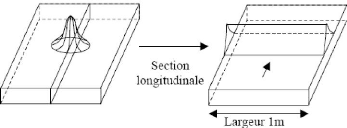
Figure 1.9. (d) : modélisation 2D d'une
section longitudinale [16]
Chapitre I Recherches bibliographique.
33
I.7.3.2 Modélisation des transformations
métallurgiques
| 


