II.
Présentation de la méthode DEA
La méthode DEA est fondée sur la programmation
linéaire et a pour objectif d'identifier des fonctions de production
empiriques. DEA compare toutes les unités similaires dans une population
donnée en prenant en compte simultanément plusieurs dimensions.
Chaque unité est considérée comme une
unité décisionnelle (Decision-making Unit - DMU) qui transforme
des inputs en outputs. Chaque DMU consomme ainsi un montant m
de différents inputs afin de produire s
différents outputs. La DMU (j) (j =1,...m) consomme un montant X {ij}
d'inputs (i = 1,...m) et produit un montant Y {rj} d'outputs (r = 1,...s).
La frontière efficiente est définie par le trait
en pointillé, à partir des coordonnées de chaque DMU : par
exemple le DM1 consomme un input unique X1 pour produire un output unique Y1.
Le problème revient alors à trouver quel sous-ensemble des n DMU
détermine la surface enveloppant le niveau de production efficiente
(figure).

Figure1 : Frontière de production non
paramétrique
Dans le cas général où l'on
considère de nombreux inputs et de nombreux outputs, la mesure
d'efficience productive (EP) se mesure par le ratio :
EP = (somme pondérée des outputs) / (somme
pondérée des inputs).
La frontière efficience sera constituée des
unités affichant des scores égaux à 1, pour les autres
DMU, il sera compris entre 0 et 1. La méthode peut être
envisagée selon deux approches légèrement
différentes : une approche orientée inputs et une approche
orientée outputs. La première optimise la consommation des inputs
pour un niveau d'outputs donné, la seconde maximise les outputs pour un
niveau constant des inputs. Les deux approches donnent des scores très
proches et un classement identique des firmes.
- Modèle CCR
La généralisation du programme DEA a
été développée au travers de l'approche CCR
(Charnes, Cooper, Rhodes, 1978 in Banker, Charnes et Cooper, 1984),
orienté inputs et à rendements d'échelle constants. Pour
chaque DMU k, la forme « ratio » de DEA revient à maximiser en
présence de r outputs et de i inputs,
le rapport hk tel que:
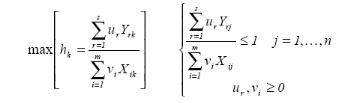
Avec,
k : le « benchmark » (firme dont on
mesure l'efficience) ;
hk : la forme « ratho » du
score d'efficience technique pour la firme k ;
Yrk : la quantité d'output r pour le
DMU k
ur : le coefficient de pondération de
l'output r ;
Xik : la quantité i pour le DMU
k ;
j : les DMU(s).
On peut reformuler le rapport hk de la
manière suivante:

Avec Ur le coefficient de pondération pour chaque
output r.
Au final, la forme duale s'écrit :

Avec,

- Modèle BBC
Le modèle BBC donne une surface enveloppe
linéaire par morceaux, avec des rendements d'échelle variables
(Banker, Charnes et Cooper, 1984). Le modèle BCC correspond au
modèle CCR avec l'ajout d'une contrainte de convexité :
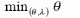
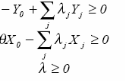
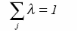
| 


