Environnements de grappes de calcul intensif sur réseaux d'entreprise: déploiement, exploitation et performances

Chapitre IV

EVALUATION DU MODELE SUR UNE

APPLICATION

Ce chapitre est la phase la plus pratique de notre travail. Il est constitué du déploiement de la grappe, de l'implémentation de l'ordonnancement d'un exemple sur cette grappe et du calcul des performances d'une réseau (latence, débit) d'une part et d'autre part de l'analyse des performances de l'application sur la grappe. Nous commencerons par présenter notre grappe, ensuite nous calculerons ses caractéristiques comme décrit dans le modèle, et par la fin nous analyserons les performances d'une application parallèle sur la grappe.

1 Présentation de l'architecture de notre grappe

Notre grappe est constituée de cinq stations de travail, reliées par un switch de 12 ports. La figure IV.1 l'illustre clairement. Pour le déploiement de notre grappe, des outils ont été installés à la base. - Nous avons installé un gestionnaire de tâches : OAR.

- le service NIS¹ : qui a pour rôle de distribuer les informations sur les utilisateurs et même sur les postes à travers toute la grappe. Ainsi, tout utilisateur ayant un compte sur le serveur NIS pourra se logger sur n'importe quelle machine de la grappe.

- Le service NFS² : On l'utilise en corrélation avec le serveur NIS pour distribuer le répertoire utilisateur sur les autres machines. Ainsi, tous les répertoires utilisateurs sur le serveur NFS seront accessibles sur n'importe quelle machine de la grappe.

- Le service SSH nécessaire pour se logger à distance.

- La bibliothèque de communications MPICH2 qui nous permettra de paralléliser les applications. L'installation de toutes ces composantes est précisée en annexe. Les caractéristiques des stations de travail sont récapitulées dans le tableau ci-dessous :

¹network information service ²network file system

Figure IV.1 - Notre grappe

	Processeur	Mémoire	Nom/adresse IP	SE
Machine1	Pentium 4, 3GHZ	512Mo	host1.labomaster/192.168.12.1	Debian 4.0
Machine2	Intel Celeron, 2GHZ	256Mo	host2.labomaster/192.168.12.2	Debian 4.0
Machine3	Pentium Dual @2GHZ	2Go	server.labomaster/192.168.12.3	Ubuntu 9.4
Machine4	Pentium 4,3.40GHZ	1Go	host3.labomaster/192.168.12.4	Debian 5.0
Machine5	Pentium 4,3GHZ	1Go	host4.labomaster/192.168.12.5	Debian 5.0

La machine 3 représente à la fois le serveur OAR, le serveur NIS, le serveur NFS et le serveur DNS. MPICH2 a été installé sur ce poste et est dupliqué via NFS sur les autres postes. Chacune de ces machines sont interconnectées par un réseau fast Ethernet 100Mbits/s. D'après notre modèle, une grappe hétérogène est modélisée par un graphe où les sommets sont les stations de travail caractérisées par la puissance du processeur, la mémoire et l'impact de la pile réseau. Dans le suite, nous décrirons comment nous avons estimé la troisième caractéristique.

2 Calcul des caractéristiques des noeuds du graphe de grappe

Lorsqu'une trame sort ou entre dans un hôte, elle traverse toutes les couches de la pile réseau et cela engendre un coût non négligeable.

2.1 Les surcoûts engendrés par la pile réseau relatifs à chaque station de travail

Il a été difficile de trouver un outil pour évaluer l'impact du protocole réseau; nous avons écrit un algorithme basé sur les sockets pouvoir évaluer les coûts engendrés par chaque ordinateur. Cet algorithme est basé sur le modèle client/serveur avec pour protocole UDP³ où le client envoie un message de 8 octets au serveur qui est déjà lançé. Ici le client et le serveur sont sur un même poste. Le code que nous avons écrit est le suivant.

CODE DU CLIENT

³User Datagram Protocol

#include <sys/types.h> #include <sys/socket.h> #include <netinet/in.h> #include <arpa/inet.h> #include <unistd.h> #include <stdio.h> #include <stdlib.h> #include <sys/un.h> #include<time.h>

int main (int argc, char* argv[]) {

struct timeval start,m;

struct sockaddr_in id; char s[3];

int id_socket,tempo,envoi,i=1,argument;

int erreur;

id_socket=socket(AF_INET,SOCK_DGRAM,0);

if (id_socket<0)

{perror("\nErreur dans la création du socket");

exit(1);

}

else

printf("\n socket : OK"); id.sin_family=AF_INET; id.sin_addr.s_addr=htonl(INADDR_ANY);

id.sin_port=htons(333); tempo=sizeof(id);

argument=atoi(argv[1]); while(i<=argument)

{

gettimeofday(&start,NULL); envoi=sendto(id_socket,&start,sizeof(start),0,(struct sockaddr*)&id,tempo);

i++;

sleep(1);

}

erreur=close(id_socket); exit(0);

return 0;

}

CODE DU SERVEUR

....

....

#define minim(a,b) ((a)<(b)?a:b)
#define maxim(a,b) ((a)>(b)?a:b)

int main (int argc, char* argv[]) {

id_de_la_socket=socket(AF_INET,SOCK_DGRAM,0);

if (id_de_la_socket<0)

{perror("\nErreur dans la création du socket");

exit(1);

}

else

printf("\n socket : OK"); is.sin_family=AF_INET; is.sin_addr.s_addr=htonl(INADDR_ANY);

is.sin_port=htons(333); tempo=sizeof(is);

erreur=bind(id_de_la_socket,(struct sockaddr*)&is,sizeof(is));

if (erreur<0)

{

perror("\nserver: bind\n"); exit(1);

}

else

printf("\nbind : OK\n"); printf("\n==NbrEnvoi=====MinRTT==================MaxRTT================MoyenneRTT\n"); max=0;

min=1000000;

argument=atoi(argv[1]); while(i<=argument)

{//printf("%d",i);

reception=recvfrom(id_de_la_socket,&start,sizeof(start),0,(struct sockaddr*)&is,&tempo); gettimeofday(&end,NULL);

res=(end.tv_sec-start.tv_sec)*1000000 + (end.tv_usec-start.tv_usec);

min=minim(min,res);

max=maxim(max,res);

moy=moy+res;

printf("Temps mis=%ld microsecondes \n",res);

i++;

}

printf("\n==%d===%d====%d===%1.f\n",(atoi(argv[1])),min,max,(moy/(atoi(argv[1])))); erreur=close(id_de_la_socket);

....

}

Le surcoût de la pile est considéré comme le temps mis par le message en local. Nous avons effectué l'envoi de 1.521.110 messages de 8 octets par machine à des moments différents. Après ces envois, nous avons recueilli les temps mis par le transfert en utilisant la fonction gettimeofdate et nous avons effectué la moyenne pour avoir une estimation fine.

2.2 Tableau récapitulatif et discussion

Nous obtenons donc la tableau ci-dessous qui regroupe tous les impacts correspondants aux différentes machines.

	Processeur	Mémoire	Coût induit par la pile(microsecondes)
Machine1	Pentium 4, 3GHZ	512Mo	23
Machine2	Intel Celeron, 2GHZ	256Mo	32
Machine3	Pentium Dual @2GHZ	2Go	5
Machine4	Pentium 4,3.40GHZ	1Go	31
Machine5	Pentium 4,3GHZ	1Go	12

On pourrait croire que l'impact du protocole réseau est proportionnel à la vitesse de traitement des processeurs mais la tableau nous présente le contraire. En effet, nous remarquons que les machines 1 et 5 ayant les mêmes vitesses de traitement induisent des coûts tout à fait différents. Celui de la machine 1 est à peu près le double de celui de la machine 5. D'autre part, la machine 4 ayant une vitesse d'exécution supérieure à celles des machines 1 et 5 induit un coût qui est presque la somme des coûts relatifs aux machines 1 et 2. Ceci nous amène à penser que les raisons plausibles sont liées aux activités du processeur au moment du calcul et à la gestion du protocole réseau par le système d'exploitation puisqu'on note que les systèmes d'exploitation sont différents. Le système d'exploitation aurait passer la main à un autre processus différent du notre pour un temps.

3 Calcul des caractéristiques des arcs du graphe de grappe

Pour évaluer les latences des liens, nous avons également écrit un programme basé sur les sockets tandis que pour évaluer les débits des liens nous avons utilisé des outils existants.

3.1 Evaluation des latences

Comme nous l'avons dit précédemment, nous avons écrit un programme sur le principe client/serveur basé sur les sockets en utilisant le protocole UDP mais cette fois on calcule le temps d'une requête réponse par le client c'est à dire que le client fait émet un message de 8 octets au serveur et attend la réponse de ce dernier. Il faut noter ici que le client et le serveur sont sur des postes différents. La latence est donc le temps requête/réponse UDP ou le RTT(Round trip time). Le code que nous avons fait est fourni ci-dessous :

Code du client

.... .... #define minim(a,b) ((a)<(b)?a:b)

#define maxim(a,b) ((a)>(b)?a:b)

....

int erreur;

int main (int argc, char* argv[])

{

....

⁴celui lancé pour exécuter le programme

....

int id_socket,tempo,envoi,i=1,reception;

id_socket=socket(AF_INET,SOCK_DGRAM,0);

if (id_socket<0)

{perror("\nErreur dans la création du socket\n");

exit(1);

}

else printf("\n socket : OK\n");

id.sin_family=AF_INET; id.sin_addr.s_addr=inet_addr("adresse_du_serveur");

id.sin_port=htons(3333); tempo=sizeof(id);

printf("\n==NbrEnvoi=====MinRTT======MaxRTT=====MoyenneRTT\n");

max=0;

min=100000;

argument=argv[1];

while(i<=argument)

{gettimeofday(&start,NULL); envoi=sendto(id_socket,&start,sizeof(start),0,(struct sockaddr*)&id,tempo); reception=recvfrom(id_socket,&end,sizeof(end),0,(struct sockaddr*)&id,&tempo); gettimeofday(&endl,NULL);

res=(endl.tv_sec-start.tv_sec)*1000000 + (endl.tv_usec-start.tv_usec); min=minim(min,res);

max=maxim(max,res);

moy=moy+res;

i++;

//sleep(3);

} printf("\n=====%d======%d====%d====%1.f\n",atoi(argv[1]),min,max,(moy/(atoi(argv[1])))); erreur=close(id_socket);

exit(0);

return 0;

Code du serveur

int main (int argc, char* argv[])

{

struct timeval end,start;

long int res;

int erreur,tempo,id_de_la_socket,reception,n,i=1,envoi; struct sockaddr_in is;

id_de_la_socket=socket(AF_INET,SOCK_DGRAM,0); if (id_de_la_socket<0)

{perror("\nErreur dans la création du socket\n"); exit(1);

}

else

printf("\n socket : OK\n");

is.sin_family=AF_INET;

is.sin_addr.s_addr=htonl(INADDR_ANY); is.sin_port=htons(3333);

tempo=sizeof(is);

erreur=bind(id_de_la_socket,(struct sockaddr*)&is,sizeof(is)); if (erreur<0)

{

perror("\nserver: bind\n");

exit(1);

}

else

printf("\nbind : OK\n");

//gettimeofday(&end,NULL);

argument = atoi(argv[1]);

while(i<=argument)

{

reception=recvfrom(id_de_la_socket,&start,sizeof(start),0,(struct sockaddr*)&is,&tempo); gettimeofday(&end,NULL);

envoi=sendto(id_de_la_socket,&end,sizeof(end),0,(struct sockaddr*)&is,tempo);

i++;

}

erreur=close(id_de_la_socket);

Nous avons effectué l'envoi de 1.521.110 messages de 8 octets par lien à des moments différents. Après chaque envoi, nous avons recueilli les temps mis par le transfert requête/réponse en utilisant la fonction gettimeofdate. Après tous les envois, nous avons effectué la moyenne de tous les résultats trouvés pour avoir une estimation fine. Nous avons obtenu les latences regroupées dans la tableau ci-dessous correspondantes aux liens entre les hôtes. Elles sont exprimées en microsecondes.

	Machine1	Machine2	Machine3	Machine4	Machine5
Machine1	x	272	107	127	125
Machine2	223	x	266	187	184
Machine3	123	255	x	260	91
Machine4	29	398	127	x	148
Machine5	126	355	100	132	x

La latence d'une machine M1 à une machine M2 n'est pas forcément la même de M2 à M1. Ceci est dû aux performances des processeurs qui sont différentes et au fait que les systèmes d'exploitation gèrent la pile réseau différemment. Il faut noter que le paquet arrive au niveau du commutateur qui étant donné son fonctionnement mettra un temps pour faire transiter le message.

3.2 Evaluation des débits des liens

Pour évaluer les débits des liens nous avons utilisé les outils netperf et iperf. Nous avons utilisé iperf pour confirmer les débits trouvés avec netperf. La syntaxe de la commande avec netperf est :

#netperf -H <adresse de la machine destinatrice> Le resultat est de la forme

Recv Send Send

Socket Socket Message Elapsed

Size Size Size Time Throughput

bytes bytes bytes secs. 10^6bits/sec

On a obtenu les résultats suivants en Mbits/s :

	Machine1	Machine2	Machine3	Machine4	Machine5
Machine1	x	94	87	94	83
Machine2	94	x	73	94	77
Machine3	65	81	x	90	94
Machine4	87	90	82	x	88
Machine5	86	82	94	82	x

3.2.1 Discussion

Le débit d'une machine M1 à une machine M2 n'est pas forcément le même de M2 à M1. Ceci peut être dû aux différences entre les vitesses de traitement des processeurs et aux charges des processeurs à un moment donné. Si un processeur est trop surchargé par rapport à l'autre, alors il y aura influence sur le débit. Par ailleurs, on voit que les 100 Mbits/s constituant le débit du réseau Fast-Ethernet n'est jamais atteint. On a en moyenne 85.85 Mbits/s. Cela peut être dû au fait qu'il y a des collisions sur le réseau entrainant ainsi des pertes de messages.

4 Programmation de l'application

Nous avons choisi de paralléliser la multiplication d'une matrice A par un vecteur V . 4.1 Algorithme

Le principe est le suivant : Le processus 0 est le processeur maître et détient la matrice et le vecteur. Les autres processus n'ont que le vecteur. Initialement le maître découpe la matrice et envoie une ligne de la matrice aux autres processeurs. Dès que le processeur termine d'exécuter la tâche qui est le produit d'une ligne reçue par le vecteur, il renvoie le résultat au maître. Le maître chaque va tester s'il y a encore une ligne non envoyée et si tel est le cas, il envoie à un processeur libre. Le code est le suivant :

4.2 Code

#define min(a,b) ((a)<(b)?a:b)

void initialiser(double m[SIZE][SIZE])

{

int i,j;

for(i=0;i<SIZE;i++) for(j=0;j<SIZE;j++) m[i][j]=1.0;

}

void maitre(int numprocs)

{

int i,j, sender,row,numsent=0; double a[SIZE][SIZE],c[SIZE]; double r;

MPI_Status status;

initialiser(a);

for(i=1;i<min(numprocs,SIZE);i++)

{

MPI_Send(a[i-1],SIZE,MPI_DOUBLE,i,i,MPI_COMM_WORLD);

numsent++;

}

for(i=0;i<SIZE;i++)

{

MPI_Recv(&r,1,MPI_DOUBLE,MPI_ANY_SOURCE,MPI_ANY_TAG,MPI_COMM_WORLD,&status); sender=status.MPI_SOURCE;

row= status.MPI_TAG-1;

c[row]=r;

if(numsent<SIZE){ MPI_Send(a[numsent],SIZE,MPI_DOUBLE,sender,numsent+1,MPI_COMM_WORLD);

numsent++;

} else

MPI_Send(MPI_BOTTOM,0,MPI_DOUBLE,sender,0,MPI_COMM_WORLD);

}

}

void esclave()

{

double b[SIZE], c[SIZE];

int i, row, myrank;

double r;

MPI_Status status;

for(i=0;i<SIZE;i++) b[i]=2.0;

MPI_Comm_rank(MPI_COMM_WORLD,&myrank);

if(myrank<=SIZE)

{

MPI_Recv(c,SIZE,MPI_DOUBLE,0,MPI_ANY_TAG,MPI_COMM_WORLD,&status); while(status.MPI_TAG>0)

{

row=status.MPI_TAG-1;

r=0.0;

for(i=0;i<SIZE;i++)

r+=c[i]*b[i];

MPI_Send(&r,1,MPI_DOUBLE,0,row+1,MPI_COMM_WORLD); MPI_Recv(c,SIZE,MPI_DOUBLE,0,MPI_ANY_TAG,MPI_COMM_WORLD,&status);

}

} } int main (int argc, char **argv){

int myrank,p;

MPI_Init (&argc, &argv);

MPI_Comm_rank (MPI_COMM_WORLD, &myrank);

MPI_Comm_size (MPI_COMM_WORLD, &p);

double startwtime = 0.0, endwtime;

char processor_name[MPI_MAX_PROCESSOR_NAME];

int namelen;

MPI_Get_processor_name(processor_name,&namelen);

fprintf(stdout,"Le Processus %d parmi %d est sur %s\n",myrank,p, processor_name); MPI_Barrier(MPI_COMM_WORLD);

if(myrank==0) {startwtime = MPI_Wtime();parent(p);}

else enfant();

MPI_Barrier(MPI_COMM_WORLD);

if(myrank==0)

{endwtime = MPI_Wtime();

printf("TEMPS DE CALCUL = %f\n", endwtime-startwtime);

}

...

Le code séquentiel du même problème est fournit en annexe. Pour calculer son temps d'exécution, il suffit de faire

#time ./executable

Nous avons utilisé MPICH2 pour réaliser cette application. Cependant l'ordonnancement que nous fait est fixée au départ et ne change pas tout au long de l'exécution.

5 Ordonnancement sur la grappe

L'ordonnancement est statique c'est à dire qu'il ne change pas tout au long de l'exécution de l'algorithme. Toutes les machines sont utilisées pour l'ordonnancement. La machine server est la machine sur laquelle s'exécute le premier processus. L'ordre d'ordonnancement est server - host2 - host3 - host4 - host1 : le premier processus s'exécute sur la machine server, le second sur la machine host2, le troisième sur la machine host3, le quatrième sur la host4 et le dernier sur la machine host1. S'il y

a encore des processus, alors on reprend avec la machine server et ainsi de suite. Exemple d'exécution avec 8 processus :

user@labofs:~/Desktop/codes$ mpdtrace // Pour avoir l'ordre d'ordonnancement

server

host2

host3

host4

host1

user@labofs:~/Desktop/codes$mpiexec -n 8 av Le Processus 0 parmi 8 est sur server

Le Processus 2 parmi 8 est sur host3 Le Processus 5 parmi 8 est sur server Le Processus 3 parmi 8 est sur host4 Le Processus 4 parmi 8 est sur host1 Le Processus 7 parmi 8 est sur host3 Le Processus 1 parmi 8 est sur host2 Le Processus 6 parmi 8 est sur host2 TEMPS DE CALCUL = 0.054822

5.1 Résultats et discussion

Nous avons obtenu les résultats suivants avec 5, 6, 8, 10, 12, 15, 20, 25, 30, 32, 40, 50, 100 processus.

Nous avons travaillé sur une matrice de tailles n=100, 1000, 3000, 5000 et 8000. Nous dénotons par T _par le temps parallèle, T_seq le temps séquentiel, Acc l'accélération et Eff l'efficacité.

Le temps de calcul séquentiel pour n=100, 1000, 3000, 5000 et 8000 sont respectivement 0.016 secondes, 0.042 secondes, 0.083 secondes, 0.092 secondes et 0.11 secondes sur la machine 3.

pour n=100 -*

Processus

		T_par(s)		Acc(T_seq/T_par)		Eff
5		0.69		0.02		0.004
6		0.06		0.26		0.04
8		0.05		0.32		0.04
10		0.07		0.22		0.02
12		0.08		0.20		0.01
15		0.09		0.17		0.01
20		0.14		0.11		0.005
25		0.19		0.08		0.003
30		0.3		0.05		0.001
32		0.36		0.04		0.001
40		0.55		0.029		0.0007
50		1.06		0.01		0.0003
100		6.1		0.02		0.00002

pour n=1000 -*

Processus

	T_par(s)	Acc(T_seq/T_par)	Eff
5	0.006	7	1.14
6	0.007	6	1
8	0.008	5.25	0.65
10	0.009	4.66	0.46
12	0.0095	4.42	0.36
15	0.0072	5.83	0.38
20	0.0075	5.6	0.28
25	0.3	0.14	0.0056
30	0.42	0.1	0.0033
32	0.5	0.084	0.0026
40	1.1	0.038	0.0009
50	2.4	0.017	0.00035
100	6.29	0.0066	0.00006

pour n=3000 -*

Processus

	T_par(s)	Acc(T_seq/T_par)	Eff
5	0.004	20.75	4.15
6	0.003	27.66	4.61
8	0.0032	25.93	3.24
10	0.002	41.5	4.15
12	0.0021	39.52	3.29
15	0.0023	36.08	2.40
20	0.0025	33.2	1.66
25	0.003	27.06	1.10
30	0.3	0.27	0.009
32	0.47	0.17	0.005
40	0.7	0.11	0.002
50	2.04	0.040	0.0008
100	3.5	0.023	0.0002

pour n=5000 -*

Processus

		T_par(s)		Acc(T_seq/T_par)		Eff
5		0.0033		27.8		5.57
6		0.0034		27.05		4.50
8		0.0036		25.5		3.19
10		0.0038		24.21		2.42
12		0.0027		34.07		2.83
15		0.002		46		3.06
20		0.0024		38.33		1.91
25		0.0038		24.21		0.96
30		0.47		0.195		0.006
32		0.473		0.194		0.006
40		0.5		0.184		0.0046
50		3.04		0.030		0.0006
100		5.5		0.016		0.0001

n=8000 -?

Processus

	T_par(s)	Acc(T_seq/T_par)	Eff
5	0.0036	30.55	6.11
6	0.0037	29.41	4.90
8	0.0038	28.94	3.61
10	0.004	27.5	2.75
12	0.0017	64.70	5.39
15	0.0022	50	3.33
20	0.0024	45.83	2.29
25	0.0038	28.94	1.15
30	0.47	0.23	0.007
32	0.77	0.14	0.004
40	0.6	0.18	0.004
50	4.02	0.027	0.0005
100	7.9	0.013	0.0001

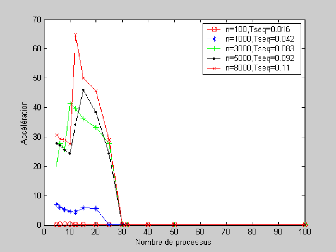
Figure IV.2 - Courbe représentant l'accélération de l'algorithme parallèle

Nous remarquons qu'avec une matrice de taille 100, l'accélération est presque nulle; cela veut dire que l'algorithme parallèle est inutile puisque le temps d'exécution en parallèle est plus grand que le temps séquentiel. Avec une matrice de taille 1000, on constate une amélioration des performances avec des processus allant de 5 à 20 processus. Et on trouve que l'algorithme est efficace avec 5 et 6 processus. Lorsqu'on passe aux tailles 2000, 3000, 8000, on remarque que l'algorithme est plus efficace lorsqu'on parallélise avec 20 ou 25 processus. Aussi, l'algorithme accélère avec 5, 6, 8, 10, 12, 15, 20, 25 processus bien qu'elle ne fournit pas une bonne efficacité dans ces cas. Lorsqu'on excède 25 processus, l'accélération et l'efficacité se dégradent rapidement jusqu'à zéro. En effet, le temps de calcul parallèle est alors considérablement réduit lorsque le nombre de processus augmente ceci les processus passent plus de temps à communiquer qu'à calculer.

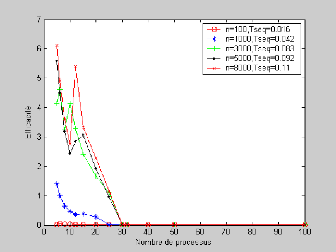
Figure IV.3 - Courbe représentant l'efficacité de l'algorithme parallèle