|
8 décembre 2009
Dédicaces
A ma chère grand-mère MEGNE Anne
A la mémoire de mon grand-frère Guy Bertrand
A mes parents et mes frères et soeurs : Marie Laure,
Irène Flore, Léontine Grâce,
Edith Florence, Francklin et Anicet
Remerciements
Je tiens tout d'abord à remercier Dieu Tout Puissant pour
l'intelligence et la santé qu'Il m'a accordées durant
l'accomplissement de ce travail.
Ce travail n'aurait vu le jour sans la présence d'une
grande femme en l'occurrence ma très chère Maman MEKA Madeleine,
qui, de part son courage et son endurance a toujours su, me soutenir durant
toutes les épreuves que j'ai dû traverser durant mon
éducation scolaire et sociale. Je saisis donc l'opportunité pour
lui témoigner une fois de plus toute ma reconnaissance et ma gratitude,
merci Maman.
Je remercie très profondément le Dr. Annie
Sylvie BEYA WAKATA, qui malgrè son planning chargé, a
accepté de diriger ce mémoire en répondant toujours avec
promptitude à mes sollicitations, tant de nature scientifique que
administrative mais aussi pour sa disponibilité, son optimisme et son
enthousiasme. Qu'elle trouve ici, l'expression de ma profonde gratitude.
Je remercie vivement tous les enseignants du
Département de Physique de la Faculté des Sciences de
l'Université de Yaoundé I pour tous les enseignements
dispensés depuis la première année. Je pense
particulièrement aux : Prof. DOMNGANG Samuel, Prof. MANGUELLE
Eliézer, Dr. MAGA Emire, Dr. TCHOFFO Fidèle, Dr. HDR NDJAKA
Jean-Marie, Dr. ZEKENG Serge, Dr. MBIANDA Gilbert, Dr. WAKATA Annie, Dr NDOP
Joseph, Dr. EDONGUE Hervais.
Je remercie tout particulièrement Max et ESSAKA Fritz
pour m'avoir accordé du temps et pour m'avoir plongé dans le bain
de la programmation sans m'y noyer. Leur aide m'a été
également précieuse dans la compréhension des
résultats qu'affichait le programme.
Je remercie les familles WEMBE, SIDZE, FOTSO, FONGUIENG,
KUETCHE, TAGNE, PONE pour leur soutien moral et financier. Je pense aussi
à tout ceux qui m'ont supporté, d'une manière ou d'une
autre, dans la vie de tous les jours et qui m'ont, mine de rien, grandement
facilité la tâche.
Mes remerciements vont également à l'ensemble de
mes chers (es) amis (es), NJOUONANG Herman,
NOUTCHIO Liliane, TCHOUAFA Jean Bonheur, NGUENANG Christian,
TAMBA Gaston, WONSO Arnaud, NANA Landry, KOMGUEP Guy, NGAMI Patiente, TAMGHO
Anicet, KEPCHE Stéphanie, TANGNING Blériand, FEUBI Patrick,
LAPEMEU Nadège, NZEUHANG Rodrigue, TCHAPDA Collinet, TCHIO Martial, YAMO
Dallyl, LEBONGO Achille, NGANKIO Guy avec qui j'ai partagé des moments
de joie et des discussions diverses m'aidant à déstresser.
Je remercie tous mes camarades de promotion, TANKIO Roussel,
TUEKAM Enselme, NGONGANG Rickielle, TCHIAZE Igor, ZAMBOU Serges, NOUDJIO
Martial, DONGHO Moïse, KAMTA Marcel, SIMO Aline et DJINKWI Martial pour la
bonne ambiance qu'ils ont su créer au sein du laboratoire et pour leurs
discussions intéressantes.
Et enfin, un grand merci à toute ma famille, et plus
particulièrement à ma grande soeur, Marie Laure, pour m'avoir
toujours soutenu financièrement, moralement et encouragé. Merci
pour tout.
Que tout ceux qui ont contribué directement ou
indirectement à l'élaboration de ce travail et qui pensent que
leur noms auraient du figurer dans cette rubrique retrouvent ici toute ma
gratitude.
Resumé
Récemment, des études sur les mécanismes
de croissance des nano-cavités dans les semi-conducteurs
implantés d'ions ont été faites (expérimentalement
et numériquement). Ce document met en exergue le calcul numérique
du grossissement de ces nano-cavités par les deux potentiels
mécanismes de base : l'Oswald Ripening (maturation d'oswald) et la
Migration Coalescence. A des températures de recuit appropriées,
les résultats des calculs effectués sont peu différents
des résultats expérimentaux, du moins au niveau de l'allure des
courbes et nous observons l'effet de croissance. Il est important de
décrire les mécanismes de croissance dominants, afin de
déterminer et de contrôler les effets des nano-cavités dans
la fabrication des composants à base de semi-conducteurs. Ces travaux
permettront également de choisir les paramètres d'implantation
ionique appropriés aux performances et exigences requises pour la
fabrication de certains types de composants électroniques.
Abstract
Recently, discussions on the growth mechanisms of the cavities
in ions implanted semi-conductors were done (experimentally and
numerically).This document highlights the numerical calculation of the
magnification of these nano-cavities by two potential basic mechanisms : the
Oswald Ripening and Coalescence Migration. At the appropriate annealing
temperatures, numerical results are slightly different from experimental
results, at least at the speed curves and observe the effect of growth. It is
important to describe the dominant growth mechanisms to determine and monitor
the effects of nano-cavities in the manufacture of components based on
semiconductors. This work will also make possible to choose the appropriate
parameters of ion implantation and appropriate performance requirements for the
manufacture of electronic components.
Table des figures
|
1.1
|
Schéma d'un implanteur par faisceau d'ions [2]
|
10
|
|
1.2
|
Profils d'implantation du Bore dans le silicium [2]
|
11
|
|
1.3
|
Distribution des ions et des défauts en fonction de la
profondeur dans un matériau [3] . .
|
12
|
|
1.4
|
Mécanisme de freinage d'un ion dans un solide [3]
|
13
|
|
1.5
|
Schéma simplifié d'un implanteur plasma
|
15
|
|
1.6
|
boucle de dislocations formées dans le matériau.
[5]
|
19
|
|
1.7
|
Image en haute résolution d'une cavité
sphérique.[5]
|
20
|
|
1.8
|
Exemple de cavités facettées ou non obtenues pour
une implantation à 1,55 MeV de 5.1016
|
|
|
He/cm-2 et un recuit de 700°C pendant une heure.
[5]
|
21
|
|
2.1
|
Etapes du procédé Smart Cut.
|
24
|
|
2.2
|
Processus de piégeage (gettering).
|
25
|
|
3.1
|
Croissance thermique de nano-cavités, cas d'implantation
de l'As [E. Ntsoenzok].
|
29
|
|
3.2
|
Processus de migration coalescence.
|
30
|
|
3.3
|
Processus d'oswald ripening
|
31
|
|
3.4
|
Croissance de nano-cavités suivant le mécanisme
d'Oswald ripening
|
33
|
|
3.5
|
Représentation des invariances du rayon moyen des
nano-cavités/bulles en fonction de la
|
|
|
concentration d'hélium pour les différents
mécanismes de croissance, MC et OR
|
34
|
|
3.6
|
Schéma représentatif du phénomène de
coalescence entre deux nano-cavités
|
38
|
|
3.7
|
(a))Résultats des simulations de OR pour un recuit de
1800 s en fonction de la température
pour dt = 0,0001s;
(b))Résultats des simulations de OR pour un recuit de 1800 s en
fonction
|
|
|
de la température pour dt = 0,001s.
|
40
|
|
3.8
|
Influence du nombre de particules
|
40
|
|
3.9
|
(a))Simulations de OR pour un recuit de 1800 s en fonction de
la température pour 500
nano-cavités; (b))Résultats des
simulations de OR par J. H. Evans pour un recuit de 1800
|
|
|
s en fonction de la température et comparaison avec deux
résultats expérimentaux
|
41
|
3.10 (a))Histogramme de la distribution initiale de taille des
nano-cavités/bulles pour un recuit à 1050°C; (b))Histogramme
de la distribution de taille des nano-cavités/bulles pendant le recuit
à 1050°C après 1800 s. 41
3.11 Histogramme de la distribution ((a) initiale; (b) finale) de
taille des nano-cavités/bulles pendant un recuit à 1050°C
par J. H. Evans 42
3.12 (a)) : Graphe du rayon cubique en fonction du temps pour
calculs effectués à 1100°C et 1200°C; (b)) : Graphe du
rayon cubique en fonction du temps pour calculs effectués à
1100°C et 1200°C par J. H. Evans. 43
Table des matières
Dédicaces i
Remerciements ii
Résumé iv
Abstract 1
Liste des figures 3
Table des matières 5
INTRODUCTION GENERALE 6
1 IMPLANTATION IONIQUE ET FORMATION DES NANO-CAVITES 9
1.1 L'IMPLANTATION IONIQUE PAR FAISCEAU D'IONS 9
1.1.1 Définition 9
1.1.2 Principe 9
1.1.3 Mécanismes physiques liés à
l'implantation ionique 11
1.2 L'IMPLANTATION IONIQUE PAR IMMERSION PLASMA 14
1.2.1 Principe de fonctionnement 14
1.2.2 Avantages et Inconvénients 15
1.3 APPLICATIONS DE L'IMPLANTATION IONIQUE 16
1.4 RECUIT POST-IMPLANTATION 17
1.5 FORMATION DES NANO-CAVITES 18
1.5.1 Précurseurs 18
1.5.2 Création des nano-cavités 18
1.6 CONCLUSION DU CHAPITRE 21
2 APPLICATIONS POTENTIELLES DES NANO-CAVITES 22
2.1 PROCEDE SMART CUT 23
2.2 GETTERING (PIEGEAGE D'IMPURETES) 25
2.2.1 Les différentes méthodes de piégeage
26
2.3 CONCLUSION DU CHAPITRE 27
3 CROISSANCE DES NANO-CAVITES/BULLES 29
3.1 CROISSANCE THERMIQUE DES NANO-CAVITES 29
3.1.1 La Migration Coalescence 29
3.1.2 L'Oswald Ripening (Maturation d'Oswald) 31
3.1.3 Comparaison des deux mécanismes de croissance
33
3.2 INTERET DE L'ETUDE DES NANO-CAVITES/BULLES 34
3.3 SIMULATIONS NUMERIQUES 35
3.3.1 Modèle de croissance par Oswald Ripening 35
3.3.2 Modèle de croissance par Migration Coalescence
37
3.3.3 Résultats de simulations et Discussions 39
CONCLUSION GENERALE 44
ANNEXE 46
Bibliographie 48
INTRODUCTION GENERALE
En raison du développement de l'industrie, du transport
et des moyens de communication, une croissance de la consommation mondiale
d'énergie a été observée pendant les
dernières décennies. Les besoins en énergie vont de plus
en plus augmenter dans le monde et les enjeux dans ce domaine deviendront de
plus en plus cruciaux. Cette forte augmentation des besoins en énergie
s'accompagnera d'une baisse globale des réserves
pétrolières et des efforts visant à réduire le
réchauffement climatique. Deux ressources d'énergie naturelles
apparaissent comme sources alternatives : l'énergie éolienne et
l'énergie solaire. Cette dernière est la source d'énergie
la plus prometteuse et la plus puissante. Avec environ 125 000 000 milliards de
watts de puissance solaire frappant la terre à n'importe quel moment,
l'énergie solaire devrait logiquement être la source
d'énergie renouvelable de demain. Les panneaux (panneaux
photovoltaïques) solaires sont destinés à
récupérer une partie du rayonnement solaire pour la convertir en
énergie électrique par le biais des cellules solaires
constituées de matériaux semi-conducteurs sous forme de couches
minces (silicium, sulfure de cadmium, tellure de cadmium, etc.) qui peuvent
libérer leurs électrons. De plus le silicium représente
90% de la production du photovoltaïque. Le matériau est
généralement pollué par des impuretés
métalliques et doit être purifié pour améliorer la
durée de vie des porteurs et par conséquent le rendement des
cellules solaires. D'autre part, les besoins de plus en plus importants en
silicium et par conséquent le déficit de ce dernier (le manque de
silicium a freiné la croissance du photovoltaïque en 2005 et 2006)
amène à explorer d'autres sources notamment du silicium dit
'sale' ou silicium métallurgique. Avec dans ce dernier cas un besoin
encore plus vital de purification par neutralisation des impuretés
métalliques afin de former des cellules solaires de bonne
qualité, qui permettront de réaliser des structures
photovoltaïques perfomantes à bas coûts. La réduction
significative des coûts viendra plus sûrement de la fabrication et
l'utilisation des couches minces permettant une augmentation
considérable des rendements.
Les enjeux actuels de l'industrie du semi-conducteur concernent
la réduction de la taille des dispositifs et la diminution des
coûts de production, tout en améliorant les performances et les
fonctionnalités. Par ailleurs, le développement
rapide de l'industrie électronique intervenu pendant ces
dernières années requiert de nouvelles méthodes de
croissance et de modification des propriétés des matériaux
semi-conducteurs. Récemment, l'inclusion des nanostructures dans les
matériaux (principalement le silicium), lors des processus
d'élaboration a été envisagée. La
compréhension du mécanisme de croissance des nano-cavités
créées par cette inclusion est donc déterminante pour le
développement de nouvelles méthodes de fabrication des
matériaux (à faible coût), et pourrait faire baisser de
manière considérable le prix du kWh de l'énergie
électrique provenant du solaire (209,6 Frs CFA/kWh [23]) par rapport
à celle provenant de l'hydroélectrique (AES-Sonel) qui est de 70
Frs CFA /kWh.
En raison des limitations expérimentales et
théoriques, les simulations apparaissent comme alternatives pour
étudier de tels processus au sein du laboratoire des sciences des
matériaux (L.S.M) du Département de Physique de la Faculté
des Sciences de l'Université de Yaoundé 1. En effet, les
expériences fournissent des informations importantes sur la croissance
des nano-cavités et leur environnement. Cependant, la résolution
spatio-temporelle des dispositifs expérimentaux ne permet pas
l'observation de la cinétique, encore moins la compréhension des
processus au niveau microscopique.
Dans ce mémoire, l'objectif est de présenter
dans un premier temps, la méthode de fabrication de couches minces de
matériaux semi-conducteurs par implantation ionique et, la purification
de films minces au moyen des nano-cavités induites par implantation
ionique (le gettering). Dans un second temps, l'étude théorique
et numérique de la croissance de ces nano-cavités (selon les deux
mécanismes, oswald ripening et migration coalescence) sera menée
car la connaissance de leur taille nous permet de déterminer et de
contrôler les propriétés des matériaux. Ce manuscrit
se présente comme suit :
- Dans le chapitre 1, nous décrivons
premièrement l'implantation ionique par faisceau d'ions et
l'implantation ionique par immersion plasma, ensuite la compréhension de
la formation des nano-cavités induites est abordée. L'interaction
de l'ion implanté (hydrogène et/ou hélium) avec les
défauts, la migration et la formation des complexes et des
nano-cavités seront également mises en exergue.
Le chapitre 2 concerne l'une des techniques de production des
couches minces oil nous verrons l'importance directe des cavités/bulles,
et une méthode de purification de ces couches, qui sont des applications
potentielles de nano-cavités.
- Enfin, l'étude menée au chapitre 1 sur les
différents phénomènes qui forment les
précurseurs
qui à leur tour donneront obligatoirement des
cavités/bulles, nous permettra d'aborder au chapitre 3, la croissance de
ces cavités.
En nous appuyant sur des modèles (comme celui de J. H.
Evans [1]) de croissance thermique, nous avons rédigé un code de
simulation dans le langage de programmation C++ permettant de faire des
perspectives d'évolution de la tailles des cavités 1
en fonction de la température et du temps de recuit et les calculs sont
comparés aux résultats existants.
1. L'emploi des deux termes cavités ou nano-cavités
sera confondu.
CHAPITRE PREMIER
IMPLANTATION IONIQUE ET
FORMATION DES NANO-CAVITES
1.1 L'IMPLANTATION IONIQUE PAR FAISCEAU D'IONS
L'implantation ionique est utilisée depuis longtemps
dans l'industrie électronique. L'idée est de Schockley (un des
inventeurs du transistor) qui proposa l'implantation ionique pour le dopage des
semi-conducteurs dès 1951. A partir de 1971, le procédé
fut industrialisé pour la fabrication des circuits
intégrés. Proposé dès 1973 pour des applications
mécaniques, il fut rapidement utilisé avec succès. Des
applications ont vu le jour dans l'industrie mécanique,
aéronautique, biomédicale.
1.1.1 Définition
L'implantation ionique par faisceau d'ions est un
procédé d'ingénierie des matériaux. Comme son nom
l'indique elle consiste à modifier les propriétés d'un
matériau par l'insertion d'ions dans son volume. Il existe deux
processus d'implantation ionique : implantation par faisceau d'ions et
implantation par immersion plasma.
L'implantation ionique est également utilisée
dans l'industrie électronique pour la fabrication de certains composants
semi-conducteurs (microélectronique) et pour le traitement de la surface
des métaux. Les ions permettent à la fois de changer les
propriétés chimiques de la cible, mais également les
propriétés structurelles car la structure de la cible peut
être abîmée ou même détruite.
1.1.2 Principe
A partir d'une source gazeuse, solide ou liquide, contenant
l'atome à implanter, un plasma est créé 1. Un
champ électrique appliqué à la sortie de cette source
permet l'extraction des ions. Ce faisceau ionique traverse ensuite un champ
magnétique oil l'on sélectionne l'ion à implanter en
1. les ions que l'on souhaite implanter sont tout d'abord produit
à partir d'un gaz, qui est ionisé par bombardement
électronique.
fonction de sa masse atomique. Le faisceau est ensuite
accéléré, puis focalisé sur toute la surface de
l'échantillon.
La quantité de matériaux implantée,
appelée dose ou fluence est l'intégrale sur le temps du courant
ionique. Les courants électriques en jeu dans les implanteurs sont de
l'ordre du microampère. Ils ne permettent donc d'implanter qu'une faible
quantité d'ions. Cette technique n'est utilisée que dans les
domaines oil la modification recherchée est faible.
L'accélération des ions atteint typiquement des énergies
allant de 10 à 500 keV. Toutefois, il est possible de se limiter
à des énergies inférieures à 10 keV, mais dans ce
cas la pénétration ne dépasse jamais quelques
nanomètres. On trouve également des accélérateurs
qui sont capables d'accélérer des ions jusqu'à 5 MeV, mais
cela provoque des dégâts structurels importants de la cible. Par
ailleurs, étant donné que la distribution de la profondeur de
pénétration est large, le changement de composition en un point
donné est relativement faible car les profils de composition ne sont pas
toujours des gaussiennes parfaites : il peut y avoir une légère
déformation (ou asymétrie, kurtosis en anglais) rendant le profil
asymétrique (figure 1.2). Ces profils sont généralement
calculés avec le logiciel TRIM (Transport Range IMplantation), il nous
donne une idée de la distribution en profondeur des ions dans le
matériau.
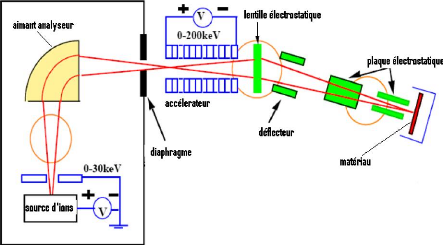
FIGURE 1.1: Schéma d'un implanteur par faisceau d'ions
[2]
Les ions dopants sont vaporisés, projetés sur le
matériau cible (porté à une certaine température)
dans lequel se produisent de nombreuses collisions. Ces ions subissent alors
une perte graduelle d'énergie, jusqu'à ce qu'ils s'arrêtent
à une profondeur. Ce traitement, qui utilise des faisceaux d'ions de
haute énergie, permet une profondeur moyenne de
pénétration des atomes allant de
100 Aÿ à 1 um. La profondeur moyenne
est contrôlée en ajustant l'énergie
d'accélération, et la dose d'impuretés implantées
est fixée par le courant ionique et la durée du balayage. Le
principal effet secondaire est la création des défauts ponctuels
ou étendus dans le matériau, dus principalement aux collisions
nucléaires. Afin d'éliminer ces défauts et aussi d'activer
les dopants par diffusion de ceux-ci en sites substitutionnels, un traitement
thermique (recuit) est ensuite nécessaire.

FIGURE 1.2: Profils d'implantation du Bore dans le silicium
[2]
1.1.3 Mécanismes physiques liés à
l'implantation ionique
Nous allons décrire dans ce paragraphe quelques
mécanismes mis en jeu au cours d'une implantation ionique. En effet en
pénétrant dans le solide, les ions perdent leur énergie
selon deux processus, comme le montre la figure 1.3 :
- Le freinage électronique, au cours duquel
l'énergie est transmise aux électrons; - Le freinage
nucléaire, dans lequel le transfert se fait aux atomes du solide.
a) Collision atomique
Au cours d'une implantation ionique, une longue
séquence de collisions atomiques successives est observée. Un
phénomène important lié à l'implantation ionique
est la formation de défauts. En effet, lors du freinage
nucléaire, l'ion incident peut transférer des quantités de
mouvement importantes aux atomes du réseau. Si l'énergie
transmise est supérieure à une valeur seuil Ed, appelée
énergie de déplacement, un atome va être
déplacé et mis en position interstitielle, laissant un site
vacant (lacune). Ce couple de défauts composé d'un interstitiel
et d'une lacune est appelé paire de Frenkel. C'est le défaut le
plus simple créé par implantation. La distribution de
défauts

FIGURE 1.3: Distribution des ions et des défauts en
fonction de la profondeur dans un matériau [3]
est aussi généralement de type gaussien et est
centrée de part et d'autre d'une profondeur Rd, oil le pouvoir
d'arrêt nucléaire est maximal. La profondeur d'arrêt des
ions Rp est elle plus grande que la profondeur Rd. La figure 1.3
représente la concentration d'ions (impuretés) et de
défauts en fonction de la profondeur dans un matériau.
Dans les deux processus, l'évènement
élémentaire est la collision binaire ion-atome et il s'agit d'une
interaction coulombienne. En règle générale, ces deux
processus de freinage sont indépendants et peuvent s'ajouter, mais
souvent l'un des deux est négligeable. En effet, leurs sections
efficaces varient différemment selon l'énergie des ions incidents
: elle est maximale à haute énergie (environ 1 MeV) pour le
freinage électronique, et à faible énergie (de l'ordre du
keV) pour le freinage nucléaire[3].
b) Amorphisation, Diffusion, Pulvérisation
L'amorphisation qui est le fait de rendre une substance
amorphe, généralement par bombardement ionique, conduit à
une perte totale de la périodicité de la structure cristalline.
Elle a lieu lorsque la densité maximale de défauts que l'on peut
atteindre dans un matériau est égale à la densité
atomique de ce dernier (par exemple lorsque la densité de défauts
est de 4, 97.102 pour le silicium).
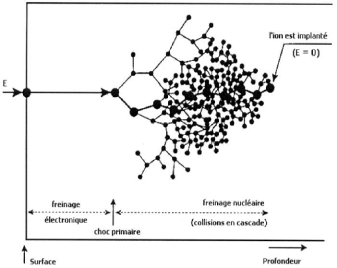
FIGURE 1.4: Mécanisme de freinage d'un ion dans un
solide [3]
De plus, ce phénomène d'amorphisation
dépend de la température d'implantation. En effet, pour des
températures élevées, la diffusion des défauts
(interstitiels et lacunes isolées) est possible et il faut alors des
doses élevées pour atteindre l'amorphisation. Inversement,
à faible température la diffusion est faible et l'amorphisation
est plus facilement atteinte.
Il existe ainsi pour chaque matériau une
température d'implantation critique, qui dépend de
l'espèce ionique implantée, au delà de laquelle il est
impossible de créer une couche amorphe.
Un phénomène supplémentaire vient
s'ajouter à cela : au cours de l'implantation, la température du
matériau augmente, ce qui peut entrainer une diffusion notable de
l'impureté (l'ion) implantée, mais également une
redistribution des impuretés déjà présentes dans le
matériau.
Un autre effet de l'implantation dont on doit tenir compte est
la pulvérisation de la surface bombardée, qui peut être
importante si la dose des ions implantés est élevée et
l'énergie faible. Ce phénomène est aussi observé
lors d'une implantation d'ions suffisamment énergétiques ou
lourds (la masse atomique plus grande que celle des atomes du substrat); ces
ions peuvent alors arracher
des atomes à la surface. On parle ainsi d'une
pulvérisation de surface. L'émission ne concerne pas
exclusivement les atomes du matériau cible, cela peut aussi se traduire
par la rétrodiffusion d'ions incidents, de photons ou encore
d'électrons.
L'implantation ionique présente un attrait particulier car
elle permet de contrôler divers paramètres avec précision
:
- La profondeur moyenne de l'espèce implantée par
rapport à la surface en ajustant l'énergie
d'accélération des ions.
- La quantité de l'espèce introduite en agissant
sur le courant ionique et la durée d'exposition au faisceau.
- Le profil de l'espèce implantée en effectuant des
implantations multiples à différentes énergies.
1.2 L'IMPLANTATION IONIQUE PAR IMMERSION PLASMA
Pour contourner les limitations et la complexité de la
manipulation des faisceaux d'ions, une autre technique de production et
d'accélération d'ions a vu le jour. C'est l'implantation ionique
par immersion plasma. Cette technique est fréquemment utilisée
dans le secteur de la microélectronique pour le dopage de
semi-conducteurs.
1.2.1 Principe de fonctionnement
L'implantation ionique par immersion plasma est aussi un
procédé d'ingénierie des matériaux. Comme son nom
l'indique elle consiste à plonger la pièce à traiter
(substrat) au sein du plasma et à lui appliquer des impulsions
négatives haute tension. Ces impulsions vont contribuer à la
formation d'une gaine ionique autour du substrat. En effet, les
électrons étant beaucoup plus légers que les ions, leur
flux est d'autant plus important. Au voisinage du substrat polarisé
négativement, le plasma a donc tendance à s'appauvrir en
électrons et à se charger positivement, ce qui contribue à
la formation d'une gaine ionique autour du substrat (figure 1.5).
Accélérés par la polarisation négative, les ions
positifs sont attirés par la gaine et finissent par s'implanter dans le
matériau.
Comme le plasma entoure le substrat, toute la surface est
implantée en même temps ce qui permet aussi de supprimer
l'étape de balayage du faisceau d'ions.
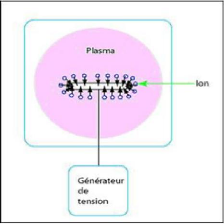
FIGURE 1.5: Schéma simplifié d'un implanteur
plasma
1.2.2 Avantages et Inconvénients
L'avantage de l'implantation ionique par immersion plasma est
que les ions positifs s'implantent simultanément sur toute la surface du
matériau et sont ainsi répartis uniformément. De plus, ce
procédé peut être réalisé à basse
température, ce qui permet d'éviter les éventuels dommages
que pourrait causer la chaleur.
Entre autres, voici donc quelques avantages
supplémentaires :
- Le procédé permet aussi de traiter facilement des
pièces à géométrie complexe. La taille des
pièces ne détermine pas le temps de traitement.
- Les pulses très courtes empêchent la
pièce de chauffer; permettant d'avoir une température de
traitement peu élevée.
- L'implantation ionique ne permet pas de créer des
couches très épaisses, elles sont de l'ordre de quelques
nanomètres. Il est cependant assez simple de coupler le
procédé PIII avec un procédé de dépôt
(de matériaux) classique.
cependant,
- Lors de l'implantation, aucune séparation de masse ne
peut être effectuée; tous les ions positifs présents dans
le plasma sont implantés. Il est néanmoins nécessaire que
ces ions possèdent une énergie suffisante.
- En théorie, plus les impulsions sont importantes
(très haute tension négatives), meilleure sera l'implantation; en
réalité, les tensions de travail sont limitées et il est
ainsi très difficile
d'implanter certains ions. Les tensions limites sont voisines
de 100 kV. En effet pour ces tensions élevées, le matériel
serait trop coûteux.
Comme nous venons de le voir, l'implantation ionique par
immersion plasma est une technique de traitement de surface des
matériaux, qui permet de modifier les propriétés
mécaniques d'une surface sans altérer le contenu du
matériau. Cette technique peut être utilisée dans des
domaines variés de l'industrie et tend à remplacer la
méthode conventionnelle (par faisceau d'ions) qui présentent des
limitations telles que la directivité du faisceau (impossibilité
d'implanter des formes tridimensionnelles), faible vitesse d'implantation,
coût d'investissement élevé. Le procédé PIII
peut être appliqué dans de nombreux domaines. Il fait l'objet de
nombreux travaux de recherche, qui portent notamment sur la
compréhension des interactions plasma-surface.
1.3 APPLICATIONS DE L'IMPLANTATION IONIQUE
L'implantation a d'abord été utilisée
dans la microélectronique pour le dopage des semi conducteurs. Par la
suite l'industrie mécanique a utilisé cette technique pour le
traitement des surfaces. On obtient des améliorations
intéressantes de la tenue à l'usure, à la fatigue,
à la corrosion et à l'oxydation; le champ des applications couvre
les outillages de mise en forme, les composants pour l'aéronautique, les
applications biomédicales (prothèses orthopédiques,
instruments chirurgicaux)...
Il est possible d'introduire des ions (12 à 18 pourcent
de Cr dans un acier ou Pd dans Ti) favorisant la formation d'un film passif
(film protecteur vis-à-vis de la corrosion), ou d'amorphiser les
surfaces et ainsi supprimer les joints de grains métalliques pour
éviter la corrosion des matériaux. Certains
éléments limitent l'oxydation à haute température,
par exemple les terres rares dans les aciers au chrome. De même
l'implantation d'Aluminium dans des alliages fer-chrome peut réduire le
taux d'oxydation de 10% à 1100°C.
Dans les céramiques qui sont des matériaux
particulièrement fragiles, la plupart des ruptures s'amorcent en
surface. Il est donc possible de les consolider (SiC, Si3N4, Al2O3,...) par
implantation d'ions métalliques (Cr, Ti, Zr, Fe...).
Au niveau des polymères, les modifications des
propriétés de surface sont la conséquence de celles
appliquées aux liaisons sous l'effet de l'énergie apportée
par les ions. On peut rompre les chaînes ou au contraire en créer
des nouvelles, provoquer des réticulations qui sont des
établissements de liaisons pontales entre les chaînes[4].
En microélectronique, l'implantation d'ions dans les
semi-conducteurs, sert surtout à modifier leurs propriétés
électriques. Concernant les dispositifs électroniques, deux
utilisations majeures ressortent : le dopage local (p ou n) du silicium et la
réalisation des substrats de silicium sur isolant (SOI).
L'activité électrique dans les circuits rapides à
très haut degré d'intégration, doit être
confinée à des couches extrêmement minces de
semi-conducteurs et les interférences électriques entre les
éléments du circuit adjacent doivent être
minimisées. L'une des façons d'y parvenir consiste à
créer des circuits dans un substrat de silicium sur isolant.
L'implantation d'oxygène dans un substrat de silicium permet de former
des couches isolantes d'oxyde enterré dans le silicium. On fabrique
ensuite les éléments du circuit dans le film superficiel,
électroniquement isolé. En revanche, dans les métaux, ce
sont les modifications mécaniques et chimiques de la couche
superficielle qui sont les plus intéressantes. En dehors des
applications à l'élaboration de couches superficielles
fonctionnelles à la surface des matériaux, une application
à l'implantation ionique est la coloration des métaux. Comme dans
ce procédé il est possible d'implanter n'importe quel
élément ionisé dans n'importe quel type de
matériau, il est ainsi possible d'obtenir plusieurs couleurs suivant le
type d'ion implanté.
Nous voyons que hormis le dopage des matériaux
semi-conducteurs, ces deux techniques s'élargissent à d'autres
domaines tels que le traitement de surfaces, la fabrication des couches minces
ou l'élaboration des structures SOI.
1.4 RECUIT POST-IMPLANTATION
Après l'implantation, les matériaux sont
généralement fortement dégradés : les
impuretés sont implantées sur des sites quelconques (elles ne
sont pas toutes en position substitutionnelle) et la plupart sont
électriquement inactives; rendant ainsi le matériau moins utile.
C'est pourquoi, Lors des applications en microélectronique, il est
souvent nécessaire de faire subir au matériau implanté un
traitement thermique particulier que l'on appelle recuit. Celui-ci a deux
rôles majeurs :
- Restaurer la structure cristalline du matériau, en
'guérissant' les défauts,
Activer les impuretés implantées.
Il faut noter qu'après recuit, la distribution des
impuretés dans le matériau est élargie. Si le
matériau est amorphe, les trajectoires des ions sont aléatoires
car aucune direction n'est alors privilégiée. Dès lors, on
assiste à la formation des bulles (cas oil l'ion implanté est un
gaz) ou des cavités (entités vides dues à l'implantation
d'ions métalliques) dans le matériau.
1.5 FORMATION DES NANO-CAVITES
1.5.1 Précurseurs
Lors de l'implantation ionique, une large zone amorphe est
créée, la densité du matériau dans la zone
endommagée diminue. Ainsi tous les paramètres d'implantation
(taille, densité, concentration d'ions, température) pris au
cours des phénomènes mèneront à une phase
d'implantation qui va générer des sites précurseurs des
cavités/bulles; ces sites sont des complexes lacunes-particules.
Du point de vue cavité, Romain DELAMARE[5] remarque que
le pic de distribution des lacunes créées se situe un peu avant
le pic de distribution des ions implantés. Ce qui lui permet de
séparer la zone complexe formée en trois. La première
zone, la plus proche de la surface, est principalement composée de
défauts lacunaires et de quelques atomes implantés. La seconde,
quant à elle, est une zone oil l'on trouve à la fois des lacunes
et des particules implantées. Enfin la dernière zone est
composée principalement de particules en position interstitielle et de
quelques lacunes. Les phénomènes de croissance des cavités
dans les matériaux semi-conducteurs ne sont pas encore bien
appréhender, ce ne sont que les paramètres (dose, énergie,
etc.) d'implantation qui sont pris en compte. Selon la dose d'implantation, il
y aura une phase de l'implantation qui va générer les sites
précurseurs des cavités. Ces sites sont des complexes
lacunes-particules.
Du point de vue des bulles[6], la nucléation se fait
par un mécanisme de mutation de piège (trap-mutation[7]).
Premièrement, c'est un atome qui va occuper un site vacant dans la
matrice, formant ainsi un complexe I-V. Ensuite d'autres atomes viendront
s'ajouter a ce complexe pour former un deuxième complexe ion-lacune
(I7-V) due à l'accumulation des atomes dans une seule lacune.
Dès lors que la pression dans ce complexe augmente, il peut avoir
éjection d'un atome de la matrice de son site cristallographique,
générant une lacune supplémentaire associée au
complexe I7+1 -- V2 ; l'atome déplacé se mettant alors en
position interstitielle : I7 -- V + I --* I7+1 -- V2 + i. La
formation de ces complexes lacunaires partiellement remplis d'ions nous donne
des précurseurs, qui vont donner naissance aux cavités/bulles
durant la phase de recuit post-implantation.
1.5.2 Création des nano-cavités
Le phénomène de création (ou
nucléation) des cavités reste compliqué à
décrire; seules des simulations [1] permettraient d'appréhender
ces mécanismes. Lors du recuit post-implantation, si la
température est suffisamment élevée, des complexes
(lacunes-particules ou ions-lacunes) créés par l'implantation,
lacunes et interstitiels en nombre égal, migrent et peuvent rencontrer
d'autres
complexes (précurseurs). Plusieurs cas sont possibles :
- Un interstitiel rencontre une lacune : la lacune et
l'interstitiel s'annihilent. Les lacunes tendent à créer des
cavités tandis que les interstitiels contribuent à leur
disparition.
- Un défaut ponctuel arrive sur un puits (surface, joint
de grains, dislocation ...) oil il s'élimine. - Des défauts du
même type peuvent se rassembler et former des petits amas.
Les amas formés par migration des complexes
lacunes-particules vont libérer les particules, qui iront occuper les
positions interstitielles dans le matériau; ainsi donc les amas seront
essentiellement constitués de lacunes pour donner naissance à une
cavité. Dans certaines conditions l'évolution de l'amas de
lacunes peut être totalement différente : l'amas grossit par
absorption de lacunes mais il conserve une forme sensiblement sphérique
ou polyédrique. On obtient une cavité, défaut stable dans
le matériau.
Pour les interstitiels la situation est plus simple, en effet
les amas d'interstitiels se transforment toujours en boucles de dislocations
(figure 1.6) qui peuvent croître en absorbant de nouveaux interstitiels.
Lorsqu'elles atteignent les limites du cristal, elles disparaissent en laissant
un plan d'atomes supplémentaires. Cependant, les complexes ions-lacunes
formeront à leur tour, des amas qui, pendant le recuit libéreront
du gaz en donnant naissance aux bulles.

FIGURE 1.6: boucle de dislocations formées dans le
matériau. [5]
D'après J. Grisolia[7], plusieurs types de cavités
sont observés après une implantation d'hydrogène, ou
d'hélium suivies d'un recuit. On observe:
- 1. Les platelets ou cavités plates orientées
suivant les plans (100)
Ces défauts plans sont observés lors de bilans
thermiques faibles (en dessous de 400°C). Ces platelets apparaissent
parallèles à la surface de la plaquette semi-conductrice et sont
situés à l'intérieur de la zone perturbée. Ces
cavités sont des défauts bidimensionnels de forme circulaire et
d'épaisseur constante.
- 2. Les cavités plates (111)
Contrairement aux cavités (100), les cavités
(111) ne sont pas situées au niveau de la zone d'arrêt des ions,
mais plutôt en fin de zone perturbée. Ces défauts ont une
épaisseur comparable mais leur taille est toujours supérieure
à celle des cavités (100) ; ils sont également
bidimensionnels; sont observées pour des bilans thermiques allant
jusqu'à 500°C.
- 3. Les cavités cylindriques
Ce type de defauts apparaît pour des bilans thermiques
intermédiaires (500 à 700°C). Il apparaît sous une
forme cylindrique d'orientation quelconque dans la zone perturbée. Son
diamètre est compris entre 2 et 4 nm et sa longueur varie en fonction de
la nature du recuit. Ces défauts sont des cavités filiformes.

FIGURE 1.7: Image en haute résolution d'une
cavité sphérique.[5]
4. Les cavités sphériques
Ces cavités sont essentiellement observées
à haute température (à partir de 700°C). Il
apparaît sous la forme d'une sphère et se situe dans la zone
perturbée. Sa taille (environ 2,5 nm) évolue avec la nature du
recuit.
Elles se situent dans la zone d'implantation des atomes
d'hélium et forment une bande qui peut

FIGURE 1.8: Exemple de cavités facettées ou non
obtenues pour une implantation à 1,55 MeV de 5.1016
He/cm-2 et un recuit de 700°C pendant une heure. [5]
s'étendre jusqu'à 1 um de large. Certaines d'entre
elles se facettent au cours de leur évolution pour minimiser leur
énergie avec le réseau[5].
1.6 CONCLUSION DU CHAPITRE
L'implantation ionique consiste à doper un
matériau d'une part, à l'aide d'un faisceau de dopants
ionisés avec ses atomes constituants; d'autre part à l'aide
d'immersion plasma. Ces deux techniques d'implantation présentent des
avantages et des inconvénients, chacune, trouvant son application dans
des industries.
Cependant, l'une des conséquences de l'implantation
ionique dans une matrice après recuit est la formation de
nano-cavités. Ces nano-cavités, importantes dans
l'élaboration des couches minces, permettra d'obtenir des structures SOI
par le procédé Smart Cut. Hormis ce procédé bien
connu, les nano-cavités peuvent servir à décontaminer, par
piégeage (ou gettering), les couches minces des impuretés
métalliques créées par implantation ionique avant recuit.
Cette pollution pouvant devenir un frein à l'élaboration des
nanostructures pour les cellules solaires.
CHAPITRE DEUX
APPLICATIONS POTENTIELLES DES
NANO-CAVITES
Le coût élevé de production des cellules
solaires est dû au coût des plaquettes de silicium massif, c'est
à dire le prix de la matière première, de la mise en forme
des lingots et de la découpe des lingots. Il est donc clair que la
réduction du coût du module (élement constitutif d'une
plaque solaire) passe par la réduction du coût de
l'élaboration du substrat. La méthode la plus accessible pour les
industriels est la réduction de l'épaisseur des plaques de
silicium c.-à-d. en films minces. La réduction de
l'épaisseur des plaquettes est aujourd'hui un point clé du
développement des cellules solaires photovoltaïques en silicium.
Actuellement les substrats de type silicium sur isolant (SOI)
présentent un très grand intérêt pour des
applications microélectroniques dans le domaine de la basse
consommation. Il existe plusieurs procédés d'obtention de
substrats SOI. Les plus utilisés aujourd'hui sont le
procédé SIMOX (de l'expression anglo-saxonne Separation by
Implantation of Oxygène, consiste à implanter de l'oxygène
dans un substrat de silicium à haute dose (1018
O+/cm2) afin de former une couche d'oxyde enterrée), le
procédé BESOI ((Bond and Etch-back SOI) qui est basée sur
le collage direct de deux plaquettes de silicium) et les procédés
basés sur le collage par adhésion moléculaire et
implantation ionique (SMART CUT). Pour obtenir des couches minces de silicium
sur de la silice, ces procédés, utilisant le collage par
adhésion moléculaire, sont combinés à des
procédés d'amincissement où le clivage d'un substrat est
obtenu par coalescence, provoqué par un traitement thermique, de
nano-cavités générées par implantation ionique.
Dans ce chapitre, nous nous intéresserons au
procédé Smart Cut et la méthode de purification des
couches minces.

2.1 PROCEDE SMART CUT
Les structures SOI sont constituées d'une fine couche
de semi-conducteur (parfois le silicium) sur une couche isolante (souvent de
l'oxyde de silicium) permettant la fabrication de circuits
intégrés très efficaces et très rapides. En effet,
il n'existe donc pas de contact entre la couche du semi-conducteur et son
substrat, qui a pour avantage de réduire les effets capacitifs parasites
ainsi que les fuites dues au substrat et d'augmenter le gain en courant
(consommation élevée de courant) [3]. L'un des principaux
domaines d'application de cette technologie est le marché des
systèmes portables d'où l'intérêt
général qui lui est accordé.
Nous vous présenterons donc ici cette technique (le
procédé smart cut) de production de ces structures très
utilisées dans l'industrie.
Smart Cut (Super Material Abrasive Resistant Tools) est un
procédé technologique permettant le transfert de films minces de
matériaux cristallins sur des substrats. Cette technique est une
combinaison de l'implantation d'hydrogène suivie du collage par
l'adhérence moléculaire direct. Dans ce procédé, la
fabrication d'une couche mince de matériau semi-conducteur comprend
l'exposition d'une plaquette de matériau semi-conducteur,
- à une étape de bombardement d'une face du
substrat avec des ions, afin d'implanter ces ions en dose suffisante pour
créer une couche de nano-cavités (couche H),
- à une étape de mise en contact intime de cette
face du substrat réalisée par liaisons hydrophiles entre les deux
plaquettes, et
- à une étape de traitement thermique pour
générer un clivage du substrat au niveau de la couche de
nano-cavités.
Dans ce procédé, la zone où s'effectue
l'implantation est perturbée, ce qui conditionne
l'homogénéité du film mince et sa rugosité au
niveau des surfaces situées de part et d'autre de la surface de clivage.
Il est donc ensuite nécessaire de réaliser des traitements
thermiques pour éliminer les défauts, les rugosités, etc.
Puis un polissage est nécessaire. Le reste de la plaquette donneuse est
intact et peut être recyclé pour former une autre plaquette
support, ce qui diminue le coût matériel.
Comme toute technologie, celle-ci présente des
avantages : on a la possibilité de choisir l'épaisseur de la
couche tout en modifiant juste l'énergie d'implantation ionique, ce qui
nous donne une couche uniforme avec très peu de défauts, et le
recyclage de plaque permet une production à faible coût.
Cependant, la structure atomique du matériau est modifiée,
réduisant ainsi la résistance à la brisure du
matériau; aussi, les propriétés physico-chimiques sont
modifiées entrainant une destruction de la structure cristalline.


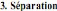
FIGURE 2.1: Etapes du procédé Smart Cut.
Nous pouvons donc conclure cette partie en disant que
Smart-Cut est une technologie de production avancée des systèmes
SOI. Cela requiert tout le nécessaire pour l'élaboration et la
fabrication des plaquettes SOI, qui améliore les performances des
circuits intégrés. Comme mentionné plus haut, cette
technologie s'applique également à d'autres semi-conducteurs
(SiC, GaAs, InP,). En utilisant une couche mince plutôt que le
matériau massif (qui est très coûteux), cela permettrait de
réduire les coûts de fabrication car les couches minces ainsi
créées sont autosupportées et peuvent être
transférées par la suite sur des substrats compatibles de
très faible coût (verres, céramiques, ).
Dans l'industrie du semi-conducteur, la contamination du
silicium par des impuretés métalliques, notamment lors de
traitements thermiques à haute température, entraîne une
dégradation des caractéristiques électriques (pour les
cellules solaires) ainsi que des problèmes de fiabilité.
Jusqu'à présent, l'étape de piégeage était
remplie par une étape de diffusion de phosphore après un
dépôt de POCl3. Cependant cette technique n'est pas toujours
suffisante ou même possible sur certains types de composants. Une
alternative prometteuse est le piégeage par implantation ionique.
L'évolution des défauts créés par implantation
ionique, ainsi que la cinétique de piégeage d'une impureté
métallique, seront mis en évidence dans cette partie.
2.2 GETTERING (PIEGEAGE D'IMPURETES)
Le terme anglais gettering qui signifie piégeage est un
procédé par lequel des impuretés indésirables sont
retirées dans un endroit alternatif (le piège) du matériau
oil ils préfèrent résider (leur énergie est
faible).
Dans le but de faire des économies, au lieu d'utiliser
le silicium pur qui coûte cher, on utilise le silicium massif renfermant
trop d'impuretés. Les couches minces destinées à
l'énergie solaire sont généralement celles qui
présentent le plus de contamination métalliques. Et les moyens
pour leur décontamination font l'objet de différentes
études. Le gettering par les nano-cavités induites par
implantation d'ions est l'une des pistes les plus prometteuses.
Les impuretés introduites dans les composants pendant
leur fabrication modifient les caractéristiques de ceux-ci. Il est donc
impératif de contrôler la concentration de ces impuretés,
d'autant plus que la miniaturisation des composants les rend de plus en plus
sensibles à celles-ci. La plupart de ces impuretés sont en fait
des impuretés métalliques dues aux différents
procédés de fabrication des composants. Les nano cavités
formées par implantation d'ions (H ou He) sont des puits efficaces pour
les impuretés métalliques dans les matériaux (Si).
Comparé au piégeage traditionnel à l'équilibre
thermodynamique qu'est le dopage (diffusion de phosphore après un
dépôt de POCl3), l'implantation ionique présente de
nombreux avantages, (i) les puits créés par implantation peuvent
se situer très près de la zone active. La figure 2.2
schématise ce phénomène de façon succinte.
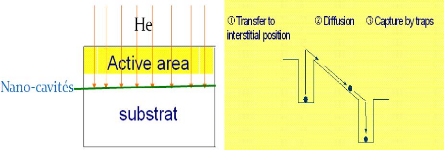
FIGURE 2.2: Processus de piégeage (gettering).
Aussi, le piégeage des impuretés
métalliques par des nano-cavités est une voie prometteuse
pour
obtenir des échantillons de silicium de haute pureté. La
formation-croissance dans un
matériau, de couches de nano-cavités à
des profondeurs déterminées (notamment près des surfaces
libres) par implantation d'ions, suivi de recuit met en jeu des interactions
complexes entre ces ions et les amas de lacunes[9].
Une des méthodes les plus utilisée est une
méthode de piégeage par la face arrière, qui implique de
forts bilans thermiques donc de forts coûts. Une des alternatives
à cette méthode est l'utilisation des nano cavités
induites par implantation d'hélium pour piéger les
impuretés en dehors des zones actives des composants. Il s'agit du
gettering de proximité. Par des techniques de piégeage, nous
verrons comment les nano-cavités induites permettent de purifier
à faible coût certains semi-conducteurs (silicium) et par
conséquence de réduire le coût des composants.
2.2.1 Les différentes méthodes de
piégeage
Suivant la nature des sites pièges, ces méthodes
sont séparées en deux catégories distinctes, à
savoir : le gettering interne, celle qui utilise comme sites pièges des
défauts déjà présents dans le silicium et le
gettering externe, celle oil l'on crée les défauts qui vont
servir de pièges.
Le gettering interne
Ce terme désigne une méthode qui utilise la
précipitation de l'oxygène, présent dans les substrats,
comme site piège. En effet, dans ce substrat, on trouve une grande
concentration de précipités d'oxygène. Cette
précipitation de l'oxygène crée dans les substrats des
faisceaux qui se développent sans interruption, présentent des
défauts. Par la suite, ces défauts atteignent des zones actives,
formant au passage des nano-cavités qui serviront de pièges aux
impuretés. Une description de cette méthode consiste en une
succession de recuits permettant de créer des nano-cavités/bulles
ou précipités qui diffuseront vers la surface pour y former des
sites pièges; en effet, lors de la croissance des
précipités d'oxygène, des auto-interstitiels vont
être émis. Et ce sont ces auto-interstitiels qui vont favoriser la
précipitation des impuretés afin qu'elles soient
piégées. Enfin, les impuretés piégées
restent présentes dans le matériau et peuvent donc se
libérer au cours de recuits ultérieurs.
Le gros avantage de cette méthode est qu'elle est
facile à mettre en oeuvre sur une chaîne de production et les
pièges internes sont plus près des zones actives que sur la face
arrière. Par contre, l'homogénéité des
caractéristiques des composants est mauvaise (ceci vient du fait que
l'on ne peut pas contrôler la distribution et la taille des
précipités d'oxygène). Cette méthode n'est efficace
qu'avec des impuretés en grande concentration et qui précipitent
facilement.
Le gettering externe
Il existe deux façons de réaliser du gettering
externe : on introduit les sites pièges, soit par la face
arrière, soit par la face avant.
Si on introduit les défauts par la face arrière,
alors il suffit de faire diffuser l'impureté et de la faire
précipiter dans la zone de nano-cavités. L'avantage de cette
méthode est qu'elle est facile à mettre en uvre et que l'on peut
éliminer la zone de piège. Par contre elle nécessite des
bilans thermiques importants et elle ne piège pas les impuretés
dont la concentration est inférieure à leur solubilité
limite.
Lorsque l'on introduit des défauts par la face avant,
c'est à dire que des nano-cavités (sites de piégeage) se
créent près des zones actives par implantation ionique, on parle
alors de gettering de proximité comme mentionné plus haut.
Faire donc croître des nano-cavités dans des
matériaux permettra la réalisation de ces pièges. Mais ces
nano-cavités nécessitent de fortes doses d'implantation et cela
crée des défauts qui risquent de perturber les zones actives. A
cela donc, l'immersion plasma (d'hydrogène) est un atout, les
interactions plasma-surface créent des zones actives non
perturbées par les défauts car cette méthode ne
présente pas de problème à caractère directionnel.
De plus la présence d'hydrogène favorise le transfert entre les
nano cavités.
2.3 CONCLUSION DU CHAPITRE
Nous avons vu qu'après des implantations ioniques, des
nano-cavités/bulles sont formées pendant le recuit, dans les
semi-conducteurs. Dans ce chapitre, nous voyons leurs applications qui sont de
plus en plus utilisées : d'une part la fabrication de structures SOI par
l'intermédiaire du procédé Smart Cut dans le cas des
implantations d'hydrogène oil les cavités induites après
recuit permettent l'élimination des micros défauts et
l'hydrogène à la surface pour obtenir une nouvelle couche pure,
mince et à faible coût; aussi des dérivées de ce
procédé, ont permis la mise sur pieds des structures ULSI
(composants d'ultra haute intégration : des milliers de transistors dans
une seule puce électronique) et des matériaux à faible
constante diélectrique dit "`low-k materials'". D'autre part, le
piégeage des impuretés métalliques (gettering) par
implantations d'ions oil les nano-cavités/bulles induites servent de
pièges aux impuretés métalliques (purification). Lors de
ce procédé de fabrication et méthode
de purification, nous avons vu l'importance des
nano-cavités, qui nécessitent évidemment une croissance
pendant le recuit post-implantation (croissance thermique). L'étude de
cette croissance thermique nous permettra de mieux comprendre leur impact
technologique dans les semi-conducteurs.
CHApiTRE TRois
CROISSANCE DES
NANO-CAVITES/BULLES
La terminologie généralement utilisée dans
la littérature désigne les bulles comme des entités
remplies de gaz tandis que les nano-cavités sont supposées
vides
3.1 CROISSANCE THERMIQUE DES NANO-CAVITES
Après implantation ionique, les
nano-cavités/bulles formées croissent au cours du traitement
thermique (figure 3.1). Pour décrire cette croissance, deux
mécanismes ont été proposés dans la
littérature. Ils peuvent s'appliquer soit aux nano-cavités, soit
aux bulles. Il s'agit des mécanismes d'Oswald Ripening (OR) et de
Migration Coalescence (MC).

FIGURE 3.1: Croissance thermique de nano-cavités, cas
d'implantation de l'As [E. Ntsoenzok].
3.1.1 La Migration Coalescence
Le mécanisme de migration coalescence (MC) suppose que
les nano-cavités/bulles migrent et fusionnent lorsqu'elles se
rencontrent (figure 3.2); c'est un mécanisme de collision
considérant le mouvement des nano-cavités/bulles elles
mêmes. Leurs mouvements sont attribués
au transfert de lacunes dans les nano-cavités.
Le coefficient de diffusion Dc d'une cavité/bulle
dépend à la fois de son rayon (r) et de la pression interne de
l'ion implanté (p). Il prend en compte les mécanismes de
diffusion de la surface et du volume de la bulle/cavité, ainsi que le
transport de l'ion implanté en phase gazeuse. Le coefficient de
diffusion Dc (r, p) étant inversement proportionnel au rayon,
les petites nano-cavités/bulles diffusent plus vite vers les autres
nano-cavités/bulles pour coalescer. Elles ont donc tendance à
disparaitre les premières. D'après ce mécanisme, la
croissance des nano-cavités/bulles s'arrête lorsque leur longueur
de diffusion est supérieure à la distance qui les
sépare.
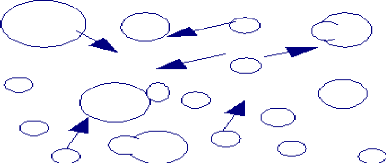
FIGURE 3.2: Processus de migration coalescence.
Ce mécanisme a été modélisé
par J. H. Evans [1] dans le cas d'une étude des mécanismes de
croissance des bulles d'hélium implantées dans le silicium. C'est
un modèle simple dont l'étude révèle des richesses
insoupçonnées. Dans ce modèle, l'équation de base
gouvernant la vitesse de fusion ou de coalescence des
nano-cavités/bulles (ayant un rayon r et une concentration
Cv) migrant aléatoirement a été décrite
et simplifiée pour l'application présente. Elle est de la forme
:
dCv
dt
= 16ðDcrC2 (3.1)
v
De cette équation (voir annexe), il a été
établi une relation entre le rayon des nano-cavités et le temps
de recuit :
~4/3
12S ~4ð
r2 -- r2 o = D5t (3.2)
ð 3
On s'aperçoit qu'effectivement, dans la croissance des
nano-cavités/bulles par la MC, le rayon moyen en fonction du temps de
recuit (t) suit une loi comportementale en /t donnée par
l'équation :
r2--r2 o =Kt (3.3)
Où Dc : coefficient de diffusion d'une
cavité, r : rayon moyen des cavités, S : surface de la
cavité, r0 : rayon moyen initial des cavités, D5 :
coefficient de diffusion surfacique et K une constante.
3.1.2 L'Oswald Ripening (Maturation d'Oswald)
Ce processus spontané se produit parce que de grandes
particules sont énergétiquement favorisées aux
dépens de petites particules et les petites particules
cinétiquement favorisées aux dépens des grandes. Ceci
s'explique par le rapport volume/surface (que nous noterons Ù S ); les
petites particules ont un Ù S élevé et sont par
conséquent plus facile à produire, contrairement aux grandes
particules qui avec leur Ù S petit, représente un état de
faible énergie (état obtenu en abaissant la température
lors du recuit thermique). De ce fait, les petites particules atteindront un
état de faible énergie si elles sont transformées en
grandes particules; c'est le phénomène de maturation
d'Ostwald.

FIGURE 3.3: Processus d'oswald ripening
Il décrit aussi l'évolution temporelle d'une
structure inhomogène basée sur le fait que les concentrations de
l'atome implanté et de lacunes à la périphérie des
nano-cavités/bulles
sont inversement proportionnelles à leur rayon. Un
gradient de concentration se créé entre les
nano-cavités/bulles de différentes tailles; ce qui conduit la
diffusion de lacunes et d'atomes implantés d'une cavité/bulle
à une autre (figure3.3) à travers la matrice et monopolise la
croissance ou le rétrécissement jusqu'à ce que la taille
des nano-cavités/bulles s'homogénéise ou que les distances
entre les nano-cavités/bulles deviennent trop importantes.
Dans l'approche LSW 1 , le rayon moyen d'une
cavité/bulle suit une loi comportementale en fonction du temps qui
obéît à l'équation :
(4 )
r3 - r3 o = aDct (3.4)
9
Où ro est le rayon moyen initial et a est
proportionnel à l'énergie spécifique d'interface.
En effet, il n'existe pas de difficulté dans
l'application de la maturation d'Oswald (OR) à une population de
nano-cavités/bulles. L'équation maîtresse décrivant
ce mécanisme a été établie par Greenwood et al.[1]
dans une étude approfondie de la croissance des bulles dans les
métaux. Ils trouvèrent à cet effet que le taux de
variation du rayon pouvait s'exprimer comme suit :
dr
dt
(1 ) (2ãI )
= - DcCeq
v exp (3.5)
r rkT
Où Ceq
v : concentration à l'équilibre d'une lacune,
ã : l'énergie surfacique, I : volume de la cavité, k :
constante de boltzman, T : température de recuit.
Sous de bonnes conditions donc, l'OR se produira à
travers la dépendance en 1 r de l'équation, qui doit mener
à la croissance de grosses nano-cavités/bulles aux dépends
des plus petites; le terme en exponentiel dans l'expression du rayon deviendra
donc plus dominant et accélérera rapidement le processus de
rétrécissement. En se rétrécissant, les lacunes de
certaines nano-cavités/bulles seront redistribuées à
d'autres et à la fin on aura un nombre réduit de
nano-cavités/bulles ayant de très grands rayons. Nous pouvons
observer ce phénomène sur la figure 3.4 [8] sur laquelle nous
voyons le nombre de nano-cavités diminuer avec l'évolution
temporelle (pendant le recuit).
Ce mécanisme, du fait de la prise en compte de certains
facteurs, peut très bien limiter la croissance. Par exemple J. Evans a
prédit que l'effet de perte de lacunes à la surface pouvait
limiter la croissance des bulles. C'est pour de telles raisons que certains
chercheurs ont réalisé une étude comparative des deux
mécanismes.
1. La théorie Lifshitz-Slysosov-Wagner
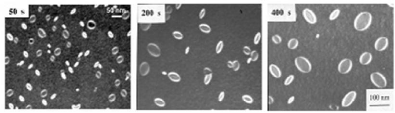
FIGURE 3.4: Croissance de nano-cavités suivant le
mécanisme d'Oswald ripening
3.1.3 Comparaison des deux mécanismes de
croissance
A partir des lois de croissance des rayons des bulles en
fonction des temps de recuit, Schroeder et al [11] ont montré que les
mécanismes de croissance par migration coalescence et par Oswald
Ripening présentent des invariants qui permettent de les
différencier. Ils ont spécialement utilisé les
dérivées logarithmiques d ln r
d ln t pour la comparaison avec des modèles de
croissance parce que celles-ci sont indépendantes de la valeur absolue
des diverses propriétés du matériau, qui ne sont
précisément pas connues.
Cependant, il peut être très difficile ou
impossible d'identifier le mécanisme de croissance opérant car
les résultats expérimentaux sont parfois différents des
théories prédites.
Pour clarifier ce problème et avoir une meilleure
compréhension de la question : quel mécanisme gouverne la
croissance et dans quelles conditions? Des auteurs ont essayé des
approches différentes en choisissant les paramètres
expérimentaux de façon à tester les invariances
spécifiques de MC et OR.
Dans le cas de la migration coalescence, pour une
température de recuit donnée, le rayon moyen des
nano-cavités ne change pas si le produit de la concentration
d'hélium implanté CHe par le temps de recuit ta reste
constant. Par contre dans le cas de l'Oswald Ripening, pour un temps de recuit
donné, le rayon moyen des nano-cavités ne dépend pas de la
concentration d'hélium implanté CHe, tandis que le
mécanisme de migration coalescence conduit à une augmentation du
rayon avec CHe.
Dans les métaux, les études faites sur la
croissance thermique des nano-cavités d'hélium ont montré
que les deux mécanismes de croissance (OR et MC) peuvent coexister[3,
13]. Les conditions de traitement des échantillons et le profil de la
couche de nano-cavités (densité, rayon des
nano-cavités,..) ainsi que la profondeur d'implantation sont des
paramètres qu'il faut considérer pour pouvoir déterminer
par quel mécanisme la croissance s'opère.

FIGURE 3.5: Représentation des invariances du rayon moyen
des nano-cavités/bulles en fonction de la concentration d'hélium
pour les différents mécanismes de croissance, MC et OR
3.2 INTERET DE L'ETUDE DES NANO-CAVITES/BULLES
Les implantations d'hydrogène et d'hélium
à hautes doses sont connues pour former des nano-cavités dans les
semi-conducteurs. Ces nano-cavités/bulles ont des applications qui sont
de plus en plus utilisées :
Dans les réacteurs nucléaires [6], les
métaux utilisés comme armatures sont soumis à de fortes
irradiations par des neutrons (14 MeV pour les réactions de fusion
Deutérium-Tritium). Ces irradiations peuvent produire des atomes
d'hélium par des réactions de transmutation et conduire ainsi
à la formation de bulles d'hélium dans le métal. Ces
bulles peuvent conduire à une dégradation des
propriétés du métal et poser de véritables
problèmes de sécurité ainsi que des problèmes
économiques pour les réacteurs nucléaires. C'est pour
éviter au maximum ces effets néfastes que l'étude des
bulles dans les métaux est un sujet de recherche largement
répandu.
Dans le silicium, les nano-cavités induites ont des
applications telles que : la fabrication de structures SOI (Silicon On
Insulator) par l'intermédiaire du procédé Smart-Cut dans
le cas des implantations d'hydrogène; le piégeage des
impuretés métalliques (gettering) pour les implantations
d'hélium.
Il est à noter que c'est pendant les recuits
post-implantations que la croissance proprement
dite des nano-cavités/bulles va intervenir.
3.3 SIMULATIONS NUMERIQUES
Pour ce mémoire de D.E.A, nous avons choisi de simuler
la croissance des nano-cavités/bulles au cours du recuit
post-implantation. Nous avons employé des méthodes empiriques
afin de décrire l'évolution de la taille des
nano-cavités/bulles au cours du temps et en fonction de la
température, en considérant le pénomène OR comme
dominant la croissance des nanocavités/bulles dans un matériau
lors du recuit.
3.3.1 Modèle de croissance par Oswald Ripening
On considère une distribution des rayons de N
nano-cavités qui seront programmées pour passer par les cycles
successifs de retrécissement-croissance afin de simuler le processus OR.
La distribution initiale est gaussienne. La variation /ri du rayon ri (1 i N)
de la cavité i pendant l'intervalle de temps /t est donnée par
l'équation :
( 1 ) ( 2ãÙ )
/ri = -/t DcCeq
v exp (3.6)
ri rikT
Ce qui correspond à un rétrécissement, donc
à une libération de lacunes, dont le nombre /N est donné
par l'expression :
i /Ù)
/N = > (/ri4ðr2 (3.7)
Lors du retrécissement, certaines nano-cavités
retrécissent plus vite que d'autres. Alors, pour éviter que le
système de nano-cavités ne rétrécisse rapidement
(ce qui pourrait conduire à une disparition de toutes les
nano-cavités), une condition dite de 'tronquage' a été
mise au point. Elle stipule que si une cavité a un rayon
inférieur au rayon seuil (que l'on fixera), elle est totalement
enlevée et ses lacunes distribuées aux autres
nano-cavités(la distribution n'est pas uniforme, les plus grandes
cavités recevront plus que les petites).
Dans la procédure de croissance, les lacunes
libérées et distribuées parmi les nano-cavités
restantes mèneront à une augmentation du rayon dont l'expression
est donnée par:
( > ) /N (Ù/4ðr2 )
dri = ri/ r (3.8)
i
Un problème pratique dans le programme concernera le
nombre de nano-cavités initial puis-
qu'il faut un nombre de nano-cavités de l'ordre de
5.106 dans un volume de 1,43055667.10_31 m3 pour
refléter la réalité physique, c'est-à-dire pour
finir avec un nombre de 200 nano-cavités. Avec un volume de
cavité constant, ce problème sera allégé en
présentant une procédure d'itération flexible dans
laquelle, après que le nombre initial de nano-cavités ait
diminué par un facteur de deux, un nouvel ensemble de
nano-cavités est généré. Cependant, rien ne serait
gagné si l'ensemble généré avait des
paramètres identiques aux nano-cavités de départ; donc les
nano-cavités re-générées ont été
données avec des rayons légèrement différents
(#177; 0,1%) des nano-cavités de départ, reflétant les
variations statistiques prévues des recuits réels. La
différence a été maintenue petite pour empêcher
l'élargissement significatif de la distribution des rayons. Cette
procédure d'itération du cycle de retour au nouveau nombre
original de rayons pourrait être répétée autant de
fois que possible.
Par la suite un nombre initial de 500 rayons
différents, avec une distribution gaussienne des rayons (r = 0,6 #177;
0,1 nm), sera employé, oil 0,1 est la valeur de sigma
représentant la diffusion du rayon. Clairement la clef à tout
mécanisme de simulation pratique est d'avoir accès aux bons
paramètres. Dans le cas du silicium, il existe un accord étroit
dans la littérature sur une expression pour Ceq
v , dont la valeur est centrale pour n'importe quelle
prévision du mécanisme OR. Bracht et al. [1] ont
dérivé pour le silicium la relation (en cm/s2) :
DcCeq
v = O, 92 exp (-4, 14eV/kT) (3.9)
précisant qu'elle ne dévie pas beaucoup du
résultat ancien de Tan et Gösele [1] qui ont obtenu :
DcCeq
v = O,6exp(-4,03eV/kT) (3.10)
Pour ce travail, on utilisera la relation (3.10). Un
paramètre moins important, mais pouvant avoir une influence sur les
résultats est celui de l'énergie surfacique (ã). Une
valeur de 1,295 J/m2 a été employée, comme
suggéré par J. H. Evans. De ce modèle, nous avons pu
élaborer un algorithme qui suivra les différentes étapes
suivantes :
1. Donner la durée du recuit t, le pas
d'incrémentation du temps /t et le nombre de cycles nécessaires
t Ät,
2. Considérer une distribution de différents
rayons de 500 nano-cavités obéissant à la loi
gaussienne,
3. Calculer le rétrécissement /ri des rayons
à partir de l'équation (3.6),
4. Calculer le nombre total /N de lacunes libérées
à partir de l'équation (3.7),
5. En déduire les nouveaux rayons après
rétrécissement ri = ri + Äri,
6. Tronquer les nano-cavités dont le rayon est
inférieur à un rayon seuil fixé et en déduire le
nombre de nano-cavités restantes,
7. Ajouter à ÄN, les lacunes issues des
cavités tronquées,
8. Calculer l'augmentation dri des rayons des
nano-cavités restantes par application de la relation (3.8),
9. Calculer les nouveaux rayons des nano-cavités
restantes ri = ri + dri,
10. A partir de la nouvelle distribution obtenue en 9
répéter les étapes 3 à 9 jusqu'à ce que le
nombre de cycles requis soit atteint.
3.3.2 Modèle de croissance par Migration
Coalescence
Le processus MC est une succession de deux
phénomènes : une migration des cavités et ensuite leur
coalescence (fusion) après un choc. Dans ce modèle qui reproduit
relativement bien les aspects les plus significatifs de ce processus, la
migration permet à différentes nanocavités de se
déplacer aléatoirement selon la cinétique de diffusion en
surface, en utilisant la relation de diffusion de nano-cavités dont le
coefficient est donné par la relation :
Ds = 130 exp(-2,45eV/kT) (3.11)
Quant à la coalescence qui est l'union entre deux ou
plusieurs nano-cavités pour en former une plus grosse, elle est
décrite comme suit : deux nano-cavités s'approchent de plus en
plus près, par migration bien sûr, jusqu'à une distance
ä, oil le lien entre les surfaces en contact se brise et la coalescence se
produit. Sur la figure 3.6 on schématise le phénomène de
coalescence entre deux particules.
De ces deux phénomènes, la coalescence est la
plus importante, plusieurs facteurs l'influencent à savoir : la
dimension d'une nano-cavité, la force d'impact, le champ
électrostatique, la vitesse de migration, etc. Si les
nano-cavités se déplacent rapidement (c.-à-d. pour des
températures de recuit élevées qui augmente l'agitation
thermique) le choc entre deux nano-cavités peut être fort et elles
pourront rebondir sans qu'il y ait coalescence. Il est donc évident que
la mise au point d'un modèle pour tenir compte de la coalescence
nécessitera un effort de simplification important.

FIGURE 3.6: Schéma représentatif du
phénomène de coalescence entre deux nano-cavités
La coalescence influence de façon significative la
croissance des nano-cavités. En effet en augmentant leur
diamètre, la coalescence affecte le volume du matériau et par le
fait même, ses propriétés structurales. Toutefois, le
phénomène est très complexe et dépend de nombreux
paramètres externes. Par conséquent, la modélisation de la
MC est un problème ouvert.
Un problème avec la modélisation des
événements de coalescence est que le processus mène
à une réduction du nombre de cavités et donc des calculs
statistiques. Dans la simulation de la maturation d'Ostwald des
nano-cavités dans le silicium[1], un problème analogue a
été traité en employant une procédure de clonage.
Dans le cas actuel, après que le nombre de nano-cavités ait
été réduit par un facteur de 4, le bloc sera cloné
et utilisé pour créer une surface irradiée de facteur
quatre fois plus grand, de ce fait retournant au nombre initial de
nano-cavités dans le système. Cette procédure
d'itération pourrait être répétée autant de
fois que possible.
De ce modèle, nous avons pu élaborer un algorithme
qui suivra les différentes étapes suivantes :
1. Donner la durée du recuit, la durée d'un cycle
et le nombre de cycles nécessaire,
2. Créer une liste qui contiendra les différents
rayons et les positions des nano-cavités,
3. Considérer une distribution de rayons
différents de 500 nano-cavités suivant la loi gaussienne bien
définie dans une cellule carrée de côté L,
4. Calculer les positions (x et y) des nano-cavités,
5. Pour une cavité donnée, tester le
critère de coalescence avec toutes les autres nanocavités,
6. En déduire le nombre de nano-cavités
restantes,
7. Calculer les nouveaux rayons des nano-cavités
restantes,
8. A partir de la nouvelle distribution obtenue
répéter les étapes 5 à 7 jusqu'à ce que le
nombre de cycles requis soit atteint.
3.3.3 Résultats de simulations et Discussions
Pour cette section, nous nous sommes uniquement attardés
sur le mécanisme par Oswald Ripening.
Résultats de simulation OR
Nous avons d'abord réalisé des tests sur les
différents paramètres de simulation à savoir : dt (pas
d'incrémentation du temps), l'expression de
DcCeq
v , le critère de tronquage des cavités, le
temps de recuit et vérifié l'équation aux dimensions des
différentes formules utilisées dans le programme. Au cours de ces
tests, nous avons pu observer des résultats traduisant le
phénomène de croissance (selon l'allure) étudié
pour un dt = 0.0001 s, un temps de recuit t = 1800 s et un critère
(tronquer toutes les cavités dont le rayon est inférieur à
1/3 du rayon moyen initial).
Concernant les tests sur le pas d'incrémentation du
temps, c'est un paramètre très important qui est pris tel que
toute cavité de rayon = 1/3 du rayon moyen initial est réduite et
ses lacunes distribuées aux cavités restantes. Nous avons pu
obtenir des résultats satisfaisants autour de deux valeurs (figure
3.7).
L'influence du nombre de cavités choisit a fait l'objet de
plusieurs tests afin de choisir celui pouvant refléter la
réalité physique (voir figure 3.8).
Les recuits ont été exécutés pour
un temps de 1800 s sur la gamme de température ambiante (700 - 1200
°C) pour obtenir la variation du diamètre moyen en fonction de la
température. Les résultats sont présentés sur la
figure 3.9 ainsi que trois ensembles de résultats de la
littérature (dont deux expérimentaux et une simulation) pour
lesquels l'effet de la température a été examiné[1]
pour des temps de recuit de 1800 ou 3600 s.
Il ressort qu'avec les paramètres utilisés, les
prévisions du mécanisme OR sont bien en-dessous des
résultats expérimentaux, pour les températures au
delà de 800°C. Vers 1000°C la nature du
phénomène est pertinente. De 700°C à 900°C, il
n'y a pratiquement aucun grossissement avec seulement une augmentation
marginale en diamètre moyen de

FIGURE 3.7: (a))Résultats des simulations de OR pour un
recuit de 1800 s en fonction de la température pour dt = 0,0001s;
(b))Résultats des simulations de OR pour un recuit de 1800 s en fonction
de la température pour dt = 0,001s.
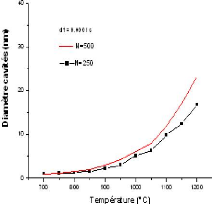
FIGURE 3.8: Influence du nombre de particules
0,999 à 1,946 nm. Au cas oil l'expression de
DcCeq
v serait remise en cause, l'ajustement au résultat
expérimental correspondant à un diamètre moyen de 8,5 nm
à 1800 s et à 700°C [1], necessiterait que la valeur de
DcCeq
v soit augmentée par un facteur de 106.
Un contrôle important du programme de simulation
était d'examiner si les résultats
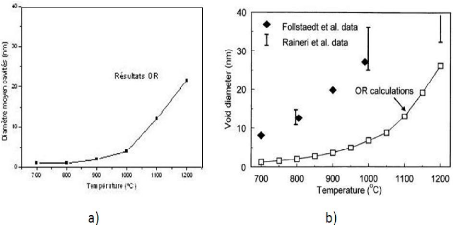
FIGURE 3.9: (a))Simulations de OR pour un recuit de 1800 s en
fonction de la température pour 500 nano-cavités;
(b))Résultats des simulations de OR par J. H. Evans pour un recuit de
1800 s en fonction de la température et comparaison avec deux
résultats expérimentaux.
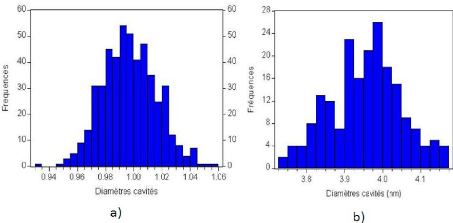
FIGURE 3.10: (a))Histogramme de la distribution initiale de
taille des nano-cavités/bulles pour un recuit à 1050°C;
(b))Histogramme de la distribution de taille des nano-cavités/bulles
pendant le recuit à 1050°C après 1800 s.
ont donné le caractère physique prévu par
le mécanisme OR. Les schémas a) et b) de la figures 3.10 sont des
histogrammes typiques de la distribution en taille des nano-cavités
calculée (avant et après recuit) oil cette
propriété est clairement vue. Les histogrammes n'étaient
pas toujours lisses.
De temps à autre des gaps sont apparus dans la
distribution établie. Après une croissance de nano-cavités
appréciable, la valeur du rayon moyen en fonction du temps obéit
à l'équation (3.4). Les résultats de recuit à 1100
et 1200°C sont représentés sur la figure 3.12. Pour des
températures basses, les résultats graphiques obtenus
étaient presque des droites.
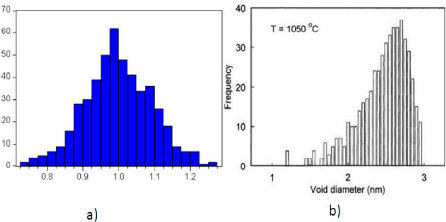
FIGURE 3.11: Histogramme de la distribution ((a) initiale; (b)
finale) de taille des nanocavités/bulles pendant un recuit à
1050°C par J. H. Evans.
Comme déjà indiqué, les résultats
présentés correspondent à un système fermé
oil le nombre de lacunes et le volume total des cavités demeurent
constants. Cependant, il est clair que dans le cas pratique, le
mécanisme OR doit donner la possibilité de perte de lacunes
à la surface et une variation du volume pendant le recuit. Une
perspective serait de prendre en compte cette perte sur la croissance par OR
des nano-nano-cavités/bulles.

FIGURE 3.12: (a)) : Graphe du rayon cubique en fonction du
temps pour calculs effectués à 1100°C et 1200°C; (b)) :
Graphe du rayon cubique en fonction du temps pour calculs effectués
à 1100°C et 1200°C par J. H. Evans.
CONCLUSION GENERALE
Le contrôle de la structuration des matériaux
à l'échelle nanométrique permet non seulement d'envisager
la réalisation de nombreuses applications nouvelles mais aussi de
pouvoir faire varier les propriétés de certains matériaux.
Une part importante des projets actuels concerne la production d'énergie
électrique : cellules solaires à couches minces ou à gel
de nanoparticules d'oxyde de titane, batteries à électrodes de
lithium, piles à hydrogène etc. Le secteur médical est
très impliqué, lui-aussi. Par exemple, des nanoparticules
encapsulées dans des petites billes creuses de polymères qui sont
injectées dans l'organisme, permettent d'améliorer certaines
techniques de scannage.
Le sujet traité ici, nous permet de comprendre et de
mieux contrôler le procédé de réalisation de ces
matériaux à l'échelle microscopique (couches minces), puis
la purification de ces couches au moyen du gettering qui est un
procédé ayant pour but d'optimiser le fonctionnement des
dispositifs à base semi-conducteurs, en débarrassant la zone
active des impuretés indésirables par des nano-cavités.
Ces impuretés sont alors regroupées dans une couche
enterrée endommagée et stable située sous une couche
supérieure d'excellente qualité cristalline. L'implantation
ionique haute énergie est adaptée à ce genre
d'application, puisque la plupart des dommages cristallographiques
résiduels sont localisés en profondeur.
Après donc cette étude théorique oil nous
avons vu comment des précurseurs donnent naissance aux
nano-cavités qui vont croître sous l'influence de la
température pendant le recuit; nous avons réalisé la
simulation de cette croissance dans le matériau implanté. Une
croissance gouvernée par deux mécanismes à savoir l'Oswald
Ripening et la Migration Coalescence pour lesquels nous avons
élaboré des modèles. Les courbes obtenues pour le
mécanisme OR, nous montrent que les nano-cavités croissent
beaucoup plus vite à de hautes températures. Ces courbes nous
montrent aussi la conservation du caractère physique avant et
après recuit, et l'évolution temporelle de ces
nano-cavités respecte les lois physiques. La combinaison de ces effets
dote le matériau de propriétés extraordi-
naires pour la réalisation de divers composants
électroniques. La comparaison avec les
résultats de Evans
constitue un test important pour notre modèle. Par ailleurs, la
repro-
duction des résultats expérimentaux permettra de
déterminer les parmètres appropriés.
Les courbes obtenues, ne sont pas suffisament lisses. Ceci est
dû au fait que nous ne considérons pas la diffusion de
nano-cavités en surface, mais plutôt un nombre de lacunes et un
volume total des cavités constants.
Nous envisageons dans un avenir proche de faire des
simulations avec prise en compte de la perte de nano-cavités en surface
et la variation du nombre de lacunes de tous les mécanismes de
croissance. Une meilleure compréhension des mécanismes de
croissance permettra d'optimiser les qualités et de réduire les
coûts de production des composants électroniques.
ANNEXE
1) EQUATION MIGRATION COALESCENCE
Rappelons l'expression de l'équation de base gouvernant la
vitesse de coalescence ou de fusion des nano-cavités :
dCv
dt
= 16ðDcrC2 (3.12)
v
l'équation de croissance est réécrite en
fonction de Cv et en dérivant suivant le rayon mais avec un
volume de fusion constant;
dCv 9S dr
= (3.13)
dt 4ðr4 dt
Ensuite, en tirant Cv de cette dernière
équation et en la remplaçant dans la prémière on
obtient :
Pour le control de migration d'une cavité par le
procédé de diffusion à la surface, Nichols a tiré
la relation :
4Ù4/3
Dc = (3.15)
2ðr4
En remplaçant celle-ci dans la précédente on
obtient :
|
dr
|
6SÙ4/3
|
Ds (3.16)
|
|
|
|
=
dt
|
ðr5
|
puis, en intégrant, on arrive à :
Z r f 6SÙ4/3
= r5dr = ð Dsdt (3.17)
r0
|
= r6 - r6 0 = 36S
ð
|
(Ù)4/3 Dst (3.18)
|
Or en remplaçant Ù par son expression, on
obtient
Z r f 6S ~4ð ~4/3
rdr = ð Dsdt
3 (3.19)
r0
oil Ù est le volume d'une cavité. Ainsi donc, on
arrive à la relation :
|
r2 - r2 0 =
qui peut se mettre sous la forme
|
36S (4ð )4/3
Dst (3.20)
ð 3
|
v
r - r0 = K t (3.21)
avec K = 36S (4ð)4/3 Ds
ð 3
Bibliographie
[1] J. H. Evans, Nucl. Instr. and Meth. in Phys. Res. B 196
(2002) 125.
[2] Internet : http ://
dunham.ee.washington.edu/ee528,
janvier 2008.
[3] Hasnaa FAIK-ETIENNE, étude de l'implantation
ionique dans les miroirs multi-couches Mo/Si : applications aux optiques
diffractives, thèse de l'institut national des sciences
appliquées de TOULOUSE, 21 janvier 2005.
[4] Serge S. ZEKENG, cours de Physique des polymères en
D.E.A, Université de Yaoundé 1, semestre 1, 2007-2008.
[5] Romain DELAMARE, étude de la croissance thermique
des cavités induites par l'implantation d'helium dans le silicium,
thèse de l'université d'Orléans, 12 mai 2003.
[6] Hanan ASSAF-REDA, étude des nano-bulles induites
par implantation de gaz rares dans l'oxyde de silicium : application,
thèse de l'université d'Orléans, 26 septembre 2006.
[7] J. Grisolia, Evolution thermique des défauts
introduits par implantation ionique d'hydrogène ou d'hélium dans
le silicium et le carbure de silicium, Thèse Université Paul
Sabatier, Toulouse III (2000).
[8] figure tirée de la présentation de D. Mathiot
au 1st Yaoundé International College on Materials (7 - 11 juillet 2008
à Yaoundé, Cameroun).
[9] Frédéric BOUCARD, Modélisation de la
diffusion des dopants dans le silicium pour la réalisation de jonctions
fines, Thèse de l'Univeristé Louis Pasteur-Strasbourg I
(2003).
[10] V. M. Kaganer, K. H. Ploog, and K. K. Sabelfeld, dynamic
coalescence kinetics of facetted 2D islands, WIAS N0 1077, Berlin 2005.
[11] Herbert Schroeder, Paulo F. P. Fichtner, J. Nucl. Mater.
179-181 (1991) 1007 - 1010.
[12] Laurent OTTAVIANI, réalisation de jonction pn dans
le SiC-6H par implantation ionique d'aluminium, thèse de
l'Université d'AIX-Marseille, (1999).
[13] J. H. Evans, R. Escobar Galindo, A. Van Veen, Nucl. Instr.
and Meth. in Phys. Res. B 217 (2004) 276.
[14] http ://
www.epsic.ch/pagesperso/schneiderd/apelm/sources/solaire.php,
mars 2009.
[15] Mécanismes de germination-croissance de
nanocavités dans Si, Ruault Marie-Odile, Vincent Laetitia, J. of Applied
Physic Soumis à publication (2004)
[16] Erwan ADAM, Etudes de surfaces et d'interfaces dans le
cadre de la physique statistique, thèse de l'Université Joseph
Fourier - Grenoble I, 2 juillet 1999.
[17] E. Ntsoenzok, R. Delamare, D. Alquier, C.L. Liu , S.
Ashok, M.O. Ruault, He-induced nanocavities for the gettering of metallic
impurities in silicon, Procedings Electrochemical Society 5 (2004) 202.
[18] Servane BLANQUE, optimisation de l'implantation ionique
et du recuit thermique pour SiC, thèse de l'université des
sciences et techniques du Languedoc-Montpellier II.
[19] S. Godey, T. Sauvage, E. Ntsoenzok, H. Erramli, M.F.
Beaufort, J.F. Barbot, B. Leroy, J. Appl. Phys. 87 (2000) 2158.
[20] J. Stoemenos, Silicon on insulator (SOI), the new silicon
technology, Bulgarian journal of physics 27 (2000) 1.
[21] Xi-Qiao, Y. Huang, Mechanics of smart cut technology,
International Journal of Solids and Structures 41 (2004) 4299.
[22] Andrey Kamarou, Alexander Komarov, Pawel Zukowski,
Gettering of metal impurities to cavities formed by hydrogen and helium
implanted in silicon, Vacuum 63 (2001) 609.
[23]
www.wikipedia.org, de janvier
à septembre 2009.
| 


