Impact du déficit budgétaire sur l'inflation en RDC

III.4. Notion sur la Co-intégration

Les méthodes statistiques de l'économétrie ne sont applicables qu'à des séries stationnaires. La satisfaction au test de stationnarité des variables constitue la condition sine qua none pour l'application de la méthode des MCO. En règle générale, la régression des séries non stationnaires conduit à un vecteur d'erreur non stationnaire, c'est-à-dire ayant une variance infinie.

Cependant, lorsque les séries sont Cointégrées, le vecteur d'erreur devient stationnaire et inférence statistique demeure alors possible. Cependant, les tests de student ne suivent pas la distribution usuelle.

On appelle variables co-intégrées X_t,Y_t une combinaison de variables intégrée d'ordre « d,b », telle que le résidu de la régression : Z_t= X_t+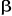Y_t¹ soit intégré d'ordre (d,b), 0<b=d.

Selon Engle et Granger (1987), lorsque deux séries sont co-intégrées CI(1,1), il est possible de dégager une représentation dynamique de court terme avec un terme de rappel Z_t-1 de long terme. C'est ce qu'on appelle « modèle à correction d'erreur ». il s'agit de la relation entre les déviations de ces deux variables par rapport à leur niveau d'équilibre de long terme.

III.4.1. Estimation du modèle à LT

Pour estimer la relation de LT les séries sont co-intégrées, il n'y a aucun problème particulier. On applique la Mco. Et si on travail sur un grand échantillon, l'estimateur de Mco possède une propriété remarquable : c'est la « super-convergence ». Cette propriété dite qu'en présence des variables co-intégrées, l'estimateur Mco du vecteur co-intégrant converge rapidement vers sa vraie valeur, et la vitesse de convergence est plus élevée que dans le cas habituel. Dans ce cas, tous les tests de vérification des hypothèses classiques sont sans importance.

- Vérification du modèle à LT par la MCO

L'équation se présente comme suit : linf=c+ldfb+lmm+lpib+ltc

Tableau n°2 : Modèle de cointégration à long terme

Variable	Coefficient	Std. Error		t-Statistic	Prob.
C	1.426746	2.936682		0.485836	0.6305
LDFB	0.211740	0.121827		1.738039	0.0921
LMM	-0.128423	0.192848		-0.665932	0.5104
LPIB	0.148796	0.069915		2.128256	0.0414
LTC	-0.208781	0.225682		-0.925114	0.3621
R²	0.372599	Variable dépendante moyenne			4.393642
R² ajusté	0.291644	Critère d'Akaike			3.998543
Somme de carré de résidu	87.04341	Critère de Schwarz			4.218476
Log de vraissemblance	-66.97377	F-statistic			4.602542
DW	0.723983	Prob(F-statistic)			.0049300

Ici, nous désirons savoir si une variable explicative dans le modèle est réellement significative, c'est-à-dire contribue à l'explication de la variable endogène.

Il convient de déterminer si son coefficient de régression est significativement différent de zéro pour un seuil de 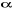= 5%. Nous constatons à ce niveau que les variables : la masse monétaire, le taux de change et la constante ne sont pas significatifs. D'où nous allons procéder à l'élimination de ces variables, en commençant par la constante qui sera suivi de la masse monétaire et en fin le taux de change. L'équation se présente comme suit :

loginf =1.426746+0.211740logdfb-0.128423logmm+0.148796logpib-66.97377logtc

Enlèvement de la constante C et le résultat est reporté dans le tableau ci-dessous:

Tableau n°3 : Enlèvement de la constante

Variable	Coefficient	Std. Error	t-Statistic	Prob.
LDFB	0.255882	0.080182	3.191248	0.0032
LMM	-0.079831	0.162903	-0.490050	0.6274
LPIB	0.143088	0.068093	2.101373	0.0436
LTC	-0.144034	0.179942	-0.800443	0.4294

Au regard de ce tableau, nous constatons qu'après enlèvement de la constante C, le coefficient de détermination passe de 37% à 36% (cfr. Annexe) et la masse monétaire n'est pas significative.

Enlèvement de la Masse monétaire

Tableau n°4 : Enlèvement de la masse monétaire

Variable	Coefficient	Std. Error	t-Statistic	Prob.
LDFB	0.217422	0.016237	13.39051	0.0000
LPIB	0.111752	0.023134	4.830602	0.0000
LTC	-0.202292	0.133515	-1.515124	0.1393

Il ressort de ce tableau qu'après enlèvement de la masse monétaire, le taux de change aussi n'est pas significatif.

Enfin, nous enlevons, le taux de change

Tableau n°5 : Enlèvement de la variable taux de change

Variable	Coefficient	Std. Error	t-Statistic	Prob.
LDFB	0.214133	0.016395	13.06088	0.0000
LPIB	0.092620	0.019750	4.689682	0.0000

A la lecture de ce tableau après enlèvement des variables qui étaient non significatives, nous disons qu'à long terme, les variables déficit budgétaire et le PIB ont un effet positif sur l'inflation. En d'autre terme, l'inflation est expliquée par ces deux variables à LT. D'où l'équation est de la forme

loginf= 0,214133logdfb+0,092620logPIB à LT

Ceci nous pousse à vérifier notre hypothèse sur l'influence de déficit budgétaire sur l'inflation.

Après analyse du modèle d'estimation, nous présentons nos tests d'hypothèses de nos variables.

Testons l'hypothèse :

4) H_O: a₄ = 0

H₁: a₄ > 0 ou a₄ < 0

5) H_o: a₅ = 0

H₁ : a₅ > 0 ou a₅ < 0

1) H_O: a₁ = 0

H₁: a₁ > o ou a₁ < 0

2) H_O: a₂ = 0

H₁ : a₂ > 0 ou a₂ < 0

3) H₀ : a₃ = 0

H₁ : a₃ > 0 ou a₃< 0

Au seuil de 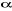= 5%, la valeur de la table de t-student à (n-k-1) dl est de 1,96, soit.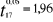

A LT nous constatons que cette estimation donne des aberrations. La masse monétaire et le taux de change ne sont pas significatifs. Comme nous le constatons sur la masse monétaire (t-calculée = 0,66 < t-table=1,96 et la probabilité = 0,51 > 0,05) et pour le taux de change (t-calculée = 0,93 < t-table=1,96 et la probabilité = 0,36 > 0,05).

Néanmoins, les paramètres liés au déficit budgétaire et au PIB présentent les signes attendus selon la théorie. Les résultats de cette estimation ne sont pas satisfaisants. Le R² n'est que de 37 %, la statistique de D-W qui est ici de 0,72. D'où nous allons procéder au modèle à correction d'erreur. Bien avant récupérons d'abord le résidu afin de tester sa stationnarité.

La vérification de la stationnarité de résidu.

Tableau n°6 : Test de stationnarité des résidus

Paramètres	t- tab.	Rés
		t-calc.
ä (3)	1,96	-0,30
ë (3)	1,96	0,41
ö (3)	-3,54	-2,86
ã (2)	1,96	0,31
ö (2)	-2,95	-3,03
ö (1)	-1,95	-3,07

Nous voyons ici que le résidu est stationnaire en niveau avec un seul retard, sans tendance ni constante.