Les déterminants de l'épargne en RDC, une analyse macroéconomique de 1960 en 2020

SECTION2. : ANALYSE ET TRAITEMENT DE DONNEES

3.2.1. Analyse de Près-estimation du modèle

a) Analyse de la stationnarité des variables

Avant de déterminer le modèle d'estimation à utiliser, il convient de faire une étude préalable des séries des différentes variables. Pour ce faire, nous utiliserons le test de racine unitaire de Dickey-Fuller Augmenté (ADF).

Le test ADF se base sur une estimation par Moindres carrés Ordinaires (MCO) de la variable par rapport à elle-même mais avec un décalage. Le test est fondé sur une hypothèse nulle correspondant à la racine unitaire (signifiant que la série n'est pas stationnaire).

Les hypothèses se présentent comme suit :

H₀ : présence de racine unitaire (la série n'est pas stationnaire) ; et

H₁ : absence de racine unitaire (la série est stationnaire)

On accepte l'hypothèse nulle si la valeur statistique du coefficient de racine unitaire est supérieure à la statistique de Dickey-Fuller au seuil critique considéré (5%) ; soit si la probabilité critique de cette valeur est supérieure à 0,05 ; dans le cas contraire, on accepte l'hypothèse alternative (dans ce cas, la série est stationnaire).

Tableau3: Résultats synthétiques du test de racine unitaire : ADF

VARIABLES	T-ADF	T-critical values à 1%	T-critical values à 5%	Probability	Level	1st level	2^endlevel
IDE	-10.11922	-3.548208	-2.912631	0.0000		**
INT	-3.842918	-3.544063	-2.910860	0.0043	*
INFL	-6.895138	-3.544063	-2.910860	0.0000	*
PIBH	-12.33379	-3.546099	-2.911730	0.0000		**
AID	-6.394660	-3.546099	-2.911730	0.0000		**
EPA	-6.018075	-3.544063	-2.910860	0.0000	*

Légende : * : à niveau ; ** : en première différence ; *** : en deuxième différence.

Source : Nous-même à partir des résultats tirés avec Eviews 12

Les résultats de ce tableau montrent à travers le test de racine unitaire de AugmentedDickey Fuller (ADF) la stationnarité en différence première de variables notamment l'investissements direct étrangers et le PIB par habitant et l'aide publique au développement tandis que le taux d'intérêt, l'inflation et l'épargne sont intégrées à niveau. Les résultats montrent par le test ADF à 1%, à 5% sont inférieures aux valeurs critiques de Mackinnon au seuil de 5%, ce qui veut dire la présence de stationnarité.

b) Etude de la causalité entre les variables

Pour vérifier la causalité entre les variables, nous avons eu à faire recourt au test de causalité bilatérale de Granger. L'hypothèse nulle de ce test correspond à l'absence de causalité d'une variable X face à une variable Y. la règle de décision est telle que l'on accepte l'hypothèse nulle si la probabilité critique du test est supérieure à 5% ; et donc, il y aura causalité entre variables si la probabilité critique est inférieure à la marge d'erreur.

Tableau4. : Résultats du test de causalité au sens de Granger

Pairwise Granger Causality Tests
Date: 10/10/22 Time: 01:10
Sample: 1960 2020
Lags: 3
NullHypothesis:	Obs	F-Statistic	Prob.
IDE does not Granger Cause EPA	58	4.94058	0.0044
EPA does not Granger Cause IDE		0.83912	0.4787
AID does not Granger Cause EPA	58	0.80927	0.4946
EPA does not Granger Cause AID		0.92918	0.4334
INFL does not Granger Cause EPA	58	4.95038	0.0043
EPA does not Granger Cause INFL		2.05968	0.1172
INT does not Granger Cause EPA	58	0.93522	0.4305
EPA does not Granger Cause INT		2.41557	0.0771
PIBH does not Granger Cause EPA	58	1.35091	0.2683
EPA does not Granger Cause PIBH		0.43918	0.7259

Source : Nous-même à partir des résultats tirés avec Eviews 12

Les résultats de ce test nous ont permis d'établir les relations suivantes :

EPARGNE

AID

PIBHAB

IDE

INTERET

INFLATION

Source : nous-même, A partir du tableau précédent

Ce schéma nous montre l'existence d'une causalité unidirectionnelle entre l'épargne et l'aide publique au développement ; entre l'épargne et le taux d'intérêt ; et entre l'épargne et le PIB par habitant. Cependant, il existe une relation bidirectionnelle entre l'épargne et l'inflation ; et l'épargne et l'investissements direct étrangers.

c) Le test de Pesaran et al. (2001)

La cointégration entre séries suppose l'existence d'une ou plusieurs relations d'équilibre à long terme entre elles. Ces relations peuvent être combinées avec les dynamiques de court terme de ces séries dans un modèle et peuvent prendre la forme d'un vecteur à correction d'erreurs ou d'un modèle à correction d'erreurs selon la forme suivante :

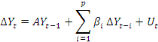
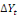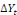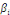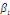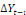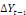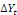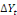Avec : = vecteur de variables stationnaires sous études (dont on explique la dynamique), = matrice dont les éléments sont des paramètres associés à  ; A= matrice de même dimension que (et r(A) représente le nombre de relations de cointégration) ; = opérateur de différence première ( kuma jonas Kibala, 2018).

Pour tester l'existence ou non de la cointégration entre série, la littérature économétrique fournit plusieurs tests ou approches. Pour notre part, nous opterons pour le test de cointégration de Pesaran et al. (2001), appelé aussi « test de cointégration aux bornes » ou « bounds test cointegration ».

Le modèle de base associé au test de cointégration par les retards échelonnés est le modèle ARDL cointégrée dont la spécification est la suivante :

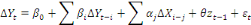
Où z_t-1 est le terme de correction d'erreur résultant de la relation d'équilibre de long terme ; c'est un paramètre indiquant la vitesse d'ajustement au niveau d'équilibre après un choc. Son signe doit être négatif et son coefficient significatif pour assurer la convergence de la dynamique vers l'équilibre à long terme. Ce coefficient varie entre -1 et 0. -1 signifie une convergence parfaite alors que 0 permet de conclure qu'il n'y pas de convergence après un choc dans le processus (Bourbonnais, 2015; Benyacoub and Mourad, 2021).

Cette relation peut aussi s'écrire comme suit :

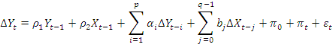
Ou

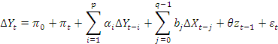
Pour vérifier l'existence d'une relation de cointégration, on recourt au test de Fisher selon les hypothèses suivantes :

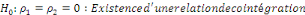
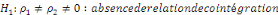
La procédure est telle qu'on devra comparer les valeurs de Fisher obtenues aux valeurs critiques (bornes) simulées sur plusieurs cas et différents seuils par Perasan et al. Et l'interprétation ou la décision se fera comme ceci :

- Si F-calculé est supérieur à la borne supérieure, il existe une relation de cointégration ;

- Si F-calculé est inférieur à la borne inférieure, il n'existe pas de relation de cointégration ; et

- Si F-calculé est compris entre les deux bornes, le test est non-concluant, aucune interprétation objective ne pourrait se faire.

Tableau 5. : Résultats du test de cointégration aux bornes

F-Bounds Test		Null Hypothesis: No levels relationship
Test Statistic	Value	Signif.	I(0)	I(1)
F-statistic	6.184653	10%	2.08	3
K	5	5%	2.39	3.38
		2.5%	2.7	3.73
		1%	3.06	4.15

Source : Nous-même à partir des résultats tirés avec Eviews 12

Les résultats du tableau ci-dessus révèlent que le F-calculé est supérieur à la borne supérieure, d'où la présence d'une relation de long terme entre les variables d'étude.

Tableau 6 : : Résultats de l'estimation du modèle ARDL à correction d'erreur

ARDL Error Correction Regression
Dependent Variable: D(LEPA)
Selected Model: ARDL(1, 4, 2, 4, 4, 1)
Case 2: Restricted Constant and No Trend
Date: 10/09/22 Time: 14:21
Sample: 1960 2020
Included observations: 57
ECM Regression
Case 2: Restricted Constant and No Trend
Variable	Coefficient	Std. Error	t-Statistic	Prob.
D(IDE)	0.048297	0.023372	2.066404	0.0463
D(IDE(-1))	-0.074656	0.030865	-2.418820	0.0209
D(IDE(-2))	-0.096981	0.028833	-3.363487	0.0019
D(IDE(-3))	-0.030675	0.023251	-1.319290	0.1956
D(INT)	0.003699	0.002843	1.301335	0.2016
D(INT(-1))	0.007839	0.003545	2.211201	0.0336
D(INFL)	-1.54E-06	1.72E-05	-0.089903	0.9289
D(INFL(-1))	-0.000181	3.86E-05	-4.693919	0.0000
D(INFL(-2))	-9.86E-05	3.80E-05	-2.591463	0.0138
D(INFL(-3))	-5.80E-05	3.78E-05	-1.533972	0.1340
D(LPIBH)	0.097809	0.231574	0.422366	0.6753
D(LPIBH(-1))	-0.113576	0.223395	-0.508409	0.6144
D(LPIBH(-2))	0.174166	0.235643	0.739109	0.4648
D(LPIBH(-3))	-0.880453	0.241488	-3.645950	0.0009
D(LAID)	0.851823	0.151485	5.623137	0.0000
CointEq(-1)*	-0.809172	0.113626	-7.121387	0.0000
R-squared	0.808855	Meandependent var		0.003920
Adjusted R-squared	0.738924	S.D. dependent var		0.698310
S.E. of regression	0.356806	Akaike info criterion		1.008673
Sumsquaredresid	5.219719	Schwarz criterion		1.582161
Log likelihood	-12.74718	Hannan-Quinn criter.		1.231550
Durbin-Watson stat	2.304767

Source : Nous-même à partir des résultats tirés avec Eviews 12

Après l'analyse et le traitement de données, les résultats révèlent dans l'ensemble avec tous les tests utilisés, le modèle est expliqué à 80,8% du coefficient de détermination. Ce qui veut dire que le modèle est globalement significatif.

Les résultats de l'estimation du modèle ARDL comme on peut le voir, c'est un modèle ARDL (1, 4, 2, 4, 4, 1) est le modèle le plus optimal parmi les 20 modèles estimés.

Interprétation du modèle

a) La dynamique de court terme

EPARGNE = - 0.074*IDE (-1) - 0.096*IDE (-2) -0.003*INT (-1) -0.0001*INFL(-1) -0.00009*INFL(-2)-0.88*PIBH(-1)

Il ressort à court terme pour ce modèle :

- Un hause de 100% des IDE décalé à la 1^ère période entraine une baisse de 7% l'épargne courante ;

- Un hause de 100% des IDE décalé à la 2^ème période entraine une baisse de 9.6% l'épargne courante ;

- Un hause de 1000% du taux d'intérêt retardé à la 1^ère période entraine une baisse de 3% l'épargne courante ;

- Un hause de 1000% de l'inflation retardée à la 1^ère période entraine une baisse de 0.1% l'épargne courante ;

- Un hause de 1000% de l'inflation retardée à la 2^ème période entraine une baisse de 0.09% l'épargne courante ;

- Un hause de 100% du PIB par habitant retardée à la 3^ème période entraine une baisse de 88 % l'épargne courante.

b) La dynamique de Long terme

EPARGNE = 0.048*IDE +0.851*AID

Les effets de Long terme révèlent :

- Une augmentation de 100% des IDE entraine une hausse de 4.8% de l'épargne ;

- Une augmentation de 100% d'aide publique au développement entraine un accroissement de 85% de l'épargne.

Le coefficient d'ajustement (0.809) ou force de rappel de l'équilibre du modèle de cointégration est statistiquement significatif,ceci garantit un mécanisme de correction d'erreur dans les variations de l'épargne. D'où, l'existence d'une relation de long terme. Autrement dit, tous les déséquilibres du modèle seront corrigés dans la période qui suive au bout de 1 ans et 2 mois.