Evaluation des performances d'un design d'avion de type blended-wing-body de 100 passagers

Évaluation des performances d'un design d'avion de type blended-wing-body de 100 passagers

par

Cédric FOFFÉ NGOUFO

RAPPORT DE PROJET PRÉSENTÉ À L'ÉCOLE DE TECHNOLOGIE
SUPÉRIEURE COMME EXIGENCE PARTIELLE À L'OBTENTION DE
LA MAÎTRISE AVEC PROJET EN GÉNIE AÉROSPATIAL
M. ING.

MONTRÉAL, LE 06 AOÛT 2021

ÉCOLE DE TECHNOLOGIE SUPÉRIEURE
UNIVERSITÉ DU QUÉBEC

Cédric FOFFÉ NGOUFO, 2021

Cette licence Creative Commons signifie qu'il est permis de diffuser, d'imprimer ou de sauvegarder sur un autre support une partie ou la totalité de cette oeuvre à condition de mentionner l'auteur, que ces utilisations soient faites à des fins non commerciales et que le contenu de l'oeuvre n'ait pas été modifié.

PRÉSENTATION DU JURY

CE RAPPORT DE PROJET A ÉTÉ ÉVALUÉ PAR UN JURY COMPOSÉ DE :

M. François Morency, directeur de projet

Département de génie mécanique à l'École de technologie supérieure

M. Stéphane Hallé, membre du jury

Département de génie mécanique à l'École de technologie supérieure

REMERCIEMENTS

Ce projet n'aurait pas été parachevé sans le soutien de plusieurs personnes à qui je souhaite témoigner ma reconnaissance.

Je tiens tout d'abord à exprimer mes remerciements les plus sincères à mon directeur de projet, le Professeur François Morency pour la confiance qu'il m'a accordée et pour m'avoir suivi, guidé et aidé avec patience tout au long de ce travail.

Mes remerciements vont également à l'endroit de Kevin Ignatowicz et Velazquez Salazar du Laboratoire de Thermo-Fluide pour le Transport (TFT) de l'ÉTS, pour leur aide indéfectible durant la réalisation de ce projet.

Il n'y a pas de mots pour dire merci à ma famille, particulièrement à mon épouse et mes frères, qui m'ont soutenu et encouragé pendant tout ce temps.

Évaluation des performances d'un design d'avion de type
blended-wing-body de 100 passagers

Cédric FOFFÉ NGOUFO
RÉSUMÉ

Le Blended Wing Body (BWB) est un modèle d'avion dont le fuselage classique en forme de tube a été remplacé par un profil d'aile. Avec cette configuration, de nombreux travaux scientifiques ont montré que ces avions promettent une baisse considérable de la consommation en carburant et un impact environnemental moindre. Cependant, la plupart des travaux existants menés sur les avions de ligne de type BWB se basent prioritairement sur des versions long-courriers; pourtant, les études de marché actuelles montrent un besoin croissant de la demande d'aéronefs moyen-courrier de capacité entre 100 et 150 passagers (Velazquez, 2020). Pour cette raison, le laboratoire TFT de l'ÉTS a initié le projet de conception d'un avion régional de type BWB ayant une capacité d'emport de 100 passagers. Ainsi, dans le cadre de ses travaux sur l'analyse aérodynamique à basse vitesse du BWB, Velazquez a proposé un design initial de l'appareil, tandis que Delacroix en a étudié la stabilité. S'inscrivant dans une logique de continuité, l'objectif de ce travail était d'évaluer les performances à basse vitesse et en croisière du BWB obtenu des travaux de Velazquez (2020) et de Delacroix (2017). Les préalables à cet objectif ont été d'estimer la masse de l'avion puis de dimensionner le système de propulsion, les surfaces verticales et le train d'atterrissage.

Ainsi, à l'aide des relations semi-empiriques de prédiction détaillée de la masse des aéronefs développées par divers auteurs, la masse maximale de l'avion a été estimée à 41950 kg, soit environ 20,2% et 6,3% de moins que les prédictions réalisées par Delacroix (2017) et Velazquez (2020) respectivement. Ensuite, à l'aide de la relation de Mattingly (1987), la poussée maximale que devrait développer les moteurs a été estimée à 168 kN, soit 13,0% de moins que l'estimation faite par Velazquez (2020). Pour ce qui est du design de la surface verticale, la solution retenue a été d'opter pour un double empennage vertical placé à la queue du fuselage. La validation de ces surfaces verticales devrait faire l'objet d'une analyse de stabilité dynamique. Concernant le train d'atterrissage, la configuration de train rétractable type tricycle (tel que pour le CRJ1000) a été adoptée. Les dimensions largeur et diamètre des roues principales et de nez ont été évaluées.

Pour ce qui est des performances de l'appareil, une évaluation détaillée des distances de décollage et d'atterrissage a révélé que le BWB décollerait sur une distance de 30% moins longue que le CRJ1000 de Bombardier ou encore l'Antonov An-158. Sa distance d'atterrissage cependant reste assez proche de celle du CRJ1000. Par ailleurs, pour que l'avion puisse voler à la vitesse de 230 m/s comme exigé dans les requis du design, l'altitude de croisière idéale

VIII

serait de 13,9 km. Pour finir, le centrage des masses et l'analyse de la stabilité de l'avion a permis d'aboutir à un design stable du BWB avec les moteurs installés sous l'aile. Avec cette configuration l'avion présente une marge statique de 9,01% à MTOW, 6,12% à OEW et 10,0% à MZFW, ce qui est acceptable au regard de la réglementation de la FAA qui préconise 5% de marge statique au moins pour un avion de ligne.

Mots clés : blended-wing-body, design d'aéronefs, performances d'avion, propulsion, stabilité statique.

Performance evaluation of a 100-passenger blended-wing-body aircraft
Cédric FOFFÉ NGOUFO

ABSTRACT

The Blended Wing Body (BWB) is an aircraft model whose classic tube-shaped fuselage has been replaced by a wing profile. With this configuration, numerous scientific works have shown that these planes promise a considerable reduction in fuel consumption and a lower environmental impact. However, most of the existing work carried out on BWB type airliners is primarily based on long-haul versions; however, current market studies show a growing demand for medium-haul aircraft with capacities between 100 and 150 passengers (Velazquez, 2020). For this reason, the ETS's TFT laboratory initiated the design project for a regional BWB type aircraft with a carrying capacity of 100 passengers. Thus, as part of his work on the low-speed aerodynamic analysis of the BWB, Velazquez proposed an initial design of the aircraft, while Delacroix studied its stability. As part of a continuity logic, the objective of this work was to assess the low speed and cruising performance of the BWB obtained from the work of Velazquez (2020) and Delacroix (2017). This objective's prerequisites were to estimate the mass of the aircraft and then to size the propulsion system, the vertical surfaces and the landing gear.

Therefore, using the detailed prediction equations for the mass of aircraft developed by various authors, the maximum mass of the aircraft was estimated at 41,950 kg, which is approximately 20.2% and 6.3% less than the predictions made by Delacroix (2017) and Velazquez (2020) respectively. Then, using the relation of Mattingly (1987), the maximum thrust that the engines should develop was estimated at 168 kN, which is 13.0% less than the estimate made by Velazquez (2020). Regarding the design of the vertical surface, the solution adopted was to opt for a vertical double tail unit placed at the tail of the fuselage. The validation of these vertical surfaces should be subjected to a dynamic stability analysis. Regarding the landing gear, the tricycle type retractable gear configuration (such as for the CRJ1000) was adopted. The width and diameter dimensions of the main and nose wheels were evaluated.

As for the aircraft's performance, a detailed assessment of take-off and landing distances revealed that the BWB would take off on a 30% shorter distance than Bombardier's CRJ1000 or the Antonov An-158. Its landing distance, however, remains fairly close to that of the CRJ1000. Furthermore, for the aircraft to fly at a speed of 230 m / s as required in the design specification, the ideal cruising altitude would be 13.9 km. Finally, weight centering and analysis of the aircraft's stability resulted in a stable design of the BWB with the engines installed under the wing. With this configuration, the aircraft has a static margin of 9.01% at

X

MTOW, 6.12% at OEW and 10.0% at MZFW, which is acceptable with regard to FAA regulations which recommend a 5% margin static at least for an airliner.

Keywords: blended-wing-body, aircraft design, aircraft performance, propulsion, static stability.

TABLE DES MATIÈRES

INTRODUCTION 1

CHAPITRE 1 REVUE DE LA LITTÉRATURE 3

1.1. Le BWB : Concept et évolution 3

1.1.1. Concept d'avion Blended Wing Body 3

1.1.2. Prototypes d'avions Blended Wing Body 5

1.2. Présentation du design de Blended-Wing-Body étudié 13

1.2.1. Paramètres critiques et de conception 13

1.2.2. Géométrie de l'avion 14

1.2.3. Résumé des performances de l'aéronef 15

1.2.4. Masse des précédents designs de l'avion 16

CHAPITRE 2 MÉTHODOLOGIE DE PRÉDICTION DE LA MASSE ET DES

PERFORMANCES DU BWB 19

2.1. Requis de la mission 19

2.1.1. Segment de mission à satisfaire par le BWB 19

2.1.2. Caractéristiques attendues de l'avion 20

2.2. Méthodologie de prédiction détaillée de la masse de l'avion 21

2.2.1. Algorithme de calcul de la masse du BWB 21

2.2.2. Prédiction de la masse à vide de l'avion 23

2.3. Dimensionnement du groupe de propulsion 36

2.3.1. Poussée maximale des moteurs 36

2.3.2. Poids et dimensions des moteurs 38

2.3.3. Altitude de vol au maximum de distance 39

2.4. Design de la surface verticale et du train d'atterrissage 40

2.4.1. Design de l'empennage vertical 40

2.4.2. Design du train d'atterrissage 45

2.5. Estimation du coefficient de trainée à portance nulle du BWB 48

2.5.1. Inventaire des sources de trainée 48

2.5.2. Estimation du coefficient de trainée parasite d'un élément 49

2.6. Estimation des performances de l'avion 52

2.6.1. Estimation des distances de décollage et d'atterrissage 52

2.6.2. Performance en montée et en descente 58

2.6.3. Facteur de charge et domaine de vol de l'avion 60

2.7. Équilibre et stabilité de l'avion 61

2.7.1. Notions de stabilité d'un avion 61

2.7.2. Marge statique et conditions de stabilité 62

2.7.3. Coefficient de moment et équilibre de l'avion 63

CHAPITRE 3 RÉSULTATS ET DISCUSSIONS 69

3.1. Résultats de l'évaluation de la masse du BWB 69

3.2. Coefficient de trainée à portance nulle du BWB 72

XII

3.3. Performance de la propulsion 74

3.3.1. Altitude de croisière pour une distance maximale 74

3.3.2. Poussée requise et poussée disponible en croisière 75

3.3.3. Performance et dimension des moteurs 76

3.4. Caractéristiques et positionnement des surfaces verticales 77

3.5. Type et dimensions du train d'atterrissage 80

3.6. Performances au décollage et à l'atterrissage 81

3.7. Performances en montée et en descente 83

3.7.1. Performances pendant la montée du BWB 83

3.7.2. Performances pendant la descente 84

3.8. Facteur de charge et domaine de vol du BWB 84

3.9. Synthèse des spécifications générales du BWB 86

CHAPITRE 4 CENTRAGE ET STABILITÉ DU BWB 89

4.1. Centrage des masses du BWB 89

4.1.1. Méthodologie de détermination du centre de masse de l'avion 89

4.1.2. Détermination du centre de gravité du BWB 90

4.1.3. Positionnement du centre de gravité sur l'avion 93

4.2. Point neutre et stabilité statique du BWB 94

4.2.1. Détermination du point neutre du BWB 94

4.2.2. Analyse de la stabilité statique du BWB 103

CONCLUSION 113

LISTE DE RÉFÉRENCES BIBLIOGRAPHIQUES 125

LISTE DES TABLEAUX

Page

Tableau 1.1 : Caractéristiques de quelques BWB conçus et testés 12

Tableau 1.2 : Paramètres critiques du BWB (Velazquez, 2020) 13

Tableau 1.3 : Paramètres géométriques du BWB (Velazquez, 2020) 15

Tableau 1.4 : Paramètres aérodynamiques du BWB (Velazquez, 2020) 16

Tableau 1.5 : Performances en croisière du BWB (Velazquez, 2020) 16

Tableau 1.6 : Performance à basse vitesse du BWB (Velazquez, 2020) 16

Tableau 1.7 : Masse détaillée du BWB, prédite par Delacroix (2017) et Velazquez (2020) 17

Tableau 2.1 : Exigences de la mission (Velazquez, 2020) 20

Tableau 2.2 : Valeurs typiques des fractions de masse par segment (Raymer, 2006) 21

Tableau 2.3 : Références du calcul détaillé de la masse de l'avion 24

Tableau 3.1 : Prédiction de masse détaillée du BWB 70

Tableau 3.2 : Répartition de la masse du BWB 71

Tableau 3.3 : Synthèse des résultats de calcul du coefficient de trainée à portance nulle 73

Tableau 3.4 : Vitesses caractéristiques du BWB en croisière 75

Tableau 3.5 : Performances des moteurs du BWB (turbosoufflante) 76

Tableau 3.6 : Poids et dimensions d'un moteur 77

Tableau 3.7 : Données du design 78

Tableau 3.8 : Résultats du design de la surface verticale 78

Tableau 3.9 : Dimensions des roues du train d'atterrissage 81

Tableau 3.10 : Données de calcul des distances de décollage et d'atterrissage 81

Tableau 3.11 : Distances de décollage et d'atterrissage du BWB 82

XIV

Tableau 3.12 : Synthèse des caractéristiques générales du BWB 86

Tableau 4.1 : Localisation du centre de gravité du BWB (moteurs à l'arrière du fuselage) 92

Tableau 4.2 : Données de paramètres géométriques de l'avion 99

Tableau 4.3 : Localisation des centres aérodynamiques du corps central et de l'aile

extérieure 100

Tableau 4.4 : Droites de portance et point neutre du BWB 101

Tableau 4.5 : Marge statique du BWB (moteurs à l'arrière du fuselage) 104

Tableau 4.6 : Coefficient de moment du BWB (moteurs à l'arrière du fuselage) 104

Tableau 4.7 : Localisation du centre de gravité du BWB (moteurs sous l'aile) 107

Tableau 4.8 : Marge statique du BWB (moteurs sous l'aile) 108

Tableau 4.9 : Coefficients de moment du BWB (moteurs sous l'aile) 109

LISTE DES FIGURES

Page

Figure 1.1 : Northrop YB-35, bombardier long-courrier (Rose, 2010) 6

Figure 1.2 : Bombardier furtif B-2A Spirit (Rose, 2010) 7

Figure 1.3 : Géométrie de base du Boeing BWB-450 (Liebeck, 2004) 8

Figure 1.4 : Prototype BWB X-48B (Gibbs, 2017) 9

Figure 1.5 : Prototype BWB X-48C (Creech et al, 2013) 10

Figure 1.6 : Prototype BWB AC 20.30 (Thomas et al, 2013) 11

Figure 1.7 : Prototype du BWB MAVERIC de Airbus (MAVERIC, 2020b) 12

Figure 1.8 : Sections finales du BWB (Velazquez, 2020) 14

Figure 1.9 : Configuration de la cabine (Velazquez, 2020) 15

Figure 2.1 : Segment de la mission (adapté de Torenbeek, 2013) 20

Figure 2.2 : Vue en plan de la géométrie simplifiée du BWB (Bradley, 2004) 26

Figure 2.3 : Procédure de design la surface verticale (adapté de Sadraey, 2012) 42

Figure 2.4 : Paramètres d'empennage vertical (Sadraey, 2012) 43

Figure 2.5 : Positionnement longitudinal du train d'atterrissage par rapport au centre de

gravité (Howe, 2000) 46

Figure 2.6 : Positionnement transversal et vertical du train d'atterrissage par rapport au centre

de gravité (Howe, 2000) 46

Figure 2.7 : Schéma d'illustration des phases de décollage (Corke, 2003) 53

Figure 2.8 : Schéma d'illustration des phases d'atterrissage (Corke, 2003) 56

Figure 2.9 : Variation du coefficient de moment avec l'angle d'attaque (cas stable) 64

Figure 3.1 : Altitude requise en croisière en fonction de la vitesse 74

Figure 3.2 : Courbe Poussée-Vitesse du BWB 75

XVI

Figure 3.3 : Vue multiple du BWB, moteurs en arrière du fuselage 79

Figure 3.4 : Vue de dessus du BWB, moteurs et surfaces verticales placés 80

Figure 3.5 : Courbe de variation du taux de montée du BWB 83

Figure 3.6 : Courbe de variation du taux de descente du BWB (moteurs éteints) 84

Figure 3.7 : Diagramme V-n du BWB, à altitude de croisière 85

Figure 4.1 : Positionnement du centre de gravité du BWB 93

Figure 4.2 : Modèle simplifié du bilan des forces appliquées à un BWB 94

Figure 4.3 : Localisation des centres aérodynamiques du corps central et de l'aile 96

Figure 4.4 : Droite de portance du BWB 102

Figure 4.5 : Comparaison entre les droites de portance analytique et CFD du BWB 103

Figure 4.6 : Variation du coefficient de moment du BWB (moteurs à l'arrière du fuselage)

105

Figure 4.7 : Variation du coefficient de moment du BWB (moteurs sous l'aile) 109

Figure 4.8 : Vue isométrique du design final du BWB 110

Figure 4.9 : Vues de face et de gauche du design final du BWB 111

LISTE DES ABRÉVIATIONS, SIGLES ET ACRONYMES

2D Deux dimensions

3D Trois dimensions

AR Arrière

AV Avant

BFL Balanced Field Length

BPR Bypass Ratio

BWB Blended-Wing-Body

CAD Computer Aided Design

CB Centerbody

CFD Computional Fluid Dynamics

CG Center of Gravity

ÉTS École de Technologie Supérieure

FAA Federal Aviation Administration

FAR Federal Aviation Regulations

ISA International Standard Atmosphere

LE Leading Edge

MAC Mean Aerodynamic Chord

MAVERIC Model Aircraft for Validation and Experimentation of Robust Innovative Controls

MEW Maximum Empty Weight

MFW Maximum Fuel Weight

MLW Maximum Landing Weight

MTOW Maximum Take-Off Weight

MZFW Maximum Zero-Fuel Weight

NACA National Advisory Comity for Aeronautics

OEW Operating Empty Weight

OW Outer Wing

PAX Passagers

RAC Règlement de l'Aviation Canadien

XVIII

RANS Reynolds Averaged Navier-Stokes

SL Sea Level

SM Static Marge

TAW Tube-And-Wings

TFT Laboratoire de Thermofluide pour le Transport

TOL Take-off and Landing

TSFC Thrust Specific Fuel Consumption

TW Transition Wing

VELA Very Efficient Large Aircraft

LISTE DES SYMBOLES ET UNITÉS DE MESURE Pente de portance du profil d'aile (2D) [rad^-1]

Angle d'attaque [deg ou rad]

Angle d'incidence à portance nulle [deg ou rad]

Allongement [-]

Envergure de l'aile [m]

Corde de l'aile [m]

Corde moyenne aérodynamique [m]

Coefficient global de traînée (3D) [-]

Coefficient de trainée du profil d'aile (2D) [-] Coefficient de traînée à portance nulle (3D) [-]

Coefficient de friction de la plaque plane [-] Coefficient global de portance (3D) [-]

Coefficient de portance du profil d'aile (2D) [-] Pente de portance de l'aile complète (3D) [rad^-1] Dérivée du coefficient de portance par rapport à l'angle d'attaque [-] Coefficient global de portance maximal (3D) [-]

C _{l max}

Coefficient de portance maximal du profil d'aile (2D) [-]

C _{m 0}

_CM

CM ? _Cm ?

_D

_CV

Coefficient de moment à portance nulle [-]

ou Coefficient global de moment [-]

ou Dérivée du coefficient de moment par rapport à l'angle d'attaque [-]

Coefficient de volume d'empennage vertical [-] Résultante des forces de trainée[N]

XX

_RC

Endurance [s]

_1D Coefficient d'Oswald [-]

Facteur de forme [-]

Facteur de structure-usine (à vide) [-]

Facteur de structure opérationnel [-]

Accélération de la pesanteur [m/s²]

Gradient de montée [-] Angle de monté [deg]

Angle de descente [deg]

Altitude[m]

Coefficient d'efficacité d'envergure [-] Marge statique [-]

? Résultante des forces de portance [N]

Finesse [-]

_Re

Angle de flèche [deg ou rad]

Effilement [-]

Longueur entre les quarts de corde de l'aile extérieure et de l'empennage vertical [m]

ou Nombre de Mach [-]

Moment [Nm]

Coefficient de friction de la piste [-] Facteur de charge [-]

Facteur d'interférence [-]

Rayon d'action [m] Taux de montée [m/s] Taux de descente [m/s]

Nombre de Reynolds sur la longueur caractéristique [-]

Masse volumique de l'aire [kg/m3]

XXI

h Surface [m²]

Surface de référence ou surface alaire [m²]

Surface mouillée [m²]

Force de poussée [kN]

Épaisseur relative du profil d'aile [-]

Ratio poussée/poids [-]

Vitesse [m/s]

Viscosité cinématique [m²/s] Poids ou masse [N, kg ou lb] Charge alaire [kg/m²]

Coordonnée sur l'axe longitudinal de l'avion [m]

LISTE DES INDICES PARTICULIERS

ac Centre aérodynamique

bwb Blended-Wing-Body

cg Centre de gravité

climb Montée

cr Croisière

des Descente

eng Moteur (engine)

fus Fuselage

LE Bord d'attaque

main Principal

max Maximum

min Minimum

np Point neutre

r ou root Racine

ref Référence
stall ou s Décrochage

t ou tip Extrémité

V ou VT Empennage vertical

INTRODUCTION

Depuis les années 1945 avec l'apparition des appareils tels que le Lockheed Constellation, le Douglas DC-6, Vickers Viscount ou encore le de Havilland Comet, la forme en « tube et aile (TAW) » des avions de ligne n'a quasiment pas changé (Reist et al, 2013). Toutefois, avec l'évolution de la recherche dans les domaines aéronautique et spatial à l'instar de l'aérodynamique, du calcul des structures, de l'aéroélasticité et de l'informatique, ces appareils n'ont cessé d'être améliorés. De manière spécifique, les améliorations de performances des avions de ligne conventionnels sont venues de modifications apportées à la conception aérodynamique (utilisation d'ailettes et de profils aérodynamiques supercritiques), à l'utilisation de matériaux hautes performances et à la construction des moteurs économes en carburant (Reist et al, 2013). Cependant, bien que les concepteurs d'avions TAW s'appuient sur le retour d'expérience acquis pendant de décennies de recherche sur cette configuration, il est aujourd'hui peu probable que des gains significatifs puissent être obtenus, à moins que des technologies radicalement nouvelles ne soient utilisées (van et al, 2014). Les constructeurs aéronautiques et la communauté scientifique réfléchissent donc à de nouvelles configurations d'aéronefs à l'instar des avions à fuselage intégré, plus connus sous le nom de Blended Wing Body (BWB). Cette configuration d'avion présente une efficacité aérodynamique élevée et des caractéristiques respectueuses de l'environnement; c'est la raison pour laquelle elle est généralement considérée comme l'une des configurations présentant le plus de potentiel pour la nouvelle génération d'avions civils (Liebeck, 2004 ; Okonkwo, 20016).

Dans l'optique d'apporter une contribution à la recherche sur les BWB, un projet de conception d'un avion de ligne moyen-courrier à fuselage intégré a vu le jour au département de génie mécanique de l'École de Technologie Supérieure, avec les travaux de Velazquez (2020) et Delacroix (2017). Ces travaux ont conduit à l'obtention des premiers designs conceptuels de l'avion, ainsi qu'à la détermination de ses caractéristiques aérodynamiques (coefficient de traînée à portance nulle, coefficient de portance, etc.). Faisant suite aux travaux de ces derniers, ce projet a pour objectif de compléter le design de l'avion d'une part et d'évaluation ses performances à haute et à basse vitesse d'autre part. Spécifiquement, le projet consistera à :

2

déterminer la masse détaillée de l'appareil, dimensionner le groupe de propulsion, dimensionner les surfaces verticales et le train d'atterrissage, estimer les distances de décollage et d'atterrissage, évaluer les performances en montée et en descente, déterminer le facteur de charge et le domaine de vol, analyser la stabilité de l'appareil pour finir.

Afin de parachever les objectifs précédents, le présent travail sera organisé en quatre chapitres s'articulant comme suit :

Le chapitre 1 réservé à la revue de la littérature permettra de présenter le concept de Blended-Wing-Body (BWB), sa genèse et son évolution. Par la suite le design du BWB objet de ce projet sera présenté. Le chapitre 2 intitulé « méthodologie de prédiction de la masse et des performances du BWB » sera réservé à la présentation de toutes les méthodes et démarches utilisées dans ce travail pour estimer la masse de l'avion, dimensionner le groupe de propulsion et l'empennage vertical d'une part, et d'autre part évaluer les performances de l'appareil à basse et à haute vitesse au regard de la mission et des requis à satisfaire. Le chapitre 3 sera réservé à la présentation et la discussion des résultats de l'estimation de la masse de l'avion, du design du groupe de propulsion et des surfaces verticales, puis de l'évaluation des performances de l'appareil en comparaison avec les avions existants. Le chapitre 4 pour finir traitera du centrage des masses et de l'analyse de la stabilité statique de l'appareil, avec les moteurs, les surfaces verticales et le train d'atterrissage positionnés. Par la suite, les dessins du design actualisé de l'avion seront présentés et commentés.

CHAPITRE 1

REVUE DE LA LITTÉRATURE

Le BWB (Blended Wing Body) est un concept d'avion dit à fuselage intégré, de par le fait que contrairement aux avions classiques à tube et aile, son fuselage est une aile à part entière qui contribue à générer de la portance. Ce chapitre a pour objectif de présenter les travaux antérieurs sur les avions à fuselage intégré, afin de guider et de positionner le design du BWB objet de ce travail. Ainsi, la première partie du chapitre sera réservée à la présentation du concept de BWB ainsi que son évolution. La seconde partie quant à telle sera réservée à la présentation du design de BWB faisant l'objet de ce projet.

1.1. Le BWB : Concept et évolution

Le BWB fait partir de la grande famille des avions dépourvus d'empennage. Il est assimilable à une aile volante, où l'épaisseur relative de la partie centrale a été maximisée afin de permettre un volume important de charge utile.

1.1.1. Concept d'avion Blended Wing Body

Le concept d'avion Blended Wing Body (BWB) a été développé dans le but de produire un avion respectueux de l'environnement et économiquement plus rentable que les avions classiques à tube et aile. En effet, les BWB promettent d'offrir des avantages aérodynamiques importants comparativement aux avions classiques, ce qui leur confère une réduction significative de la consommation en carburant, avec une capacité d'emport plus importante. (Liebeck, 2004). Le BWB a une signature à faible bruit, car il ne nécessite pas de volets ou d'empennage pour le contrôle du tangage, ce qui élimine le besoin de dispositifs hypersustentateurs au décollage et à l'atterrissage (Okonkwo, 2016).

L'une des publications les plus importantes sur la conception de l'avion BWB est certainement celle de Liebeck (2004). Il a travaillé sur le concept de BWB dans la société McDonnell

4

Douglas initialement, puis l'a développé ultérieurement dans ses travaux avec la NASA et Boeing conjointement.

Les avantages aérodynamiques du BWB viennent du fait que son fuselage et son aile sont intégrés afin d'obtenir un rapport de surface mouillée/volume moindre, et donc une réduction de la trainée d'interférence. Cela réduit la traînée totale et fournit une finesse L/D plus élevée en croisière par rapport à la configuration conventionnelle (Wan et al, 2010).

De même, Liebeck (2004) a comparé l'impact de la réduction de la surface mouillée sur le coefficient de portance d'un BWB de 800 passagers et d'un avion à tubes et aile conventionnel de capacité similaire. Il a montré que par rapport à un avion conventionnel, le BWB permet d'obtenir une réduction d'environ de 33 % de la surface mouillée. Ce qui a pour effet direct de réduit la traînée de l'avion, augmentant par conséquent la finesse L/D de 10 à 15 % par rapport à une configuration conventionnelle tubes et aile.

Ainsi, de par sa configuration unique et ses avantages probables, le BWB est bien adapté au rôle d'avion de ligne à longue portée et à grande capacité respectueux de l'environnement. Cependant, les problèmes de contrôle et de stabilité, de pressurisation de la cabine et de qualité de pilotage de l'avion entre autres, doivent être résolus (Okonkwo, 2016).

Contraintes de design des BWB (Liebeck, 2004)

Dans ses travaux sur les BWB, Liebeck (2004) a énuméré un ensemble unique d'exigences auxquelles doit satisfaire la conception de l'appareil. Quelques de ces exigences sont présentées dans les lignes qui suivent.

· Exigence de volume

Afin de garantir un espace suffisant pour accueillir les passagers, la cargaison et les systèmes de l'avion, le rapport épaisseur-corde maximum du profil d'aile constituant le corps central doit être de l'ordre de 17% au moins (Liebeck, 2004).

· Angle du pont en croisière

Étant donné que le corps central du BWB inclut la cabine passagers, son profil aérodynamique doit être choisi de sorte que ce dernier génère de la portance nécessaire à un angle d'attaque compatible avec les exigences d'angle de pont de la cabine, généralement inférieur à 3 degrés

5

(Liebeck, 2004). Au vu de cette exigence, Liebeck (2004) suggère l'utilisation d'un carrossage arrière positif sur les profils aérodynamiques du corps central.

· Équilibrage

Lorsque le centre de pression aérodynamique coïncide avec le centre de gravité et que toutes les surfaces de contrôle de bord de fuite sont carénées, le BWB est considéré comme équilibré, à la condition de croisière nominale (Liebeck, 2004). Pour ce qui est de la stabilité statique positive de l'avion, Liebeck (2004) recommande que le moment de tangage à piquer soit minimisé, afin de limiter l'utilisation d'un carrossage arrière positif et des conflits avec l'exigence d'angle de pont précédente.

· Vitesse et attitude d'approche à l'atterrissage

Pour les avions de type BWB, Liebeck (2004) affirme que la déviation de la surface du bord de fuite est définie par les exigences d'assiette plutôt que par la portance maximale. C'est la raison pour laquelle le coefficient de portance maximum (et par conséquent la charge alaire) d'un BWB sera inférieur à celui d'un avion de configuration conventionnelle. Par ailleurs, comme les BWB n'ont pas de volets, leur coefficient de portance maximum ne pourra qu'être atteint à un angle d'attaque relativement grand ; par conséquent, l'assiette de vol pendant l'approche sera proportionnellement élevée.

1.1.2. Prototypes d'avions Blended Wing Body

Les avions de type Blended Wing Body ont été développés pour la première fois il y a plusieurs décennies, à l'instar du XB-35, du YB-35 et du YB-49 développés pendant la seconde guerre mondiale pour l'armée américaine, ou encore le célèbre bombardier furtif B-2A Spirit développé pendant la guerre froide (Rose, 2010). Cette section présente de manière chronologique quelques BWB ayant été conçus et testés.

· Les XB-35 & YB-35

Les Blended Wing Body XB-35 et YB-35 étaient des bombardiers expérimentaux développés pendant la Seconde Guerre mondiale par la compagnie Northrop Corporation, pour l'armée de l'air américaine. Le XB-35 a effectué son premier vol en juin 1946 pour un voyage de 45

6

minutes de Hawthorne en Californie, à Muroc Dry Lake, sans incident (Rose, 2010). L'avion était propulsé par quatre moteurs à hélices contrarotatives. Bien que les moteurs du XB-35 étaient peu fiables, cet avion a apporté un retour d'expérience important, dans la conception des bombardiers à ailes volantes. Le YB-35 est une version évoluée du XB-35 où les moteurs à hélices contrarotatives ont été remplacés par des moteurs à hélices à rotation unique Pratt & Whitney R-4360 de puissance unitaire 2200 kW (Rose, 2010). Le YB-35 a effectué son premier vol d'essai le 15 mai 1948, puis le projet fut abandonné en juillet 1949 (Rose, 2010).

Figure 1.1 : Northrop YB-35, bombardier long-courrier (Rose, 2010)

· Northrop Grumman B-2A Spirit

Le Northrop B-2A Spirit est l'un des plus célèbres avions furtifs existants. Développé par l'avionneur américain Northrop durant la guerre froide, le B-2A Spirit est un bombardier de l'US Air Force (USAF) . Présenté comme le plus performant au monde dans sa catégorie, le B-2A Spirit est propulsé par quatre turboréacteurs General Electric F118 avec une poussée unitaire de 77 kN (Rose, 2010). Cet avion a une envergure de 52,43 mètres et une longueur de 21,03 mètres. Sa masse à vide est comprise entre 45 360 et 49 900 kg, pour une charge maximale théorique d'environ 35 tonnes de bombes et missiles divers disposée dans deux soutes (Rose, 2010). Le B-2A Spirit a effectué son vol inaugural en juillet 1989, et le premier avion opérationnel a été réceptionné par l'USAF fin 1993.

·

7

Figure 1.2 : Bombardier furtif B-2A Spirit (Rose, 2010)

Le Boeing BWB-450

En 1988, la NASA et McDonnell Douglas Corporation (maintenant Boeing Corporation) ont mis sur pieds un projet visant à effectuer une étude approfondie de la configuration BWB. Cette étude consistait à développer et comparer un nouvel avion de transport subsonique aux technologies avancées, avec un rayon d'action de 7000 nm et pouvant transporter 800 passagers à 0,85 Mach (Liebeck, 2004). L'étude a abouti sur une configuration d'avion BWB et, suite aux résultats obtenus, Boeing a lancé une seconde étude pour la conception préliminaire d'un avion de transport BWB ayant une capacité de 450 passagers (Liebeck, 2004). Des recherches expérimentales portant sur la dynamique de vol et l'aérodynamique du BWB ont abouti à une série d'essais en vol sur les modèles X-48 (A, B et C).

8

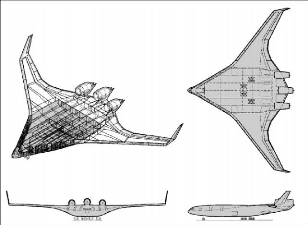
Figure 1.3 : Géométrie de base du Boeing BWB-450 (Liebeck, 2004)

· NASA-Boeing X-48

Le Boeing X-48 est une série de BWB expérimental sans pilote, développé par la NASA-Boeing et l'Air Force Research Laboratory en association, pour étudier les avantages structurels, aérodynamiques et opérationnels du concept Blended Wing Body. L'Air Force a désigné le prototype à petite échelle sous le nom de X-48B, en raison de son intérêt pour le potentiel de la conception en tant qu'avion de transport militaire multi rôle à grand rayon d'action et de grande capacité. La version modifiée mise à niveau suivante a été désignée X-48C (Larrimer et al, 2020). Le programme avait pour objectif d'en apprendre davantage sur les caractéristiques de contrôle de vol à basse vitesse du concept, appliqué aux gros avions de transport de passagers ou de fret. D'ailleurs, le X-48 est une réplique à l'échelle de 8,5% d'un avion réel (Larrimer et al, 2020 ; Gibbs, 2017). Il a été dynamiquement mis à l'échelle pour voler avec la même attitude ou presque, qu'un avion pleine grandeur. L'étude consistait également à en savoir plus sur le potentiel de la conception à obtenir une économie de carburant jusqu'à 30 % supérieure à celle des avions traditionnels (Larrimer et al, 2020). Les variantes X-48B et X-48C sont présentées dans les sections suivantes.

9

· NASA-Boeing X-48B

Le Blended Wing Body X-48B a été construit par Cranfield Aerospace au Royaume-Uni selon les spécifications de Boeing. Le prototype de sous-échelle a une envergure de 20,4 pieds, avec des ailerons verticaux proéminents, des gouvernails aux extrémités des ailes et des élevons le long des bords de fuite des ailes. L'avion est équipé de trois petits turboréacteurs, fournissant une poussée combinée maximale d'environ 150 lb, avec une masse totale de 523 lb. Le X-48B a une vitesse de pointe estimée à 118 noeuds (222 km/h), une altitude maximale d'environ 10000 pieds et une durée de vol d'environ 40 minutes (Larrimer et al, 2020). Le contrôle au sol de l'avion a commencé à la NASA Dryden à la fin 2006, et les premiers vols d'essai ont été effectués début de 2007 (Gibbs, 2017 ; Larrimer et al, 2020). Les essais visaient à caractériser le vol à basse altitude de la configuration à fuselage intégrée, y compris le contrôle de panne moteur, les caractéristiques de décrochage et les qualités de manoeuvrabilité. Le programme d'essais en vol court a été conçu pour démontrer que la nouvelle conception peut être pilotée aussi sûrement que les transports traditionnels à tube et aile.

Figure 1.4 : Prototype BWB X-48B (Gibbs, 2017)

· NASA-Boeing X-48C

Le Blended Wing Body X-48C est une version modifiée du X-48B. il a effectué son premier vol avec succès le 7 août 2012 à Edwards Air Force Base (Larrimer et al, 2020 ; Creech et al, 2013). L'avion a été conçu par Boeing, en partenariat avec la NASA. Les principales modifications apportées au modèle « C » par rapport au modèle « B » visaient à rendre l'avion plus silencieux. Les modifications de la géométrie comprenaient le déplacement des winglets de bout d'aile vers la queue de l'appareil (à côté des conduits d'échappement du moteur),

10

transformant ainsi ces derniers en deux surfaces verticales (Larrimer et al, 2020 ; Creech et al, 2013). Le corps arrière de l'avion a été allongé d'environ deux pieds vers l'arrière. Côté propulsion, l'équipe projet a remplacé les trois moteurs à réaction de 50 livres du X-48B par deux moteurs de 89 livres pour le X-48C.

En outre, le X-48C a conservé la plupart des dimensions du modèle B, avec une envergure d'un peu plus de 20 pieds et un poids avoisinant 500 livres. Sa vitesse de pointe est estimée à environ 140 mph, pour une altitude maximale de 10 000 pieds (Larrimer et al, 2020 ; Creech et al, 2013).

Au regard des différences de manoeuvrabilité du X-48C par rapport au X-48B, l'équipe du projet a apporté des modifications logicielles du système de commande de vol, afin d'adapter le domaine de vol de l'avion, en concordance aux futurs avions commerciaux BWB grandeur réelle (Larrimer et al, 2020).

Figure 1.5 : Prototype BWB X-48C (Creech et al, 2013)

· Le projet AC 20.30

Afin de stimuler les recherches sur les BWB, la Commission Européenne a soutenu d'octobre 2002 à octobre 2005 un projet baptisé VELA, qui signifie : Very Efficient Large Aircraft (Scholz, 2007). L'objectif était de concevoir un avion de ligne sous forme d'aile volante, ayant une capacité comparable à celle de l'A380. Le projet a abouti sur les designs VELA 1, VELA 2 et VELA 3 conçus par le DLR (Centre aérospatial allemand) et Airbus. Par la suite les étudiants de l'Université des sciences appliquées (UAS) de Hambourg, Département d'ingénierie automobile et aéronautique, ont travaillé sur le projet BWB A0.30. La géométrie de l'AC 20.30 était basée sur celle du VELA 2. Dans le cadre de ce projet, un prototype sans

11

pilote à l'échelle 1 :30 de l'A0.30 a été développé et construit. Puis de nombreux essais de simulations numériques en soufflerie et en vol ont permis de mieux comprendre le comportement de l'avion, ce qui a contribué à son amélioration. Ces différents essais ont permis d'obtenir une configuration stable de l'appareil (Schmidt et al, 2006).

L'A0.30 a une envergure de 3,24 m et une longueur de 2,12 m, avec une masse au décollage de 12,5 kg. L'appareil possède deux moteurs délivrant chacun une poussée de 30 N (Schmidt et al, 2006).

Figure 1.6 : Prototype BWB AC 20.30 (Thomas et al, 2013)

· Airbus MAVERIC

Lancé en 2017, le Blended Wing Body MAVERIC (Model Aircraft for Validation and Experimentation of Robust Innovative Controls) de Airbus a effectué son premier vol en juin 2019 (MAVERIC, 2020a). Le MAVERIC a été dévoilé le 11 février 2020 à Singapour. Avec ce projet, l'objectif de Airbus est de tirer parti des technologies émergentes pour être le pionnier de l'avenir du vol. L'avion a une envergure de 3,2 mètres, une longueur de 2 mètres et une superficie d'environ 2,25 m². MAVERIC présente une conception d'avion révolutionnaire, qui a le potentiel de réduire la consommation de carburant jusqu'à 20% par rapport aux avions à tube et aile conventionnels (MAVERIC, 2020a).

·

12

Figure 1.7 : Prototype du BWB MAVERIC de Airbus (MAVERIC, 2020b)

Synthèse des caractéristiques des BWB présentés

Le tableau 1.1 fournit une synthèse des caractéristiques disponibles, des principaux BWB présentés précédemment.

Tableau 1.1 : Caractéristiques de quelques BWB conçus et testés

Paramètre caractéristique	YB-35 (Rose, 2010)	B-2A Spirit (Rose, 2010)	X-48B (Larrimer et al, 2020)	X-48C (Larrimer et al, 2020)		A0.30 (Schmidt et al, 2006)	Envergure
52,5 m	52,42 m	6,4 m	6,1 m	3,2 m		Allongement
7,4	-	4,1	4,1	-		Charge alaire
220 kg/m^2	356 kg/m^2	25,3 kg/m^2	25,3 kg/m^2	6,22 kg/ m^2		Masse à vide
54 432 kg	69 717 kg	178 kg	178 kg	-		Masse maximale au décollage
95 000 kg	170 550 kg	237 kg	237 kg	12,5 kg		Puissance totale
8 800 kW	-	-	-	-		Poussée totale
-	308 kN	0,72 kN	0,79 kN	0,06 kN		Vitesse maximale
629 km/h	915 km/h	219 km/h	225 km/h	108 m/s		Rayon d'action
13 100 km	10 186 km	35 min de vol	35 min de vol	-		Plafond
12 100 m	15 240 m	3 048 m	3 048 m	-		Facteur de structure
0,573	0,409	0,751	0,751	-		Poussée/Poids
-	0,205	0,304	0,333	0,48

13

Au regard des caractéristiques présentées dans le tableau 1.1, il apparait que le B-2A Spirit, avec un facteur de structure de seulement 0,409 et un rapport poussée/poids de 0,205 est un avion aux performances avancées, en comparaison avec le YB-35, ou en encore avec les X-48B et C. Par ailleurs, le facteur de structure des BWB X-48B et X-48C semble assez élevé. Ceci pourrait s'expliquer par le fait qu'il s'agit de prototypes expérimentaux sans pilote. Ils intègrent donc certainement un nombre important d'équipements d'acquisition, de contrôle et de monitoring.

1.2. Présentation du design de Blended-Wing-Body étudié

L'avion étudié est un BWB, dont le design préliminaire et l'analyse de stabilité ont été réalisés par Velazquez (2020) et Delacroix (2017). Dans cette section, les paramètres de performance ainsi que la géométrie de l'avion seront présentés.

1.2.1. Paramètres critiques et de conception

Le tableau ci-après donne les paramètres critiques de l'avion. Ces paramètres ont été obtenus par Velazquez (2020), grâce à des analyses basses et hautes fidélités.

Tableau 1.2 : Paramètres critiques du BWB (Velazquez, 2020)

Paramètres critiques	Notation		Valeur	Finesse
	16,6		Charge alaire
	140 kg/m^2		Ratio poussée-poids
	0,441		Consommation spécifique
	0,680 lb/lb-h		Coefficient de portance maximale
	0,67

Cependant, la valeur du ratio poussée-poids de 0,441 estimée semble trop élevée, en comparaison avec les avions commerciaux de type TAW de taille similaire donc les caractéristiques sont présentées en annexe (cf. annexe 1). Sur la base des cinq avions TAW de la catégorie "avion de ligne régional" de type jet que présente cette annexe, il en ressort que le

14

rapport "poussée-poids" des avions de cette catégorie se situerait entre 0,28 et 0,36 ; donc bien moins en dessous des 0,441 estimé par Velazquez (2020).

1.2.2. Géométrie de l'avion

À l'issue de son design, Velazquez (2020) propose une géométrie optimisée de l'appareil, notamment du corps central (fuselage), de l'aile extérieure ainsi que de la jonction aile-fuselage. L'aménagement de l'espace interne de l'avion est également présenté.

· Configuration extérieure (Velazquez, 2020)

La figure 1.8 présente une vue en plan de l'avion décomposée en CB (corps central), TW (jonction corps central et aile extérieure) et OW (aile extérieure). L'axe x représente la mesure d'abscisse dans le sens de la corde à partir du bord d'attaque du profil central. L'axe y représente l'ordonnée de la demi-envergure. Le CB est caractérisé par un profil aérodynamique LA2573A à ses extrémités (y = 0m et y = 5m) tandis que le OW est caractérisé par un profil aérodynamique SC(2)-0712 à ses extrémités (y = 6,5m et y = 17,2m). La surface de référence Sref est fixée à Sref = 316 m². Il en résulte une distribution de surface de 65% à 35% entre le CB et le reste de l'aile (Sce = 0,65Sref, Sow + Tw = 0,35Sref).

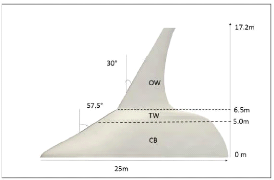
Figure 1.8 : Sections finales du BWB (Velazquez, 2020)

· Disposition cabine-soute (Velazquez, 2020)

Le corps central contient à la fois la cabine passagers et la soute, y compris le cockpit. L'angle de balayage de la baie (60°) définit le nombre maximum de sièges par rangée allant de 6 à 12.

Le tableau 1.4 montre les paramètres aérodynamiques résultant d'une analyse haute-fidélité de la géométrie (Velazquez, 2020).

15

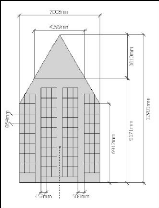
Figure 1.9 : Configuration de la cabine (Velazquez, 2020)

_{?LE, CB}

_?LE , _O

La soute contient quatre conteneurs équivalents LD3 d'une capacité maximale de volume de chargement de 20m³. Ces conteneurs LD3 sont situés à gauche et à droite de la cabine passagers, ajoutant 2 X 1,53 m à la portée du CB.

1.2.3. Résumé des performances de l'aéronef

Le tableau 1.3 présente les paramètres géométriques de l'avion que sont : l'envergure (b), la surface de référence de la forme en plan (Sref), l'allongement (AR), l'angle de flèche, la corde

à la racine (Croot), la corde moyenne aérodynamique (), l'angle de vrille (??) et l'effilement (A).

Tableau 1.3 : Paramètres géométriques du BWB (Velazquez, 2020)

											34,4m
316m^2	3,76	57,5°	30°	25m	7,6m	16,9m	0°	0,20

16

Tableau 1.4 : Paramètres aérodynamiques du BWB (Velazquez, 2020)

^CDO	^CL,cruise	CL,max	(L D)max		(L D)cr	0,0118
0,230	0,670	16,6	15,3

Le tableau 1.5 présente l'altitude de croisière désirée Hcr, la poussée de croisière Tmax,cr, les vitesses minimales et de croisière estimées, puis le rayon d'action maximal Rmax du BWB, suite à l'évaluation de Velazquez (2020).

Tableau 1.5 : Performances en croisière du BWB (Velazquez, 2020)

Tm ,Hp	H raise	Vcr,min	Ver		Rinax	34,3 kN
14,3 km	115 m/s	230 m/s	2500 km

Le tableau 1.6 présente les valeurs de performance à basse vitesse, à savoir la poussée maximale au niveau de la mer Tmax, sL, l'altitude de roulage au sol HTOL, les vitesses de décrochage et d'approche estimées à HTOL, et la longueur de piste minimale requise au décollage.

Tableau 1.6 : Performance à basse vitesse du BWB (Velazquez, 2020)

^Tmax,sL	HTOL	stall	^VapProci		^Srun	193 kN
0 m	52 m/s	68 m/s	1,41 km

1.2.4. Masse des précédents designs de l'avion

Dans le cadre de leurs travaux respectifs, Delacroix (2017) et Velazquez (2020) ont chacun fait une estimation détaillée de la masse du BWB, sur la base des mêmes requis présentés au tableau 2.1. Le tableau 1.7 présente les évaluations détaillées de la masse du BWB, tirées leurs travaux.

17

Tableau 1.7 : Masse détaillée du BWB, prédite par Delacroix (2017)
et Velazquez (2020)

Éléments	Masse de l'avion Delacroix (2017)		(kg) Velazquez (2020)	Corps central
4672	6442		Aile
889	2575		Equipment
4449	6592		Train d'atterrissage principal
2545	382		Train d'atterrissage avant
449	2167		Propulsion
3112	4667		Masse à vide estimée
16116	n/a		Pénalité
13193	n/a		Total Masse à vide
29310	22825		Carburant dans le corps central
	4838
10994			Carburant dans l'aile
	4838		Total carburant
10994	9677		Équipage
467	467		Passagers (en cabine)
9340	9340		LD3
2415	2415		Totale charge utile
12222	12222		Masse totale maximale au
			décollage (MTOW)
52526	44724

Pour le même avion et avec les mêmes requis de mission, on observe une différence significative entre les prédictions de masse présentée par Delacroix (2017) et celle présentée par Velazquez (2020). En effet la masse totale au décollage de l'avion prédite par Delacroix (Delacroix, 2017) est de 17,5% supérieure à celle prédite par Velazquez (Velazquez, 2020).

À la vue de cet écart entre les deux estimations, la masse du design initial de l'avion sera prise comme étant la moyenne entre les masses de design prédites par Delacroix (2017) et de Velazquez (2020).

18

Dans ce chapitre, il était question dans un premier temps de présenter le concept d'avions de type BWB en comparaison avec les avions à TAW classiques. Par la suite, quelques avions de type BWB remarquables ayant été conçus et testés ont été présentés, ainsi que leurs caractéristiques. Puis, la dernière version à date du design de BWB réalisé par Velazquez (2020) et objet de ce travail a été présenté. Ensuite, une comparaison entre la masse du design du BWB prédite par Velazquez (2020) et celle prédite par Delacroix (2017) dont les travaux étaient basés sur un design antérieur de l'avion a été effectuée. À l'issue de cette comparaison, il en est ressorti que la masse du BWB prédite par Delcroix était 17% plus grande que celle prédite par Velazquez. Au regard de cette différence tout de même significative, la suite de ce travail consistera à élaborer une méthodologie qui permettrait de prédire la masse de l'avion d'une part, puis à réévaluer ses performances d'autre part.

CHAPITRE 2

MÉTHODOLOGIE DE PRÉDICTION DE LA MASSE ET DES PERFORMANCES

DU BWB

Ce chapitre présente la démarche ainsi que les méthodes utilisées pour la détermination de la masse détaillée du BWB, le dimensionnement du groupe de propulsion, le dimensionnement des surfaces verticales et du train d'atterrissage, l'estimation des distances de décollage et d'atterrissage, l'évaluation des performances en montée et en descente, le calcul du facteur de charge et le domaine de vol, l'analyse de la stabilité de l'appareil pour finir.

2.1. Requis de la mission

Cette section présente les exigences opérationnelles auxquelles devrait satisfaire le BWB tels que : la charge utile minimale, la vitesse de croisière, le rayon d'action, l'endurance en attente et la longueur maximale de la piste.

2.1.1. Segment de mission à satisfaire par le BWB

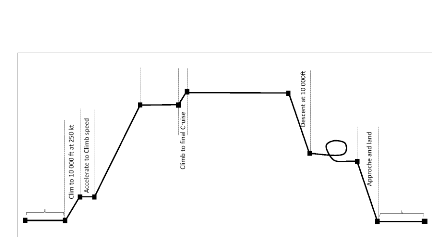
La figure 2.1 présente la mission type à laquelle le BWB devrait satisfaire. Il s'agit d'un profil type pour un vol commercial. Le carburant total doit être capable d'assurer la mission, avec une réserve minimale de 5% à l'atterrissage.

La mission commence en 0 du desserrage des freins au décollage, et se termine à l'arrêt des moteurs après l'atterrissage 11. Le carburant total emporté pour la mission doit permettre de réaliser toutes les phases de la mission à savoir : le décollage 0-1, l'accélération et la montée jusqu'à l'altitude de croisière initiale 1-4, la vitesse de croisière initiales 4-5, la montée jusqu'à l'altitude de croisière 5-6, le vol de croisière 6-7, la descente et l'attente à 10,000 pieds 7-9, la descente et la décélération pour l'approche 9-10, puis l'atterrissage à destination 10-11.

20

^{0 1}

^{10 11}

^Initial

^cruise

^Climb

^take-off

^{2 3}

^{4 5}

^{Cruise flight}

6 7

^Loiter

^reserve

Le tableau 2.2 donne les valeurs moyennes typiques des fractions de masse entre les différentes phases de la mission. Dans ce tableau, M_a représente le nombre Mach de vol.

Figure 2.1 : Segment de la mission (adapté de Torenbeek, 2013)

2.1.2. Caractéristiques attendues de l'avion

^{Taxi and}

⁸

⁹

^{Taxi from}

Le BWB doit être conçu de telle manière que ses caractéristiques opérationnelles satisfassent

aux exigences de la mission. Ainsi, le tableau 2.1 présente les requis opérationnels auxquelles

doit satisfaire l'avion.

Tableau 2.1 : Exigences de la mission (Velazquez, 2020)

Paramètre de la mission	Symbole	Unité		Valeur	Nombre de passagers
PAX	-	100		Charge utile
Wpayload	kg	11640		Équipage (5 membres)
Wcrew	kg	582		Rayon d'action
R	km	2500		Mach de croisière
Mcr	-	0,78		Longueur de piste (décollage et atterrissage)
BFL	m	2000		Endurance en attente
E	min	45

21

Tableau 2.2 : Valeurs typiques des fractions de masse par segment (Raymer, 2006)

Segment	Phase de la mission			0-1
Démarrage des moteurs, roulage et décollage	0,980		1-2
Montée à 10 000 ft à 250 kts	1,0065 - 0,0325Ma		2-3-4
Accélération jusqu'à la vitesse de seconde montée 450 kts et montée	1,0065 - 0,0325Ma		4-5
Croisière initiale 34 440 ft (10 500 m)	Équation de Breguet		5-6
Montée à 47 560 ft (14 500 m) pour le vol de croisière	0,990		6-7
Vol de croisière à 47 560 ft (14 500 m)	Équation de Breguet		7-8
Descente à 10 000 ft	0,993		8-9
Survol en attente	Équation d'endurance		9-10
Descente et approche pour atterrissage	0,993		10-11
Atterrissage	0,995

Dans les sections qui suivent, la masse maximale de l'avion au décollage (MTOW) pourra être déterminée, de manière à ce que l'avion soit capable de satisfaire la mission.

Par ailleurs, la distance parcourue par l'avion pendant la phase de croisière initiale sera assumée inférieur ou égale au 1/10ième du rayon d'action maximal, car il s'agit d'une phase assez courte permettant aux pilotes de préparer les conditions de vol de la croisière finale.

2.2. Méthodologie de prédiction détaillée de la masse de l'avion

La prédiction de la masse est une étape cruciale lors du processus de design d'un avion. Cette section présente la méthodologie utilisée pour le calcul de la masse détaillée du BWB.

2.2.1. Algorithme de calcul de la masse du BWB

L'algorithme ci-après présenté décrit succinctement la structure du programme MATLAB élaboré pour le calcul de la masse détaillée de l'avion. Étant donnée l'approche itérative de l'estimation de la masse d'un aéronef, une masse de départ est nécessaire, pour démarrer les

22

calculs. Dans le processus de design d'un avion, cette masse initiale correspondrait à la « la masse du design préliminaire ».

Pour ce travail, la masse du design préliminaire de l'avion sera prise comme étant la moyenne des masses de design obtenues par Delacroix (2017) et Velazquez (2020). Le facteur de structure en opération (OEW/MTOW) de l'avion sera pris à l'initial comme étant la moyenne des facteurs de structure opérationnels des avions de ligne régionaux de type TAW de taille comparable (cf. annexe 1).

niter = ₀

Conditions initiales

--* Définir la masse du design préliminaire de l'avion, à partir des travaux de Delacroix (2017) et de Velazquez (2020).

[kg]

[kg]

_{niter ,max}

--* Définir le facteur de structure opérationnel de l'avion, à partir des avions TAW de taille comparable (cf. annexe 1).

--* Choisir le modèle de prédiction de la masse de l'aile extérieure, parmi les modèles de Howe (200), Kundu (2019) et Torenbeek (2013).

--* Initialiser l'erreur de calcul de la masse maximale au décollage (MTOW)

--* Initialiser du nombre d'itérations de calcul

--* Définir le nombre d'itérations maximal de la boucle de calcul

End

23

Boucle de calcul de la masse de l'avion

While and ( , )

_{W W}

_{i i}

OE + pay

For

MTOW i

If

else

_{1-(1-WW)( 1} + _f + _f )

End

Calculer la masse à vide détaillée du BWB

_{LA TO ess trap}

Calculer la masse à vide opérationnelle du BWB

Erreur MTOW

MTOW i

₁ -

MTOW -

Calculer la masse maximale au décollage du BWB

Déduire la masse de carburant

Déduire le facteur de structure du BWB

Calculer l'erreur relative entre les masses maximales au décollage à i-1 et à i =

End

_i

₁

2.2.2. Prédiction de la masse à vide de l'avion

Dans toute cette rubrique, l'estimation de la masse de l'avion a été réalisée à l'aide des méthodes empiriques d'estimation de la masse des composants à l'exception de la masse de la cellule théorique du BWB où l'approche d'estimation semi-empirique de Bradley (2004) a été

24

utilisée. Le tableau ci-après présente la liste des références qui ont été utilisées pour l'estimation de la masse.

Tableau 2.3 : Références du calcul détaillé de la masse de l'avion

GROUPE	DÉTAIL DES ÉLÉMENTS		MODEL	ÉLÉMENTS STRUCTURAUX
Structure de la Cellule
	(Howe, 2000 ; Kundu, 2019 ; Torenbeek, 2013)
	(Kundu, 2019)
	Bradley (2004)
	Bradley (2004)
	Torenbeek (2013)
	Torenbeek (2013)
	Raymer (2006)
	Kundu (2019)

25

	Ensemble Fournitures (sièges, mobilier, oxygène, etc.)		Kundu (2019)	CHARGE UTILE
Passagers, y compris les bagages à main	(Corke, 2003 ; Raymer, 2006)
	Raymer (2006)
	Howe (2000)		ÉLÉMENTS OPÉRATIONNELS
Équipage (05 membres)	(Corke, 2003 ; Raymer, 2006)
	Kundu (2019)		CARBURANT
Carburant dans l'aile (50%) Carburant dans le fuselage (50%)	Déduit

2.2.2.1. Estimation de la masse du fuselage

_{0,166552 1,061158}

_W = _{K x 0,316422} ? _{MTOW x S}

_{fuse s cabine}

Le modèle de Bradley (2004) a été utilisé pour prédire la masse du fuselage. La méthode de prédiction de masse de Bradley repose sur un modèle semi-empirique implémenté dans le logiciel d'optimisation de vol (FLOPS). Ce modèle permet de déterminer la masse du corps central d'un BWB comme étant la somme de la masse du corps central avant (qui représente la partie pressurisée du fuselage) et du corps central arrière compté à partir de 70% de la corde du corps centrale, tel qu'illustré par la figure 2.2.

_MTOW

K s = ( _{5,698869 450} ) n pax

Avec ce modèle, la masse du corps central avant est donnée comme suit :

(2.1)

Avec :

.

[lb] le poids total maximum au décollage.

26

[ft²] la surface de référence de la cabine. le nombre de passagers.

La masse du corps central arrière incluant un facteur pour le nombre de moteurs supportés par le corps central est donnée par l'équation suivante :

(2.2)

Avec :

le nombre de moteurs installés sur le fuselage.

[ft²] la surface de référence de la section arrière du fuselage.

[lb] le poids total maximum au décollage. l'effilement de la section arrière du fuselage.

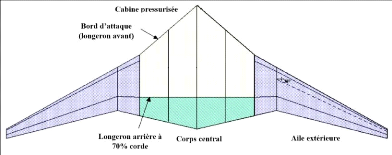
Figure 2.2 : Vue en plan de la géométrie simplifiée du BWB (Bradley, 2004)

2.2.2.2. Estimation de la masse de l'aile extérieure

Dans ce travail, l'aile extérieure du BWB sera assumée semblable à l'aile d'un avion conventionnelle. Dans la littérature, Il existe plusieurs modèles semi-empiriques permettant d'estimer la masse de l'aile d'un avion conventionnel, à l'instar des modèles de Howe (2000), de Kundu (2019) et de Torenbeek (2013).

27

· Avec le modèle de Howe, la masse de l'aile extérieure est donnée par l'équation suivante (Howe, 2000) :

[kg] (2.3)

Où :

est l'allongement de l'aile.

[m²] est la surface de référence de l'aile.

= 9x 10^-a pour les avions de type jet moyen-courrier.

est l'effilement de l'aile.

[m/s] est la vitesse de divergence de l'avion.

· Avec le modèle de Kundu, la masse de l'aile extérieure est donnée par l'équation

suivante (Kundu, 2019) :

_{W =c ?k ?k ?k ?k ?k} ?

_{wing w uc sl sp wl re}

( _{MTOW?nul)0,48?Sw,78?ARw?(1+?)0,4}

? ₁ - _{Wfuel _mass _in _wing}

? MTOW

		cos ( ) ? 0.25 ? t c		0,4

^re pour aucun moteur, 0,98 pour deux moteurs et 0,95 pour quatre moteurs (généralisé).

(2.4) Où :

_k=1

c_w = 0, 0215 pour des volets de montage standard sur l'aile.

k =1,02 pour le train d'atterrissage monté sur les ailes, sinon 1,0.

ksl =1,04 pour l'utilisation des slats.

ksp =1,01 pour un spoiler.

kwl =1,01pour un winglet (une approche généralisée consiste à avoir une taille standard).

· 28

_?V.

Avec le modèle de Torenbeek, la masse de l'aile extérieure est donnée par l'équation suivante (Torenbeek, 2013) :

Où :

_t c VT

(2.5)

[ft] une valeur de référence du modèle. [lbf/ft²] une valeur de référence du modèle.

2.2.2.3. Estimation de la masse de l'empennage vertical

Le modèle de Kundu (2019) pour l'estimation de la masse de l'empennage vertical d'un avion à réaction est donné par l'équation suivante :

_?V.

(2.6)

Avec :

pour les empennages en T, 1,2 pour les empennages médians et 1,0 pour les

empennages bas.

l'allongement de l'empennage vertical.

la surface de référence de l'empennage vertical.

l'effilement de l'empennage vertical.

l'angle de flèche de l'empennage vertical (pris au quart de corde). l'épaisseur relative du profil d'aile de l'empennage vertical.

29

2.2.2.4. Estimation de la masse des éléments internes

Estimation de la masse des surfaces de contrôles (Raymer, 2006)

Les surfaces de contrôle incluent toutes les surfaces mobiles de l'aile qui n'ont pas été incluses dans le calcul de la masse des volets. Le groupe comprend toutes les commandes internes de l'aile et les commandes des dispositifs de bord d'attaque externes.

(2.7)

Estimation de la masse du train d'atterrissage (Torenbeek, 2013)

La masse du train d'atterrissage comprenant les trains avant et arrière est donnée par la relation suivante :

(2.8)

Estimation de la masse du système de propulsion (Torenbeek, 2013)

La masse du groupe de propulsion inclut le moteur, la nacelle, le pylon, le système de carburant, système d'huile et démarreur.

( _eng ) fix

(2.9)

Avec :

le nombre de moteurs de propulsion installés.

_W

[lbf] la poussée maximale au décollage.

[lbf] l'effet d'échelle correspondant à 1 800 lbf par moteur.

Estimation de la masse des équipements/instrumentations

La masse du système d'air conditionné est donnée par l'équation suivante :

_V ?

_{0,25 pr 0,10}

_62,36 ? ? ?

_W = _N

_AirCond p ₁₀₀₀ ? W uav

? ?

_0,604 (2.10)

30

Avec :

le nombre de personnes à bord (équipage et passagers).

_N = _n

_{gen eng}

[ft³] le volume de la section pressurisée.

(lb) la masse des systèmes avioniques non installés.

La masse des systèmes avioniques s'exprime comme suit (Raymer, 2006) :

(2.11)

La masse des systèmes hydrauliques est donnée comme suit (Raymer, 2006) :

(2.12)

Avec :

le nombre de fonctions exécutées par les commandes.

[ft] la longueur totale du fuselage.

[ft] l'envergure des ailes.

La masse des systèmes électriques s'exprime comme suit (Raymer, 2006) :

W instruments = _4,509 K _r K _tp N c N _en L _f B w

0,541 ( )0,5

(2.13)

Avec :

_K = _1,0

la puissance du système électrique [KVA].

[ft] la distance du chemin de câble électrique entre générateurs-avioniques-cockpit.

le nombre de générateurs.

La masse des instruments est donnée par l'équation suivante (Raymer, 2006) :

+

(2.14)

Avec :

_r

pour les moteurs non alternatifs.

31

pour les jets.

le nombre de membres d'équipage. le nombre de moteurs.

La masse des accessoires de manutention est donnée par la relation suivante (Raymer, 2006) :

(2.15)

Où :

est la masse totale au décollage du design préliminaire.

La masse du système de dégivrage est donnée l'équation suivante (Raymer, 2006) :

KFUR =?0,07;0,08?

(2.16)

La masse de l'unité de puissance auxiliaire (APU) s'exprime comme suit (Kundu, 2019) :

(2.17)

W FUR = _{KFUR MTOW}

Où :

est un coefficient pris dans l'intervalle est la masse d'un moteur à sec.

Estimation de la masse du groupe d'ameublement et fournitures (Kundu, 2019)

Ce groupe comprend les sièges, les cuisines, le mobilier, les toilettes, le système d'oxygène et la peinture. Sa masse totale peut être estimée par la relation suivante :

(2.18)

Avec :

pour les avions de 100 passagers et plus.

32

_Wpayload

Estimation de la masse des éléments opérationnels (Howe, 2000)

Les éléments opérationnels incluent : équipage et objets personnels associés, équipements de sécurité tels que l'oxygène d'urgence et les radeaux de sauvetage, matériel de fret, eau et nourriture.

n pax

(2.19)

Avec :

le nombre des membres d'équipage.

le nombre de passagers.

le facteur des éléments opérationnels pour les avions moyen-courriers.

Estimation de la charge utile payante

La charge utile est la capacité nette d'emport d'un aéronef. Pour un avion de transport, la charge utile comprend les bagages, la cargaison, les passagers, les bagages, et d'autres charges prévues (Sadraey, 2013). Dans le cas d'un avion de passagers, le poids des passagers doit être déterminé. Le poids moyen d'un passager avec bagage en main peut être pris à 180 livres. De plus, chaque passager a droit à une franchise de bagages 40 à 60 livres en soute, pour les trajets interrégionaux (Corke, 2003 ; Raymer, 2006). Les bagages en soute sont mis dans deux conteneurs de type LD-3. Chacun de ces conteneurs a une masse à vide de 463 lb (210 kg). L'équation ci-après donne l'expression de la charge utile payante, pour le BWB.

_{m= 180}

= ₅₀

(2.20)

Avec :

[lb] la masse totale de la charge utile.

le nombre de passagers.

[lb] la masse d'un passager avec bagage en main.

_{m= 463}

[lb] la franchise de bagages par passager pour les avions régionaux.

_ncont

le nombre de conteneurs en soute.

_cont

[lb] masse à vide d'un conteneur LD-3.

33

Masse à vide de l'avion

Une fois que la masse de toutes les sous-composantes de l'avion a été calculée, la masse à vide se déduit par sommation comme présentée dans le tableau 2.3 précédent.

(2.20)

Estimation du facteur de pénalité de la masse totale (Kundu, 2019)

Cette masse supplémentaire est incluse pour prendre en compte la masse de tous les éléments n'ayant pas été évalués dans les estimations détaillées.

(2.21)

Avec : le coefficient de pénalité global pris entre 0 et 1%.

Masse à vide opérationnelle de l'avion

La masse à vide de l'avion en opération est constituée de la masse structurelle, de l'équipage

et des éléments opérationnels.

_WOE

_Wfuel

(2.22)

2.2.2.5. Masse maximale au décollage

W payload

La masse de l'avion au décollage est donnée par la relation suivante :

(2.23)

Avec :

la masse à vide opérationnelle (inclus la masse structurelle, l'équipage et les éléments

opérationnels).

la masse d'emport de carburant.

la charge utile de l'avion.

L'équation (2.23) peut être réécrite sous la forme de rapports de poids comme suit :

34

(2.24)

Par ailleurs, la fraction de masse entre l'atterrissage et le décollage est donnée par la relation suivante (Raymer, 2006) :

W TO

=

_{W W}

OE + payload

₁ - ₁ + ( ₁ -

? _{W W f f}

_LA TO )( ₁ )

+ + ?

? _ess trap ?

_{WLA i} + ₁

=? W

_{W W}

_{TO i} = _{0 i}

(2.25)

L'équation (2.25) peut être réécrite comme il suit :

(2.26)

La combinaison des équations (2.24) et (2.26) donne :

(2.27)

Le rapport entre les poids à l'atterrissage et au décollage s'obtient par la relation suivante :

_n

(2.28)

Dans cette relation, les indices 0 et n correspondent respectivement au début de la phase de

décollage et à la fin de la phase d'atterrissage. Le rapport de poids entre chaque phase
est donné par le tableau 2.2 précédemment présenté. En particulier, le rapport des poids en croisière et pendant l'attente sont donnés par les équations de Breguet et d'endurance. L'expression de l'équation de Breguet pour la distance maximale parcourue à vitesse de croisière est donnée comme suit (Raymer, 2006) :

_V ? _L ? ? _W ?

_{cr i}

_R = ? ? ? ?

_{TSFC D}

? ? ? ?

_{cr i} + ₁

_R

l11 W Où : [nm] est la distance parcourue.

(2.29)

35

[kt] est la vitesse de l'avion en croisière.

[lb/hr/lb] est le taux de consommation spécifique des moteurs.

est la finesse de l'avion en croisière.

Pour un jet, la finesse en croisière représente 86,6% de la finesse maximale (Raymer, 2006).

( )max

L _D ? ?

ln W i

= ? ?
TSFC ? ?

W _i + ₁

_Wfuel WTO ~ _WOE ~ W payload

(2.30)

Ainsi, le rapport des poids pendant la croisière peut être déduit comme suit :

_W ? _ . ?

_{E TSFC}

_i + _{1 max}

_exp ?

W _l ? ( )

_{L D}

_i ? ?

_max

(2.31)

L'endurance pour un avion de type jet est donnée par la relation ci-après (Raymer, 2006) :

= _l

Emax W LA = W ZF + W réserve

(2.32)

L'équation (2.31) permet de déduire le rapport des poids pendant la phase d'endurance.

(2.33)

Masse maximale de carburant

La connaissance de la masse maximale au décollage de l'avion permet de déduire la capacité maximale d'emport de carburant.

(2.34)

Masse maximale de l'avion à l'atterrissage

Avec l'hypothèse que l'avion atterrit avec un niveau de carburant correspondant à la réserve, le poids à l'atterrissage est donné par la relation suivante :

W ZF = _WOE + Wpayload

(2.35)

Où :

est le poids de l'avion à sec, c'est-à-dire sans carburant.

La trainée d'onde étant négligeable (l'avion vole en dessous de Mach 0,8), le coefficient de trainée CD s'exprime comme suit :

36

est le poids de la réserve de carburant.

Pour un avion de ligne, Torenbeek estime que le poids maximal admissible pour atterrir est 10% supérieur au poids maximal de l'avion à sec (Torenbeek, 2013).

(2.36)

Où :

est le poids maximal de l'avion à zéro carburant.

2.3. Dimensionnement du groupe de propulsion

Cette section traite de l'évaluation des performances et des caractéristiques du groupe de propulsion requis au regard des contraintes de la mission à satisfaire. Spécifiquement, il s'agira tout d'abord de déterminer la poussée maximale que devront développer les moteurs, pour assurer la propulsion de l'aéronef. Par la suite, la poussée unitaire ainsi que les dimensions du moteur seront déterminées.

2.3.1. Poussée maximale des moteurs

La poussée maximale que devrait délivrer les moteurs pour propulser l'avion sera considérer dans ce travail comme étant la poussée disponible desdits moteurs au niveau de la mer. Pour la déterminer, la démarche ici consiste à estimer tout d'abord la poussée requise et la poussée disponible en croisière et, par la suite déduire la poussée maximale au niveau de la mer.

2.3.1.1. Poussée requise en croisière

₁

₂

En vol subsonique de croisière et sans trainée d'onde, la poussée requise est la poussée minimale nécessaire à l'aéronef pour vaincre la trainée ; ce qui se traduit par l'équation ci-après :

T _{R =D=} ? _V SC D

₂

(2.37)

37

(2.38)

Où est le coefficient global de trainée du BWB au complet (moteurs et empennage

inclus).

La combinaison des équations (2.37) et (2.38) permet d'obtenir l'expression de la poussée requise en croisière, en fonction l'altitude de vol (à travers la densité) et de la vitesse de l'avion.

(2.39)

2.3.1.2. Poussée disponible en croisière

_{1 2 kS W}

2 cr

Par définition, la poussée disponible à l'altitude de croisière est la poussée maximale que doivent délivrer les moteurs lorsque l'avion vole à vitesse maximum (Anderson, 1999). En d'autres termes, la poussée disponible en croisière correspond à la poussée requise à vitesse maximale. Analytiquement, cela se traduit par :

( "

? _T = _{P V SC}

_{dispo max 0,}

_{H D} bwb _{V S}

? ?

P max ?

H cr

(2.40)

₂

₂

₂

(2.41)

_V = _1,0525 ? V cr

_max

est la vitesse maximale atteignable par l'avion en croisière.

Par analogie avec les avions régionaux TAW de taille comparable (cf. annexe 1) tels que le BAe 146, le CRJ 1000 ou encore le ARJ21-900, la vitesse maximale de l'avion pourrait être définie entre 5% et 5,5% supérieure à la vitesse de croisière. Ainsi, pour le BWB la vitesse maximale en croisière sera définie comme suit :

La poussée disponible délivrée par les moteurs à cette altitude devrait être supérieure à la poussée requise pour vaincre la traînée.

(2.42)

38

2.3.1.3. Poussée maximale au niveau de la mer

Le modèle de poussée de Mattingly (1987) présenté ci-après est un des plus répandu et il a servi de référence à de nombreux travaux sur les moteurs (Roux, 2005 ; Ghazi, et al. 2015). Il permet de déterminer pour un moteur de type turbosoufflante à haut taux de dilution, la poussée générée en fonction de l'altitude et du nombre de Mach de vol. Torenbeek caractérise les turbosoufflantes à haut taux de dilution comme ayant un taux de dilution compris entre 4 et 10 (Torenbeek, 2013). Par ailleurs dans ses travaux, Bardela a montré que le modèle de Mattingly est fiable à plus de 98%, pour la prédiction de la poussée du Cessna Citation X (Bardela, 2017).

(2.43)

Où :

est la disponible pour une altitude et un nombre de Mach donné.

est la poussée des moteurs au niveau de la mer.

est le rapport entre la masse volumique de l'air à l'altitude H et la masse volumique de l'air au niveau de la mer.

est le nombre de Mach de vol.

T SL

_{T H M}

( )

_{0,568 0,25 1,2}

( )3

? M

Du modèle de poussée de Mattingly (E-2.43), la poussée totale maximale au niveau de la mer se déduit aisément.

_dISPO

_a0,6 ? +

_1,1 - _{0,045 BPR}

	, W = 0,084 T e eng eng			(2.44)

(2.45)

2.3.2. Poids et dimensions des moteurs

L'estimation de la poussée maximale au niveau de la mer permet par la suite de déterminer le poids et les dimensions du moteur. Raymer (2006) propose les relations suivantes pour se faire.

39

(2.46)

(2.47)

Où :

[lb] est le poids d'un moteur en livre.

[in] est la longueur d'un moteur en pouce. [in] est le diamètre d'un moteur en pouce. [lb] est la poussée d'un moteur au décollage.

est le nombre de Mach maximal. est le taux de dilution.

_V = _V

_{min (})max
L D ? _{S C}
thrust _{D 0,
W k} 2.3.3. Altitude de vol au maximum de distance

Lorsque l'avion vole à finesse maximale, la poussée est minimale. Cette vitesse qui minimise

la poussée est donnée par la relation suivante (Raymer, 2006) :

(2.48)

Par ailleurs, la vitesse qui maximise la distance parcourue pour un avion à réaction est donnée par la relation suivante (Raymer, 2006) :

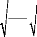
(2.49)

Sachant que la densité de l'air varie avec l'altitude, il est possible de construire la courbe d'évolution de la vitesse de croisière au maximum de distance, en fonction de l'altitude de vol. Les équations (2.50) et (2.51) donnent respectivement l'expression de la densité de l'air dans la troposphère (entre 0 et 11 km) et la stratosphère (entre 11 et 20 km).

40

(2.50)

(2.51)

Où :

[kg/m³] est la densité de l'air au niveau de la mer.

[K/m] est le taux de variation de la température en fonction de l'altitude

[m] est l'altitude de vol.

[K] est la température de l'air au niveau de la mer.

[m/s²] est la constante gravitationnelle sur terre. [J/kg/K] est la constante des gaz parfaits.

[kg/m³] est la densité de l'air à la tropopause. [K] est la température de l'air à la tropopause. [m] est l'altitude à la tropopause.

2.4. Design de la surface verticale et du train d'atterrissage

Cette rubrique présente la méthodologie utilisée pour le dimensionnement de la surface verticale du BWB, ainsi que de son train d'atterrissage.

2.4.1. Design de l'empennage vertical

Les avions de type BWB ne possèdent pas d'empennage conventionnel tel que pour les avions classiques de configuration TAW. En effet, les BWB n'ont pas besoin d'empennage horizontal; par conséquent, leur empennage se réduit aux surfaces verticales. L'empennage vertical est la composante permettant de contrôler les mouvements latéraux de l'aéronef.

41

2.4.1.1. Procédure de design de l'empennage vertical

Les paramètres qui doivent être déterminés au cours du processus de design de la surface

verticale sont les suivants (Sadraey, 2012) :

- Surface de l'empennage (Sv) ;

- Longueur de bras de levier (lv) ;

- Type de profil de la section ;

- Allongement (AR_v) ;

- Effilement (ë_v) ;

- Corde à l'extrémité (Ctv) ;

- Corde à la racine (Crv) ;

- Corde moyenne aérodynamique (MAC) ;

- Envergure (b_v) ;

- Angle de flèche .

Par ailleurs, l'étude de Larkin (2017) sur la stabilité des BWB recommande une inclinaison de

la surface verticale d'un angle par rapport à la direction verticale, afin d'améliorer la

stabilité de l'appareil.

La figure ci-dessous illustre la procédure de design suivie pour le dimensionnement de l'empennage vertical.

42

^{Déterminer l'allongement, l'effilement et}

^{l'angle de flèche}

^{Identifier et prioriser les requis du design}

^{Sélectionner le coefficient d'empennage (Cv)}

^{Déterminer l'angle de dièdre si}

^{Déterminer l'envergure, la corde à la racine, à}

^{l'extrémité et moyenne}

^{Choisir la position de l'empennage et}

^{déterminer la longueur du bras de levier (lv)}

^{Choisir la configuration de l'empennage}

^{Déterminer l'air totale de l'empennage}

^{Choisir le type de profil de la section}

^non

^{Requis de design}

^satisfaits ?

^nécessaire

^{Vérifier la stabilité}

^{(statique et dynamique)}

^{de l'avion}

^{Fin du design}

Figure 2.3 : Procédure de design la surface verticale (adapté de Sadraey, 2012)

^oui

43

2.4.1.2. Détermination des paramètres de l'empennage vertical

La figure ci-après présente les paramètres types d'un empennage vertical classique.

_S = _C

_{V V}

_{b S}

_{w w}

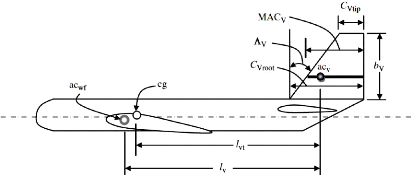
Figure 2.4 : Paramètres d'empennage vertical (Sadraey, 2012)

_CV = _0,0242

L'aire de la surface verticale s'obtient à l'aide de la relation suivante (Sadraey, 2012 ; Raymer, 2006) :

_lV (2.52)

Avec :

la surface totale de l'empennage vertical.

l'envergure de l'aile principale.

la surface alaire (surface projetée de l'aile) ;

la longueur du bras de levier (longueur entre le quart de corde l'aile principale et le quart de corde l'empennage vertical).

Larkin (2017) dans ses travaux montre que pour un BWB, la surface verticale est optimale

pour un coefficient de volume et un angle d'inclinaison (Larkin et al,

2017). L'empennage vertical étant une demi-aile, son envergure s'obtient par la relation :

(2.57)

44

(2.53)

Avec :

l'envergure de l'empennage vertical.

l'allongement de l'empennage vertical, compris entre 1,3 et 2,0 dans la catégorie d'avion

générale (Raymer, 2006).

? + + ?

_{2 1} A _V A V

_C = ?

_C ?

_{V rV}

3 ? + ?

₁ A V

La corde moyenne aérodynamique se déduit par la relation suivante :

(2.54)

La corde à la racine se déduit de l'équation suivante :

₂

(2.55)

Avec :

la corde à la racine de l'empennage vertical.

l'effilement de l'empennage vertical, compris entre 0,3 et 0,6 dans la catégorie d'avion générale (Raymer, 2006).

Connaissant l'effilement et la corde à la racine, la corde à l'extrémité est déduite par l'équation suivante :

(2.56)

En assumant que l'empennage vertical est de forme droite trapézoïdale, l'angle de flèche au

bord d'attaque est donné par la relation suivante :

? -

? = ?

arctan rV

_C C tV

_LE , _V

b _v ?

45

2.4.2. Design du train d'atterrissage

Le train d'atterrissage assure la liaison entre l'avion et le sol ; c'est la composante grâce à laquelle les mouvements de l'avion au sol sont possibles. Ces mouvements comprennent les manoeuvres telles que : le taxi dans la zone aéroportuaire, le roulage dans les phases de décollage et d'atterrissage, l'amortissement de l'impact d'atterrissage, le freinage, etc.

2.4.2.1. Configuration du train d'atterrissage

La plupart des avions commerciaux et de combat utilisent un train d'atterrissage rétractable (dans le fuselage et/ou dans l'aile) de type tricycle (Corke, 2003). Contrairement aux trains d'atterrissage fixes, les trains rétractables présentent l'avantage de diminuer la trainée aérodynamique pendant le vol lorsqu'ils sont escamotés à l'intérieur de l'aéronef.

_lng

Dans le cadre de ce travail, le choix du type de train d'atterrissage pour le BWB se fera en s'inspirant des avions historiques à tube et aile (TAW) de taille comparable.

Par ailleurs, le train d'atterrissage doit être convenablement disposé autour du centre de gravité de l'avion, afin que celui-ci soit en équilibre au sol. La figure 2.5 illustre un avion au sol vu de profil. Howe (2000) recommande que les localisations par rapport au centre de gravité des trains avant et arrière soient contraintes par la relation géométrique suivante :

(2.58)

Où :

lmg

est la distance entre le train avant et le centre de gravité de l'avion. est la distance entre le train arrière et le centre de gravité de l'avion.

Figure 2.6 : Positionnement transversal et vertical du train d'atterrissage par rapport au centre de gravité (Howe, 2000)

46

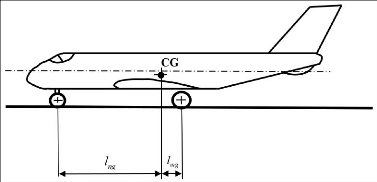
Figure 2.5 : Positionnement longitudinal du train d'atterrissage par rapport au centre de
gravité (Howe, 2000)

Howe (2000) propose de même, dans le plan en élévation, les limites de disposition des trains avant et arrières par rapport à la ligne centrale au sol de l'avion d'une part, et par rapport à la position verticale du centre de gravité d'autre part. Le positionnement du train d'atterrissage de l'avion dans le plan en élévation est donné par la figure 2.6.

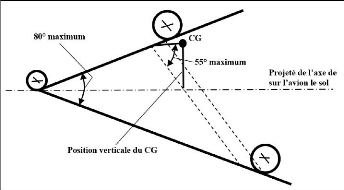
47

2.4.2.2. Dimensionnement des roues du train d'atterrissage

La taille de roue du train d'atterrissage est proportionnelle au poids de l'avion. Spécifiquement, la taille de la roue principale est estimée en assumant que celle-ci supporte 90% du poids total de l'avion (Corke, 2003). Cette estimation est faite en utilisant des formules empiriques basées sur les approximations statistiques de données historiques.

Le diamètre et la largeur de la roue principale se calculent à l'aide de la relation suivant (Corke, 2003) :

ou (2.59)

Avec :

Où :

[in] est le diamètre de la roue principale.

[in] est la largueur de la roue principale.

[lb] est le poids supporté par une roue principale.

[lb] est le poids total de l'avion.

est le nombre total de roues principales.

Les coefficients A et B dépendent du paramètre calculé (diamètre ou largeur) d'une part, et de la catégorie d'avion d'autre part. Pour un avion de ligne, le calcul du diamètre de la roue

s'effectue avec : et . La largeur de la roue qu'en à elle se calcule avec

et (Corke, 2003, p.100). Une fois la taille de la roue du train

d'atterrissage principal déterminée, la taille de la roue avant (roue de nez) est déduite. Raymer (2006) préconise que la taille de la roue de nez soit définie au moins à 60% et au plus à 100% de la taille de la roue principale.

48

2.5. Estimation du coefficient de trainée à portance nulle du BWB

Dans ses travaux, Velazquez (2020) évalue le coefficient de trainée à portance nulle du BWB en ne considérant que le corps aérodynamique de l'avion (fuselage et aile extérieure). Les trainées de friction dues au groupe moteur (nacelle et pylon) et à l'empennage vertical n'ont pas été prises en compte. Il est donc nécessaire d'estimer le coefficient de trainée généré par ces éléments, afin d'obtenir le coefficient global de trainée à portance nulle de l'avion complet.

_neng

2.5.1. Inventaire des sources de trainée n VT

En opération, chaque composant externe de l'avion est une source de trainée. Pour un avion complet, le coefficient de trainée se détermine par sommation des coefficients de trainée de chaque composant pris individuellement (Corke, 2003 ; Raymer 2006). Dans le cas du BWB, la trainée est essentiellement générée par le fuselage, l'aile extérieure, le groupe de propulsion et l'empennage vertical. Ainsi, le coefficient global de trainée à portance nulle du BWB peut être estimé à l'aide de la relation suivante :

_CD0 , _pylon

C _D0 , _VT

(2.60)

Où :

est le coefficient de trainée à portance nulle du fuselage et de l'aile extérieure évalué

par Velazquez à l'aide de la simulation numérique.

est le coefficient de trainée à portance nulle de la nacelle d'un moteur.

est le coefficient de trainée à portance nulle du pylon d'un moteur. est le coefficient de trainée à portance nulle d'une surface verticale. est le nombre de moteur.

est le nombre de surfaces verticales.

49

2.5.2. Estimation du coefficient de trainée parasite d'un élément

Corke (2003) et Raymer (2006) donnent l'expression générale de la trainée parasite d'un composant (j) externe (faisant obstacle au flux d'air) de l'avion comme suit :

(2.61)

Où :

est me coefficient de friction de la plaque plane assimilée au composant.

est le facteur de forme du composant.

est le facteur d'interférence du composant.

est la surface mouillée du composant.

est la surface de référence de l'avion (surface alaire).

Détermination du coefficient de friction :

Le coefficient de friction utilisé pour déterminer vient des études sur les plaques planes. Il

dépend du nombre de Reynolds, du nombre de Mach et de la rugosité (Corke, 2003 ; Raymer

2006).

_Re =

Pour un écoulement laminaire, le coefficient de friction a pour expression :

(2.62)

Avec est le nombre de Reynolds défini comme suit :

_r

?

(2.63)

Où :

[m/s] est la vitesse du flux d'air par rapport au composant. [m²/s] est la viscosité cinématique de l'air.

50

[m] est une longueur de référence qui dépend du composant. Pour une aile Corke (2003) et

Raymer (2006) suggèrent de prendre : . Pour tout autre composant, sera pris
comme étant la longueur du composant dans le sens de l'écoulement.

Pour un écoulement turbulent, le coefficient de friction a pour expression :

(2.64)

Où est le nombre de Mach de vol.

Corke (2003) suggère par ailleurs que l'écoulement soit considéré comme turbulent lorsque :

Détermination du facteur de forme :

Le facteur de forme est introduit afin d'estimer l'augmentation du coefficient de friction au-dessus de la trainée de viscosité, dû à la séparation de l'écoulement (Corke, 2003).

Pour l'aile, l'empennage et le pylon, le facteur de forme s'exprime comme suit (Corke, 2003 ; Raymer 2006) :

4 0? FF wing =[1+,6 C ? + 100 (t J · [1,35Mâ,18 (cos ?m )0,28 ( )m m m Où : (x c)m est la position sur la corde, du point d'épaisseur maximale. (t O. est l'épaisseur relative maximale du profil. ?mest l'angle de flèche à épaisseur maximale.

(2.65)

Où : est la longueur totale de la nacelle.

51

Pour la nacelle, le facteur de forme se détermine à l'aide de la relation suivante (Raymer 2006) :

_S ? _2,003 ? _S ( _{t c )m} ? _5%

Où :

(2.66)

est le diamètre maximal de la nacelle.

est la longueur de la génératrice du cône du diffuseur d'entrée d'air.

? S ref ? _1,977 + _{0,52 t c} ?

( )

( _{t c )m} ? _5%

Détermination du facteur d'interférence :

La trainée parasite croit avec l'interférence mutuelle entre les composants (Raymer, 2006).

Pour la nacelle montée directement sur l'aile, l'interférence est . Si la nacelle est

montée sous l'aile à une distance avoisinant son diamètre (Raymer, 2006).

Pour un empennage en V, l'interférence est d'environ 3%, soit : . Pour un

empennage en H, l'interférence est d'environ 8%, soit : . Pour les empennages

conventionnels, l'interférence est prise de 4 à 5% (Raymer, 2006).

_{wet airfoil ref}

_airfoil ? _m ?

Détermination de la surface mouillée :

La surface mouillée est la surface totale du composant en contact avec le flux d'air.

? _{?D L} + _{X D}

( _nacelle nacelle 0,5 nacelle

² )

Pour les composants de type aile tels que l'empennage et le pylon, une approximation de la surface mouillée est donnée par Corke (2003).

si (2.67)

Swet

si (2.68)

Pour la nacelle, la surface mouillée sera estimée comme étant la surface d'enveloppe totale.

L nacelle

_Swet

_nacelle

(2.69)

52

2.6. Estimation des performances de l'avion

Cette section présente la méthodologie utilisée pour l'estimation des paramètres de performances du BWB, à l'instar des distances de décollage et d'atterrissage, des performances en montée et en descente, du facteur de charge et du domaine de vol.

2.6.1. Estimation des distances de décollage et d'atterrissage

Les distances de décollage et d'atterrissage d'un aéronef dépendent de plusieurs paramètres de performances intrinsèques à l'appareil à l'instar du coefficient de portance maximal, de la charge alaire et du ratio poussée sur poids. Ainsi, à partir des paramètres aérodynamiques et de poussée de l'avion, une estimation des distances de décollage et d'atterrissage peut être faite.

2.6.1.1. Estimation de la distance de décollage (Corke, 2003)

Pendant la phase de décollage, l'avion accélère d'une vitesse nulle à une vitesse de décollage VTO, puis décolle de la piste pour atteindre une altitude minimalement supérieure à la hauteur d'obstacle de référence Hobstacle. La distance pour accomplir ce décollage est STO.

Pour un avion commercial, la vitesse et la hauteur d'obstacle minimale de décollage sont données par la "Federal Aviation Regulations" (FAR) tel qu'il suit (FAR Part 25) :

et [ft] (2.70)

De façon détaillée, le décollage se subdivise en quatre phases distinctes à savoir :

- Le roulage au sol ;

- La rotation ;

- La transition ;

- La montée.

La figure ci-après présente une illustration de chacune de ces phases de décollage.

53

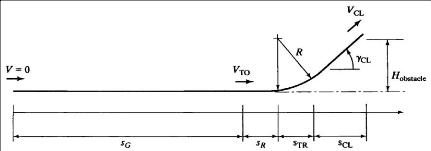
Figure 2.7 : Schéma d'illustration des phases de décollage (Corke, 2003)

La distance totale de décollage est la somme des distances de chacune des quatre phases.

(2.71)

? ? ? ?

_{T T}

? ?=? ?

? ? ? ?

_W W max

· Distance de roulage au sol (Corke, 2003)

La distance de roulage ( ) est déterminée en assumant que le ratio poussée-poids est

maximal à .

dV _{2 2}

_{VTO 1} ? _{f V} ?

_{2 TO}

= = ? + ?

? _{2 ln 1}
0 _f + _{f V 2 gf}

_{1 2 2} ? f ₁ ?

C'est-à-dire : à

Et se calcul à l'aide de l'expression ci-après :

? ?

f 1 = ? - ?

SG

? ? W

(2.72)

Où et sont des coefficients adimensionnels qui se calculent comme suit :

_T

?

(2.73)

54

Et,

(2.74)

Avec :

le coefficient de friction en roulement de la piste au décollage (asphalte sèche).

[slug/cu.ft] la masse volumique de l'air à l'altitude de décollage.

[lb/ft²] la charge alaire de l'aéronef.

est le coefficient de portance lorsque l'avion roule.

est le coefficient de trainée à portance nulle de l'avion.

Coefficient de trainée supplémentaire causée par les volets (slotted flaps).

Le coefficient de trainée supplémentaire lorsque les trains sont sortis peut être estimé par la relation empirique ci-après :

Où :

_A = _{A b 2 H}

_{effectif w w w}

H w

(2.75)

est la surface frontale projetée des trains d'atterrissage.

k effectif

=

? _{A e}

_{effectif effectif}

est une fonction de corrélation qui dépend du poids de l'avion au décollage. _{A b} Le coefficient d'efficacité d'envergure (keffectif) est donné par la relation :

_{w w}

(2.76)

Où :

est l'allongement effectif pour le décollage et l'atterrissage.

[ft] est la hauteur entre l'aile et le sol.

et sont respectivement l'allongement et l'envergure de l'aile.

55

est le coefficient d'Oswald effectif (Obert, 2009).

V ²

_{g n}

( )

- ₁

· Distance de rotation (Corke, 2003)

Pendant la phase de rotation au décollage, l'angle d'attaque augmente jusqu'à

. Par convention, la durée de la rotation pour un avion de ligne est de 3 secondes. Pendant cette

manoeuvre, la vitesse de l'avion est de et la distance parcourue au sol est :

=

(2.77)

· Distance de transition (Raymer, 2006)

Le rayon de courbure durant la transition est donné par la relation ci-après :

RTR		TR		(2.78)

Où :

est la vitesse de transition ;

est le facteur de charge durant la transition ; [ft/sec²] est l'intensité de la pesanteur.

La distance parcourue pendant la transition est donnée par l'équation ci-après :

(2.79)

_?climb

Où : est l'angle de montée au décollage.

· Distance pendant la montée (Corke, 2003)

La phase de montée commence à la fin de la transition et se termine une fois que l'avion a atteint l'altitude prescrite Hobstacle. Durant cette montée, la distance parcourue est donnée par la relation ci-après :

56

(2.80)

Où :

[ft] est la hauteur d'obstacle pour un avion civil ;

[ft] est la hauteur atteinte durant la transition.

2.6.1.2. Estimation de la distance d'atterrissage (Corke, 2003)

De même que le décollage, l'atterrissage se déroule en quatre phases distinctes à savoir :

- L'approche ;

- La transition ;

- La phase de roue libre ;

- Le freinage.

La figure ci-après présente une illustration de chacune de ces phases d'atterrissage.

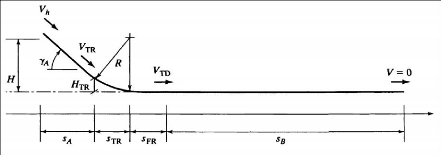
Figure 2.8 : Schéma d'illustration des phases d'atterrissage (Corke, 2003)

· Distance pendant la descente

La descente se fait à vitesse constante avec moteur éteint (poussée est nulle) de la hauteur d'obstacle de 50 pieds jusqu'à la hauteur de transition HTR. Pour les avions de transport, la valeur absolue de l'angle de descente n'est pas supérieure à 3°.

57

(2.81)

· Distance pendant la transition

Durant la transition, l'avion vole le long d'un arc de cercle avec un rayon de RTR. Pour un avion commercial, la vitesse pendant la transition est :

(2.82)

La distance parcourue pendant la transition est donnée par la relation ci-après :

(2.83)

· Distance de roue libre (Corke, 2003)

Pendant la phase de roue libre à l'atterrissage, l'avion maintient une vitesse constante de VTD. Par convention, la durée de la rotation en roue libre pour un avion de ligne est de 3 secondes., la distance parcourue au sol pendant cette manoeuvre est :

[ft] (2.84)

Où :

[ft/s] est la vitesse lorsque l'avion touche le sol.

· Distance de freinage (Corke, 2003)

La distance de freinage pendant l'atterrissage s'obtient par la même démarche que la distance

de roulage ( ) au décollage. Durant cette phase, le pilote applique les freins jusqu'à l'arrêt

de l'avion et la distance parcourue se calcul à l'aide l'expression ci-après :

_{2 2}

- _{1 dV}

_{0 1} ? _{f V}

_{2 TD}

_S = = ? +

? _{2 ln 1}

^B _{g f f V}

_{2 TD}

V + _{2 gf}

_{1 2 2} ? f 1

(2.85)

Où et sont des coefficients adimensionnels qui se calculent comme suit :

_W

(2.89)

58

(2.86)

Et,

(2.87)

Si les moteurs sont équipés d'inverseurs de poussée , alors la poussée inverse est telle que :

est le coefficient de friction en roulement de la piste à l'atterrissage.

La distance totale d'atterrissage est la somme de chacune des distances des quatre phases. En plus de cela, la FAR-25 recommande de majorer la distance totale d'atterrissage d'un facteur de 1,667, pour prendre en compte les différences entre les pilotes (Raymer, 2006).

(2.88)

2.6.2. Performance en montée et en descente

Pendant la montée ou pendant la descente, les paramètres les plus importants sont : le taux de montée (respectivement de descente), la vitesse et l'angle de montée (respectivement de descente).

2.6.2.1. Performance en montée

Pour un aéronef, le taux de montée n'est autre que la composante verticale de la vitesse ascensionnelle de l'appareil. Ainsi, pour un angle de montée ?climb, le taux de montée est déterminé comme suit (Raymer, 2006) :

? - ?

_{T D}

_RC = _{V sin} ? _V

climb = ? ?

? ?

59

Sachant que :

et

L'expression du taux de montée devient :

=

_{W S T}

_{3 P C} ? _W ? ?

_{D 0,} bwb ? ?

(2.90)

La vitesse à laquelle le taux de montée est maximal est donnée par la relation suivante (Raymer, 2006) :

2 1

r ?

₁ + ? ? + _{12 C k} ?

_{D 0, bwb}

_W ?

Vmax climb RD = V sin Y = sin Y				T W 2cosYdes des des des S PCL		(2.91)

2.6.2.2. Performance en descente

Pour un aéronef, le taux de descente est la composante verticale de la vitesse de descente de l'appareil. Pour un angle de descente ?des, le taux de descente à poussée nulle est déterminé comme suit (Corke, 2003) :

_{D CD}

_{sin I} = _{COs I} = _{COs I}

_{des des des}

_{L CL}

(2.92)

La combinaison des équations (2.92) et (2.93) permet d'obtenir une expression plus générale du taux de descente.

Par ailleurs ,

(2.93)

60

			(2.94)

La vitesse à laquelle le taux de descente est minimal s'obtient à l'aide de l'équation suivante : (Raymer, 2006) :

n max = _3,8

		(2.95)

2.6.3. Facteur de charge et domaine de vol de l'avion

Les conditions de vol d'un aéronef sont définies par une multitude de paramètres intrinsèques et extrinsèques à l'instar de la vitesse, la position du centre de gravité, l'attitude, la direction et l'intensité du vent, etc. Pour un vol économique et sécuritaire, la variation de ces paramètres dans une limite règlementaire conditionne le domaine de vol de l'avion.

Le diagramme V-n constitue une synthèse graphique du domaine de vol d'un aéronef. Concrètement, il s'agit d'une enveloppe dans laquelle l'avion peut voler en toute sécurité, et dans le respect des exigences réglementaires RAC/FAR.

n min

WTO 10000

Facteur de charge limite réglementaire :

Pour les avions type commerciaux, le Règlement de l'Aviation Canadien (RAC, 2019) stipule

que le facteur de charge de manoeuvre limite positif n doit être compris entre une valeur

minimale nmin et une valeur maximale nmax, avec :

_2,1 +

+

₂₄₀₀₀ (2.96)

_WTO

Et,

[lb] est le poids maximal de l'avion au décollage.

Le facteur de charge de manoeuvre limite négatif ne doit pas être inférieur à 0,4 fois le facteur de charge positif, pour les catégories d'avion de ligne.

61

Variation du facteur de charge avec la vitesse :

À une altitude constante, le facteur de charge peut être exprimé en fonction de la vitesse de vol par la relation suivante :

(2.97)

À basse vitesse, le facteur de charge est limité par le coefficient de portance maximal. Ainsi, pour les basses vitesses, la relation (2.97) précédente devrait être remplacée par l'équation ci-après :

(2.98)

est le facteur de charge maximal atteignable, lorsque En définitive, le facteur de charge à considérer est :

(2.99)

2.7. Équilibre et stabilité de l'avion

Cette section présente l'approche théorique nécessaire à l'analyse de la stabilité et de l'équilibre d'un aéronef. Ainsi, les notions de stabilité, de marge statique et d'équilibre de l'avion seront présentées.

2.7.1. Notions de stabilité d'un avion

Pour un avion, la stabilité renvoie à la capacité qu'à ce dernier à revenir à l'état de vol stable initial après avoir subi une perturbation. La stabilité d'un avion est une propriété d'extrême importance pour sa validation en conception. En réalité, aucun avion n'est rigoureusement stable ; ils doivent cependant posséder un niveau de stabilité acceptable, pour garantir un pilotage ergonomique d'une part, et le confort des passagers d'autre part. plus un avion est

(2.100)

62

stable, plus il est facile à piloter. A contrario, un avion trop stable sera difficile à manoeuvrer. Ainsi, les gros avions de ligne sont conçus pour être très stables, ce qui n'est pas le cas avec les avions de chasse ou d'entraînement où une plus grande manoeuvrabilité est nécessaire. Avec les avions conventionnels à tube et aile, l'empennage horizontal joue un rôle primordial pour assurer la stabilité de l'appareil. En dépit de leurs forts potentiels aérodynamiques, les BWB présentent des problèmes de stabilité assez compliqués dus au faible bras de moment et aux mauvaises caractéristiques d'assiette (Okonkwo, 2016). Ceci s'explique en grande partie du fait de l'absence d'empennage horizontal.

Il existe deux formes de stabilité que sont la stabilité statique et la stabilité dynamique. La stabilité statique d'un avion est communément interprétée pour décrire sa tendance à converger vers l'état d'équilibre initial suite à une petite perturbation de l'assiette (trim). La stabilité dynamique quant à elle décrit le mouvement transitoire impliqué dans le processus de rétablissement de l'équilibre suite à la perturbation (Cook, 2012). Ainsi, la stabilité statique renvoie aux actions de contrôle requises, afin d'établir les caractéristiques nécessaires pour garantir l'équilibre de l'avion. Bien entendu, la stabilité dynamique est également importante, en ce sens qu'elle détermine en grande partie les caractéristiques des mouvements transitoires de l'avion, suite à une perturbation autour de sa position de vol stabilisé.

Ce projet se limitera à l'évaluation de la stabilité statique longitudinale du BWB en déterminant les marges statiques et les caractéristiques d'assiette.

2.7.2. Marge statique et conditions de stabilité

La marge statique est un concept utilisé pour caractériser le degré de stabilité statique et de contrôlabilité d'un avion. La marge statique est définie comme étant la distance entre le centre de gravité de l'avion et son point neutre. Le moment de tangage d'un avion sans empennage, dans un vol équilibré quasi stable de masse constante en atmosphère normale et sans effets de compressibilité pour de petits angles d'attaque est donné par l'équation suivante (Okonkwo, 2016) :

? - ?

_{X X}

_{cg np}

_C = _C + ?

_C

_M , _{cg M 0, cg L} ?

? c ?

63

L'équation (2.101) donne l'expression du coefficient des moments d'un BWB, par rapport au

centre de gravité. La dérivée de cette expression par rapport à l'angle d'attaque permet

En posant et , l'équation (2.100) devient :

SCM , _cg

_M a Sa

(2.101)

Où :

est le coefficient de moment par rapport au centre de gravité.

est le coefficient de moment à portance nulle par rapport au centre de gravité.

et sont respectivement les distances du centre de gravité et du point neutre, par

rapport au nez de l'avion.

est la corde moyenne aérodynamique de l'avion.

C _M ?

_K = - = - -

( )

_{h h}

_{n cg np}

La dérivée de l'équation (2.101) par rapport à donne l'équation (2.102).

(2.102)

_C=

Avec : et

La marge statique est définie par la relation suivante :

_CL? (2.103)

est généralement donnée en pourcentage. Pour que l'avion soit stable, la marge statique

doit être positive ; c'est-à-dire que le centre de gravité devrait se situer devant le point neutre. Si le centre de gravité se trouve derrière le point neutre, l'avion est jugé longitudinalement instable. Pour un avion de transport, la marge statique positive avec le centre de gravité maximum arrière doit être comprise entre 5 et 10 % (Raymer, 2006).

2.7.3. Coefficient de moment et équilibre de l'avion

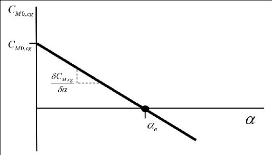
64

d'obtenir un coefficient connu sous l'appellation de « coefficient de stabilité longitudinal », tel que présenté ci-après :

(2.104)

Où :

est le coefficient de stabilité longitudinale.

Au regard des équations (2.101) et (2.104), et sachant que le coefficient de portance de l'avion varie linéairement en fonction de l'angle d'attaque, il apparait clairement que les coefficients de moment et de stabilité longitudinale eux aussi varient linéairement en fonction de l'angle d'attaque. L'équation (2.105) ci-dessous donne l'expression de cette droite.

(2.105)

La figure 2.9 présente la variation du coefficient de moment avec l'angle d'attaque.

Figure 2.9 : Variation du coefficient de moment avec l'angle d'attaque (cas stable)

Sur cette figure représente l'angle d'attaque absolue à l'équilibre de l'avion, pour une

condition de vol donnée. À cet angle, les forces et les moments agissant sur l'avion se trouvent dans un état d'équilibre.

_M0

(2.108)

65

Par ailleurs, les conditions nécessaires pour la stabilité d'un avion peuvent être résumées à la satisfaction des équations suivantes (Cook, 2012) :

et (2.106)

Explicitement, cela revient à dire que :

- Le coefficient de moment à portance nulle doit être positif ;

- Le coefficient de stabilité longitudinale doit être négatif ;

- L'angle d'attaque à l'équilibre doit être compris dans la plage des angles de vol de

l'avion.

Cependant, pour pouvoir obtenir l'équation explicite de la droite de coefficient de moment exprimée par les équations (2.102) et (2.105) précédents il faudrait au préalable, déterminer le coefficient de moment à portance nulle de l'avion et, par la suite trouver une expression de son coefficient de portance en fonction de l'angle d'attaque.

À l'équilibre, la somme des moments de tangage au centre de gravité de l'avion est nulle. L'équation d'équilibre des moments s'écrira alors comme suit :

(2.107)

Où :

est le moment de tangage de l'avion à portance nulle.

est la force de portance générée par le corps central de l'avion.

est la force de portance générée par l'aile extérieure de l'avion.

=

( )

L ow

L'équation (2.107) peut être réécrite, pour obtenir l'équation (2.108), puis l'équation (2.109) :

_{M L}

( ) _M

_{cg fus cg}

( ) ? _{V S c}

² ( ) ? _{V S c}

_{2 2}

_{1 2 1 2} ( _{1 2} ) ? _{V S c}

_{ref ref ref}

66

₂

?

?

(2.112)

(2.109)

À partir de l'équation (2.109), la déduction de l'expression du coefficient de moment à portance nulle est directe.

(2.110)

Où :

et sont respectivement les coefficients de moment à portance nulle du corps

central et de l'aile extérieure.

et sont respectivement les cordes aérodynamiques moyennes du corps central et de
l'aile extérieure.

et sont respectivement les surfaces plan du corps central et de l'aile extérieure.

I

cos ² _{AR A} ?
( )
_C ?
_basse . vitesse ? +
_{AR 2cos} A ?

En général, le coefficient de moment à portance nulle est connu pour les profils d'aile. Pour une aile complète (c'est-à-dire en trois dimensions) d'allongement et d'angle de flèche connus, le coefficient de moment à portance nulle peut être déterminé à partir de la relation d'ajustement donnée par l'équation (2.111) pour de basses vitesses subsoniques (Raymer, 2006).

_C = ?

_{m 0,3D m 0,2D}

_LE

_LE

(2.111) Pour des vitesses subsoniques élevées (proche de Mach 0,8) les effets du transsonique entrent en jeu et augmentent le moment de tangage. Dans ce cas, le coefficient de moment à portance nulle augmenterait d'environ 30% (Raymer, 2006). L'équation (2.111) ci-dessus deviendrait alors :

_{AR cos A} ?

? LE

( )

_C = ? ?

_{1,3 C}

_m 0,3D ? _{m 0,2D}

_Mach 0.8 ? +

_AR 2cos ALE

67

Pour ce qui est de la droite de portance de l'avion, l'on peut remarquer que les forces de portance agissant sur la BWB au complet proviennent du corps central et de l'aile extérieure. Elles peuvent donc être exprimées comme suit :

_{S S}

_{fuS ow}

_C = _C + _C

_L , _{bwb L ,fuS L} , _ow

_{S S}

_{ref ref}

(2.113)

Pour une condition de vol donnée, l'expression générale de la force de portance est donnée par l'équation suivante :

(2.114)

Ainsi, la combinaison des équations (2.113) et (2.114) permet d'obtenir l'expression du

coefficient de portance du BWB, en fonction des coefficients de portances du fuselage ( )

et de l'aile extérieure ( ), eux même fonction de l'angle d'incidence.

(2.115)

Les coefficients et seront explicitement exprimés dans la section suivante, en

fonction de l'angle d'attaque ; ce qui permettra par la suite de déduire une expression du coefficient de portance du BWB en fonction de .

L'objectif de ce chapitre était dans un premier temps de présenter la méthodologie utilisée pour estimer la masse du BWB ainsi que la poussée des moteurs et le dimensionnement des surfaces verticales. Par la suite, la démarche d'évaluation des performances de l'avion à basse vitesse et en croisière a été présentée. Dans le chapitre qui suit, les résultats de l'estimation de la masse de l'avion, des caractéristiques des moteurs, du design des surfaces verticales ainsi que des performances de l'appareil seront présentés et discutés.

68

CHAPITRE 3

RÉSULTATS ET DISCUSSIONS

Ce chapitre présente respectivement les résultats de calcul de la masse détaillée de l'appareil, du dimensionnement du groupe de propulsion, du dimensionnement de la surface verticale et du train d'atterrissage. Par la suite, les résultats de l'évaluation des performances de l'appareil à l'instar des distances de décollage et d'atterrissage, des taux de montée et de descente, sont également présentés.

3.1. Résultats de l'évaluation de la masse du BWB

L'évaluation détaillée de la masse du BWB a été réalisée suivant l'algorithme présenté à la section 2.2. L'estimation de la masse de l'aile extérieure a été effectuée à partir des relations empiriques de Howe (2000), Kundu (2019) et Torenbeek (2013) respectivement, afin d'apprécier la valeur de la masse prédite, selon le modèle d'aile considéré.

Le tableau 3.1 ci-après est une synthèse détaillée de la prédiction de la masse du BWB, pour chaque groupe de composants.

70

Tableau 3.1 : Prédiction de masse détaillée du BWB

GROUPE	DÉTAIL DES ÉLÉMENTS	MASSE [kg] (modèle d'aile de Howe)	MASSE [kg] (modèle d'aile de Kundu)		MASSE [kg] (modèle d'aile de Torenbeek)	ÉLÉMENTS STRUCTURAUX
Structure de la Cellule
	2630	2754	3468
	604	606	614
	3337	3339	3355
	1205	1207	1213
	1620	1628	1674
	5850	5859	5910
	767	767	767
	560	560	560
	85	85	85
	291	291	291
	97	97	97
	136	136	136
	15	15	15
	11	11	11
	2918	2933	3015
	20128	20288	21212		CHARGE UTILE PAYANTE
Passagers, y compris les bagages à main	8165	8165	8165
	2688	2688	2688
	1200	1200	1200
	12053	12053	12053		ÉLÉMENTS OPÉRATIONNELS
Équipage	425	425	425
	208	209	215
	633	634	640		CARBURANT
Carburant dans l'aile (50%) Carburant dans le fuselage (50%)	8 876	8 920	9 171		MASSE MAXIMALE AU DÉCOLLAGE (MTOW)
41 690		41 895	43 076

71

Au regard des résultats présentés dans le tableau 3.1, il apparait que les masses totales prédites avec les modèles d'aile de Howe (2000) et de Kundu (2019) sont très proches. L'erreur relative absolue entre les deux est un peu moins que 0,5%, donc quasi nulle. Par ailleurs l'erreur relative absolue entre les prédictions de Howe (2000) et de Torenbeek (2013) est d'environ 3,4%, donc moins de 5%, ce qui semble raisonnable.

Cependant, les modèles d'aile de Howe (2000) et de Kundu (2019) aboutissant à une même prédiction de masse d'une part, et étant donné que le modèle de Kundu est le plus récent d'autre part, la masse finale du BWB sera considérée comme étant celle prédite par Kundu (2019), d'autant plus que ce modèle est celui qui prend en compte le plus grand nombre de paramètres, pour l'estimation de la masse de l'aile.

Le tableau 3.2 présente la répartition de la masse de l'avion. Cette structure de décomposition de la masse est très rependue dans le domaine aéronautique ; elle servira donc de base pour la comparaison du BWB à d'autres avions.

Tableau 3.2 : Répartition de la masse du BWB

Paramètre	Notation	Valeur		Unité	Charge utile payante
CU	12 053	kg		Masse maximale de carburant
MFW	8 920	kg		Masse à vide sortie usine
MEW	20 288	kg		Masse à vide en opération
OEW	20 923	kg		Masse maximale à l'atterrissage
MLW	36 273	kg		Masse maximale sans carburant
MZFW	32 975	kg		Masse maximale au décollage
MTOW	41 895	kg		Facteur de structure-usine
fsempty	0,484	-		Facteur de structure opérationnel
fsoew	0,499	-

Ainsi, le facteur de structure opérationnel (fsoew) du BWB serait de 0,50 soit 10% plus petit que le facteur de structure moyen des avions conventionnels TAW de taille comparable (cf. annexe 1). Cette différence montre à suffisance que par rapport aux avions conventionnels, le BWB a une capacité d'emport plus grande.

72

Par ailleurs, en comparaison avec les BWB présentés à la section 1.1, le facteur de structure à vide de l'avion (fsempty) est 18,3% supérieur à celui du bombardier furtif B-2A Spirit, et 15,4% inférieur à celui du Northrop YB-35.

3.2. Coefficient de trainée à portance nulle du BWB

Comme mentionné dans la section 2.5 précédente, le coefficient de trainée à portance nulle du BWB au complet s'obtient par sommation des coefficients de trainée du fuselage, de l'aile extérieure, du groupe de propulsion (nacelle et pylon) et des surfaces verticales. Par ailleurs, du fait de l'interdépendance entre le coefficient de trainée parasite de l'avion (à travers les coefficients de trainée de la nacelle et du pylon) et les caractéristiques du groupe de propulsion, une boucle de calcule entre ces deux entités a été nécessaire pour obtenir des résultats.

Le tableau 3.3 présente les résultats de calcul du coefficient de trainée à portance nulle de l'ensemble fuselage-aile extérieure, du groupe de propulsion (nacelle et pylon), des surfaces verticales, puis du BWB en entier.

73

Tableau 3.3 : Synthèse des résultats de calcul du coefficient de trainée
à portance nulle

_3,192 ?

_2,407 ?

10- ⁵

C _{D 0} , _bwb

Paramètre	Notation		Valeur [-]				Référence	Nombre de Reynolds
					E-2.63		Coefficient de friction
	2 ?	(			E-2.64		Facteur de forme
	2 ?	(			E-2.66 E-2.65		Facteur d'interférence
					Section 2.5.2		Surface mouillée [m^2]
					E-2.69 E-2.68		Coefficient de trainée à portance nulle
					Velazquez (2020) E-2.61
					E-2.60

₄

_10-

)

)

Ainsi, avec l'ajout des moteurs et des surfaces verticales, le coefficient de trainée à portance nulle du BWB serait de 0,0132, soit 11,4% plus élevé que l'estimation faite par Velazquez (2020).

74

3.3. Performance de la propulsion

La détermination de la poussée maximale des moteurs est intrinsèquement liée aux conditions de croisière, à l'instar de la vitesse et de l'altitude de croisière. Ces deux paramètres ont une incidence directe sur la traînée que devra vaincre les moteurs pour faire avancer l'avion.

3.3.1. Altitude de croisière pour une distance maximale

L'équation (2.49) donne l'expression de la vitesse de croisière qui maximise la distance parcourue par l'avion, en fonction de la densité de l'air (et donc de l'altitude). En assumant que l'altitude de croisière de l'avion se situerait dans la stratosphère, entre 11 et 15 km notamment, la figure ci-après présente la courbe d'évolution de la vitesse optimale de croisière en fonction de l'altitude.

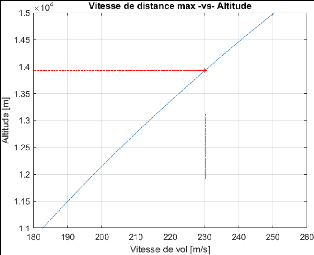
Figure 3.1 : Altitude requise en croisière en fonction de la vitesse

Ainsi, pour la vitesse de croisière de 230 m/s (755 ft/s) définie dans les requis de conception, l'avion devrait voler à une altitude de 13 890 mètres afin de maximiser la distance parcourue. L'altitude de croisière du BWB sera donc fixée à 13 900 mètres.

75

3.3.2. Poussée requise et poussée disponible en croisière

Les équations (2.39) et (2.41) donnent respectivement les expressions de la poussée requise et de la poussée disponible en croisière, en fonction de la vitesse. Ainsi, avec une vitesse maximale de 242 m/s en croisière (calculée à partir de l'équation (2.42), la poussée disponible de l'avion à l'altitude de croisière (13,9 km) serait de 8125 lbf (35,75 kN).

La figure 3.2 présente la variation de la poussée requise du BWB en croisière, en fonction de la vitesse de vol. Sur cette figure, la ligne horizontale orangée représente la poussée disponible, c'est-à-dire la poussée dont disposent les moteurs à cette altitude jusqu'à Vmax.

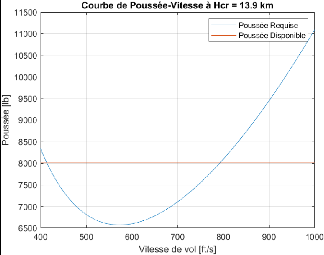
Figure 3.2 : Courbe Poussée-Vitesse du BWB

Le tableau ci-après présente les vitesses caractéristiques du domaine de vol en croisière du BWB, déduites à partir de la figure 3.2.

Tableau 3.4 : Vitesses caractéristiques du BWB en croisière

					416 ft/s
573 ft/s	755 ft/s	795 ft/s		127 m/s
175 m/s	230 m/s	242 m/s

76

est la vitesse minimale de l'avion en croisière, est la vitesse de l'avion au minimum

de poussée, est la vitesse optimale de croisière et est la vitesse maximale de l'avion.

3.3.3. Performance et dimension des moteurs

Assumons que la propulsion de l'aéronef est assurée par deux moteurs de type turbosoufflante avec un taux de dilution proche de 5 :1.

Connaissant l'altitude de vol, le nombre de Mach et la poussée disponible en croisière, la relation (2.44) de Mattingly (1987) permet de déterminer la poussée maximale des moteurs au niveau de la mer.

Le tableau 3.5 présente les caractéristiques générales de performance des moteurs du BWB notamment, la poussée disponible en croisière, la poussée maximale totale et la consommation spécifique.

Tableau 3.5 : Performances des moteurs du BWB (turbosoufflante) ? ?

? ?

Désignation	Notation	Valeur en Impérial			Valeur en SI		Poussée requise à vitesse de croisière Poussée disponible en croisière Poussée maximale totale Poussée maximale unitaire x2 Consommation spécifique Rapport "poussée sur poids" en croisière Rapport "poussée sur poids" au décollage
W cr ? ? T ? ? ? ? W to ? ?	7803 8125 37717 18859 0,60 0,085 0,397	lb lb lb lb lb/lb - h		34,34 35,75 167,77 82,98	kN kN kN kN

_T

La poussée totale nécessaire pour la propulsion du BWB serait donc de 168 kN au niveau de la mer. En comparaison avec les avions de taille assimilée tels que le CRJ1000 de Bombardier (129 kN), le Sukhoi Superjet 100 (154 kN) ou encore le Antonov An-158 (134 kN), cette valeur de poussée semble élevée, bien que raisonnable. En effet, le ratio poussée-poids de 0,397 du

77

BWB au décollage est supérieur à tous ceux des avions TAW de taille comparable présentés en annexe 1, de même qu'à ceux des BWB présentés à la section 1.1, en occurrence le B-2A, les X-48B et X-48C. Sachant que les limites de vitesses et altitude de vol du BWB sont assez proches de ceux des avions TAW comparables, cette valeur assez élevée du ratio poussée-poids de l'avion pourrait traduire une trainée plus importante avec du BWB qu'avec les avions conventionnels de taille comparable.

Connaissant la poussée maximale développée par un moteur, les relations (2.45) à (2.47) permettent de déterminer respectivement la masse du moteur, sa longueur et son diamètre. Ces dimensions permettront d'estimer l'encombrement à l'arrière de la cellule centrale, où seront placés les moteurs et les surfaces verticales, tel le cas des BWB X-48B et X-48C.

Le tableau 3.6 présente le poids et les dimensions longueur et diamètre estimés du moteur.

Tableau 3.6 : Poids et dimensions d'un moteur

Paramètre	Notation	Valeur en SI			Valeur en Impérial		Masse du moteur à sec
	1 495	kg		3 297	lb	Longueur du moteur
	2,812	m		9,224	ft	Diamètre du moteur
	1,715	m		5,626	ft

3.4. Caractéristiques et positionnement des surfaces verticales

La surface verticale n'étant pas censée générer de la portance en vol rectiligne (suivant l'axe longitudinal de l'avion) le profil d'aile symétrique NACA 0012 sera utilisé, car comme il ne produit aucune portance à incidence nulle, l'empennage ne créera pas de mouvements de lacet en vol rectiligne. Le tableau 3.7 présente les paramètres d'entrées pour le design de la surface verticale.

78

Tableau 3.7 : Données du design

Paramètre	Notation	Valeur		Unité	Coefficient VT
	0,0242	-		Envergure de l'aile principale
	34,4	m		Surface alaire
	173,9	m^2		Longueur du bras de levier VT
	9,0	m		Allongement VT
	1,8	-		Effilement VT
	0,5	-

Le tableau 3.8 présente une synthèse des résultats du design de l'empennage vertical. Compte tenu de la valeur relativement élevée de la surface totale d'empennage, la solution a été d'opter pour un double empennage vertical, comme sur les BWB X-48B et X-48C de Boeing, le A0.30 des Allemands, ou encore le MEVERIC de Airbus.

Tableau 3.8 : Résultats du design de la surface verticale

Paramètre	Notation	Valeur en SI			Valeur en Impérial		Surface totale VT
	16,080	m^2		173,03	ft^2	Nombre de surfaces verticales
	2	-		2	-	Envergure VT
	2,689	m		8,82	ft	Corde à la racine VT
	3,845	m		12,61	ft	Corde à l'extrémité VT
	1,921	m		6,30	ft	Corde moyenne aérodynamique VT
	2,989	m		9,804	ft	Angle de flèche au bord d'attaque
	35,5	deg		35,5	deg

79

À partir des caractéristiques géométriques des moteurs et des surfaces verticales ci-dessus présentées, les figures 3.3 et 3.4 illustrent la configuration du BWB avec ses moteurs placés à l'arrière du fuselage, tel que c'est le cas pour les BWB expérimentaux X-B48 et X-C48 de Boeing ou encore le MEVERIC de Airbus. Le dessin de l'avion a été réalisé à l'aile du logiciel CATIA V5 en partant de la géométrie initiale réalisée par Velazquez (2020). L'annexe 3 présente les positions des points ainsi que les profils d'ailes nécessaires à la modélisation 3D du fuselage et de l'aile de l'avion.

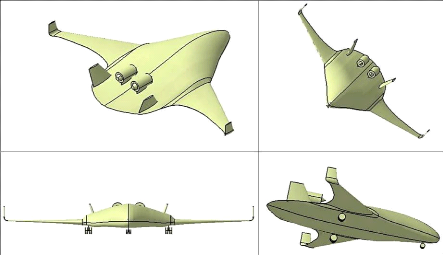
Figure 3.3 : Vue multiple du BWB, moteurs en arrière du fuselage

80

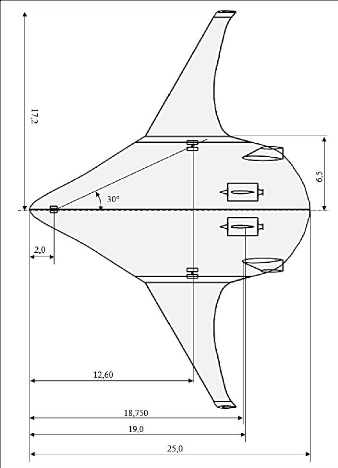
Figure 3.4 : Vue de dessus du BWB, moteurs et surfaces verticales placés

3.5. Type et dimensions du train d'atterrissage

La configuration du train d'atterrissage retenue pour le BWB est de type tricycle rétractable, comme pour le CRJ1000. Le train principal (à l'arrière) sera constitué de quatre roues tandis que le train avant possèdera deux. Le tableau 3.9 présente les dimensions (largeur et diamètre en pouce), des roues constituant le train d'atterrissage.

81

Tableau 3.9 : Dimensions des roues du train d'atterrissage

Type de roue	Nombre	Diamètre (in)		Largeur (in)	Roues du train principal
4	37,35	12,33		Roues de nez
2	24,28	8,02

3.6. Performances au décollage et à l'atterrissage

Les aéroports les plus hauts du monde sont à une altitude d'environ 4000 mètres. Ainsi, Il serait judicieux d'estimer les distances de décollage et d'atterrissage du BWB au niveau de la mer d'une part, et à 4500 mètres d'altitude d'autre part. Le tableau 3.10 présente les données nécessaires à l'évaluation des distances de décollage et d'atterrissage de l'avion.

Tableau 3.10 : Données de calcul des distances de décollage et d'atterrissage

Désignation		Notation	Valeur		Unité	Longueur de piste
BFL		2 000	m		Altitude maximale de l'aéroport
-		4 500	m		Masse maximale au décollage
MTOW		41 895	kg		Masse maximale à l'atterrissage
MLW		36 273	kg		Coefficient de friction au roulage
Décollage (aucun freinage)		0,05	-
		0,50	-		Inversion de poussée à l'atterrissage (40% de la poussée maximale) SL
		- 67,20	kN

Le tableau 3.11 présente les performances de décollage et d'atterrissage du BWB au niveau de la mer d'une part, et à un aéroport situé à 4500 mètres d'altitude d'autre part.

82

Tableau 3.11 : Distances de décollage et d'atterrissage du BWB

Décollage					Atterrissage
0					0			Altitude à l'aéroport [m]
			4500	Altitude à l'aéroport [m]			4500
(SL)					(SL)			Angle de montée [deg]
4°			4°	Angle d'approche [deg]	-2°		-3°	Roulage au sol [m]
		628,6	864,2	Approche [m]		388,2	176,7	Rotation [m]
		171,6	171.6	Transition [m]		96,6	228,5	Transition [m]
		133,8	133,8	Roue libre [m]		202,4	254,1	Montée [m]
		85,8	85,8	Freinage [m]		347,4	612,3	Distance totale de
				Distance totale				décollage [m]
		1 020	1 256	d'atterrissage [m]		1 725	2 120

Au regard des valeurs de distances de décollage et d'atterrissage présentées dans le tableau 3.11 ci-haut, il en ressort que le BWB serait capable de décoller dans n'importe quel aéroport sur une distance de moins de 1260 mètres, bien en dessous de la limite maximale de 2000 mètres imposée dans les requis du design. Par ailleurs, sa configuration actuelle ne lui permettrait pas de se poser sécuritairement dans les aéroports à haute altitude avec une longueur de piste de 2000 mètres, car il lui en faudra 120 mètres de plus. Cependant, comme les aéroports situés à des altitudes élevées disposent de pistes plus longues le BWB pourra être opérationnel dans ces aéroports.

Pour finir, en comparaison avec les avions de taille assimilée tels que le CRJ1000 de Bombardier avec une distance de décollage de 2120 mètres, ou encore le Antonov An-158 avec une distance de décollage de 1900 mètres, il s'avère que le BWB présente un excellent avantage de performances au décollage.

Pour ce qui est de l'atterrissage, la distance minimale de piste pour que le BWB puisse se poser au niveau de la mer serait de 1725 mètres. En comparaison avec le CRJ1000 de Bombardier avec une distance d'atterrissage de 1750 mètres, il en ressort que les deux avions ont des performances quasi similaires à l'atterrissage.

83

3.7. Performances en montée et en descente

Pendant la montée ou pendant la descente, les paramètres les plus importants sont : le taux de montée (respectivement de descente), la vitesse et l'angle de montée (respectivement de descente).

3.7.1. Performances pendant la montée du BWB

L'équation (2.90) donne l'expression du taux de montée en fonction de la vitesse rectiligne de l'avion et de l'angle de montée. La figure 3.5 présente la variation du taux de montée suivant la vitesse de montée et l'angle de montée.

Au regard de cette figure, il en ressort que l'angle de montée de l'avion n'a quasiment aucune influence sur le taux de montée. Par contre, le taux de montée est fortement dépendant de la vitesse de montée de l'avion. Lorsque l'avion atteint la vitesse de 485 ft/s (147,8 m/s), le taux de montée est maximal. En dessous de cette valeur, le taux de montée croît avec la vitesse de l'avion et, au-dessus, le taux de montée décroit avec la vitesse de l'avion.

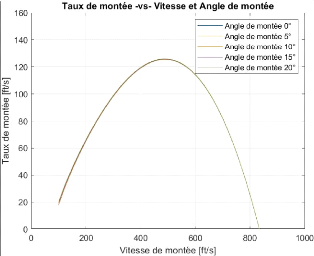
Figure 3.5 : Courbe de variation du taux de montée du BWB

84

3.7.2. Performances pendant la descente

L'équation (2.94) donne l'expression du taux de descente à poussée nulle du BWB, en fonction de la vitesse rectiligne et de l'angle de descente. La figure 3.6 présente la variation du taux de descente suivant la vitesse de descente et l'angle de descente.

Au regard de cette figure, il en ressort que l'angle de descente du BWB a peu d'influence sur son taux de descente. Par contre, ce taux de descente est fortement dépendant de la vitesse de descente de l'avion. Pour une vitesse de descente de 400 ft/s (122 m/s), le taux de descente est minimal. En dessous de cette valeur, le taux de descente décroît avec la vitesse de l'avion et, au-dessus, le taux de descente croît avec la vitesse de l'avion.

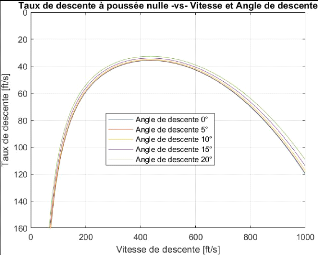
Figure 3.6 : Courbe de variation du taux de descente du BWB (moteurs éteints)

n min,sup = + _2,33

3.8. Facteur de charge et domaine de vol du BWB

Le poids maximal de l'avion étant de 92362 lb, d'après les recommandations du RAC, le

facteur de charge minimal positif de l'avion devrait être de et son maximum ne

devrait pas dépasser 3,8. Ainsi, le facteur de charge limite supérieur du BWB sera pris à

85

. Pour le facteur de charge minimal négatif, la règlementation recommande qu'il

soit fixé à 40% de la limite supérieure, soit : . Ainsi, le facteur de charge limite
inférieure du BWB sera pris à .

Les équations (2.97) et (2.98) donnent l'expression du facteur de charge de l'avion en fonction de la vitesse de vol. A partir de ces équations, le diagramme V-n du BWB a été construit tel qu'illustré à la figure 3.7.

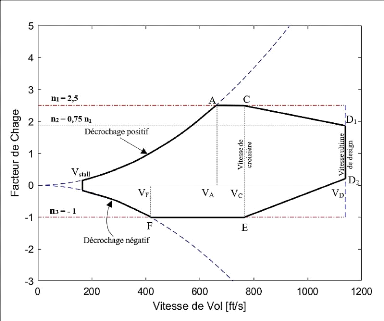
Diagramme V-n à Hcr = 13,9 km

Figure 3.7 : Diagramme V-n du BWB, à altitude de croisière

Sur ce diagramme, les courbes OA et OF correspondent à l'état de décrochage de l'avion et sont obtenues à partir de la relation aérodynamique donnée par l'équation (2.98).

Pour des vitesses inférieures à VA (incidence positive de l'aile) et VF (incidence négative), les charges maximales pouvant être appliquées à l'avion sont régies par CLmax. AC et FE représentent les facteurs de charge opérationnels maximaux pour l'avion. Lorsque la vitesse de l'avion est supérieure à la vitesse de croisière de calcul VC, les lignes de coupure CD1 et

86

D2E soulagent les cas de calcul à couvrir, car il n'est pas attendu que les charges limites soient appliquées à la vitesse maximale (Megson, 2016).

La limite D1D2 est atteinte à la vitesse de vol la plus élevée, qui est la vitesse de « plongée ». VD = 1,5 Vcruise est donc la vitesse ultime de design à ne jamais dépasser (Corke,2003).

3.9. Synthèse des spécifications générales du BWB

Maintenant que les principales caractéristiques géométriques et de performances de l'avion ont été déterminées, le tableau 3.12 ci-après présente une synthèse des spécifications finales de l'appareil. Comme présenté dans le ce tableau, le moteur sélectionné pour la propulsion de l'avion est le GE Passport 20-19BB1A. Il s'agit d'un moteur de type turbosoufflante qui fait partir de la famille des moteurs à réaction commerciaux « Passport » du constructeur General Electric. Réputé pour sa fiable et son économie en carburant, ce moteur équipe la nouvelle famille d'avions d'affaires Global 7500 de Bombardier. Par ailleurs, le moteur BR715-A1-30 de Rolls-Royce qui équipe actuellement le jet régional Boeing 717-200 (poussée maximale au niveau de la mer : 18710 lbf / 84,2 kN) pourrait également être utilisé pour propulser le BWB.

Tableau 3.12 : Synthèse des caractéristiques générales du BWB

Caractéristiques commerciales			Motorisation		Catégorie Équipage Équipage Cabine Passagers max
Avion de ligne régional 2 3 100		Type Références Poussée unitaire (SL, ISA) Nombre de moteurs Poussée totale	Turbosoufflante GE Passport 20- 19BB1A 18920 lbf (84,16 kN) 2 37840 lbf (168,32 kN)	Caractéristiques géométriques
25 m 34,4 m 5,4 m 316 m^2		Performances
			Mach 0,78 (828 km/h) Mach 0,82 (871 km/h) 0,397

87

Masse et capacité d'emport			Performances
			2 500 km 45 min 13 900 m 1020 m 1 725 m 38,4 m/s ou 2304 m/min 10,0 m/s ou 602 m/min	OEW MEW Charge utile payante MTOW Carburant Facteur de structure à OEW
20 923 kg 20 288 kg 12 053 kg 41 895 kg 8 920 kg 0,50

Parvenu au terme de ce chapitre dont l'objectif était de présenter et discuter les résultats de l'estimation de la masse du BWB et d'évaluer ses performances, il en ressort que l'avion aura une masse totale au décollage d'environ 41895 kg, donc 20,2% de moins que la masse prédite par Delacroix (2017) et 6,3% de moins que celle prédite par Velazquez (2020). Par ailleurs, le facteur de structure opérationnel de l'avion estimé à 0,50 signifie que le BWB aura une capacité d'emport relative plus importante que celle des avions de taille comparable à l'instar du CRJ1000 de bombardier (fsOEW = 0,557), du ARJ21-900 (fsOEW = 0,567), ou encore de l'Antonov An-148 (fsOEW = 0,503). Placés à l'arrière du fuselage avec les surfaces verticales, les moteurs du BWB généreront une poussée maximale de 168 kN. Le chapitre qui suit sera réservé au centrage des masses du BWB ainsi qu'à l'analyse de sa stabilité statique, afin de se rassurer que dans la configuration actuelle, l'avion est statiquement stable d'une part, et que le niveau de stabilité est acceptable d'autre part.

88

CHAPITRE 4

CENTRAGE ET STABILITÉ DU BWB

Pendant les phases de conception, de fabrication et d'opération d'un avion, le centrage des masses fait l'objet d'une attention particulière, afin de garantir la stabilité de l'appareil. Ce chapitre présente en première section le centrage des masses du BWB et la détermination de son centre de gravité. La seconde section quant à elle est réservée à la détermination du point neutre de l'avion d'une part, et à l'analyse de sa stabilité statique d'autre part.

4.1. Centrage des masses du BWB

La position du centre de gravité est une considération déterminante pour assurer la stabilité de l'avion, pendant toute l'enveloppe de vol. Après avoir obtenu les masses des composants (c'est-à-dire la masse détaillée) présentées à la section 3.1, il devient possible de localiser le centre de gravité de l'avion.

4.1.1. Méthodologie de détermination du centre de masse de l'avion

Statistiquement, l'estimation de la position du centre de gravité de l'avion au complet équivaut à déterminer le barycentre de l'ensemble des centres de gravité des groupes de composants constituant l'appareil, pondéré de leur masse respective. Le centre de gravité de chacun de ces groupes de composants est défini sur la base des données historiques disponibles et du retour d'expérience de l'équipe de design.

Analytiquement, le centre de gravité dans la direction longitudinale d'un avion se détermine comme suit :

_{n n}

_{X m X m}

cg = ? ?

_{i i i}

_i = _{1 i=1}

_Xcg

X i

_mi

(4.1)

Où :

est la position du centre de gravité de l'avion par rapport au nez.

est la position du centre de gravité du groupe de composant i considéré. est la masse du groupe de composant i considéré.

90

Cependant, en opération, la masse de carburant et la charge utile d'un avion sont des quantités variables. Ceci a pour conséquence de modifier la position de centre de gravité en tout temps. Ainsi, chaque combinaison de carburant et de charge utile donne une position du centre de gravité. Pour cette raison, le calcul du centre de gravité de l'avion se fait suivant trois considérations à savoir : à masse maximale au décollage (MTOW), à masse à vide opérationnelle (OEW) et à masse maximale sans carburant (MZFW). Ainsi, l'équation (4.2) donne la position du centre de gravité par rapport au nez de l'avion avec MTOW.

_{r r}

_{mzfw mzfw mzfw}

= ? ? m mzfw

_{X m X}

_{cg i i i}

_i = _{1 i} = ₁

(4.2)

De même, la position du centre de gravité par rapport au nez de l'avion avec OEW est donnée par l'équation (4.3).

(4.3)

Et, la position du centre de gravité par rapport au nez de l'avion avec MZFW est donnée par l'équation (4.4).

(4.4)

Les résultats obtenus des équations (4.2) à (4.4) ci-dessus donnent la plage de localisation du centre de gravité de l'avion. Dans cette plage, la valeur minimale représentera le centre de gravité maximum avant tandis que la valeur maximale représentera le centre de gravité maximum arrière.

4.1.2. Détermination du centre de gravité du BWB

Comme dit plus haut, le centre de gravité du BWB est le barycentre des centres de gravité de toutes les composantes de l'avion. Pour les éléments en forme d'aile tels que l'aile extérieure, le fuselage et les surfaces verticales, Raymer (2006) suggère que leur centre de gravité se situerait à 40% de la corde moyenne tandis que Kundu (2019) l'estime à 30%. Ainsi, en considérant la moyenne des prescriptions de Raymer et de Kundu, les centre de gravité des corps en aile dans ce travail sera pris à 35% de leurs cordes moyennes respectives.

91

Par ailleurs Raymer (2006) et Kundu (2019) préconisent tous deux de prendre le centre de gravité du moteur à 50% de sa longueur. Les éléments de la charge utile doivent être repartis autour du centre de gravité de l'avion. Pour ce qui est des éléments du sous-groupe « équipements et instruments », ceux-ci seront positionnés de telle manière que leurs centres de gravité se retrouvent entre 30 et 50% de la longueur totale de l'avion.

Le tableau 4.1 présente la localisation longitudinale des centres de gravité des éléments constituant l'avion.

92

Tableau 4.1 : Localisation du centre de gravité du BWB (moteurs à l'arrière du fuselage)

GROUPE	DÉTAIL DES ÉLÉMENTS	MASSE [kg]	CG Xi [m]		Position du CG	ÉLÉMENTS
Structure de la Cellule	STRUCTURAUX
Aile	2754	14,8	35%
Empennage VT	606	20,7	35%
Fuselage (cellule centrale)	4546	10,9	35%
Train d'atterrissage AV	244	2,0	5-10%
Train d'atterrissage AR	1384	12,6	Donnée par Howe (2000)
Groupe de Propulsion	5859	19,0
Équipement & Instruments
Air Conditionné	767	7,5	30-50%
Avioniques	560	2,5	10-40%
Systèmes Hydrauliques	85	10,0	40-50%
Systèmes Électriques	291	7,5	30-50%
Dégivreur	97	7,5	30-50%
Instruments	136	7,5	30-50%
Équipements de manutention	15	7,5	30-50%
APU	11	7,5	30-50%
Ensemble Fournitures	2933	7,5	30-50%
(sièges, mobilier, etc.)					CHARGE UTILE
Passagers, y compris les bagages à main	8165	9,3	80-100%
Conteneurs LD-3 (qté 2)	2688	9,3	80-100%
Eau, nourriture, équipements de sécurité...	1200	5,0	20-40%		ÉLÉMENTS
Équipage	425	2,5	10%		OPÉRATIONNELS
Masse de pénalité	209	5,0	20-30%		CARBURANT
Carburant Aile	4480	15,0	40%
Carburant CB	4480	5,8	50-100%		MASSES DE
MTOW	41895	11,18			L'AVION
OEW	20923	12,82
MZFW	32975	11,38

De la position maximale avant (à MTOW) à la position maximale arrière (à OEW), le centre de gravité de l'avion se déplace d'environ 1,64 mètre. Nous verrons dans les sections qui

93

Au regard du tableau 4.1 précédent, il en ressort que :

· À charge maximale (MTOW), le centre de gravité du BWB est le plus en avant et se situerait à 11,18 mètres du nez de l'appareil, soit à 45% de la longueur total ;

· À masse à vide opérationnelle (OEW), le centre de gravité du BWB est le plus en arrière et se situerait à 12,82 mètres du nez de l'appareil, soit à 51,3% de la longueur totale ;

· À masse maximale sans carburant (MZFW), le centre de gravité du BWB se situerait à 11,38 mètres du nez de l'appareil, soit à 45,5% de la longueur total.

La position de chacun de ces centres de gravité sur l'avion est illustrée dans la section suivante. 4.1.3. Positionnement du centre de gravité sur l'avion

Comme présenté dans la section précédente, la position du centre de gravité du BWB varie en fonction de la masse de l'appareil. La figure ci-après illustre la localisation longitudinale du centre de gravité de l'avion, selon la masse totale considérée.

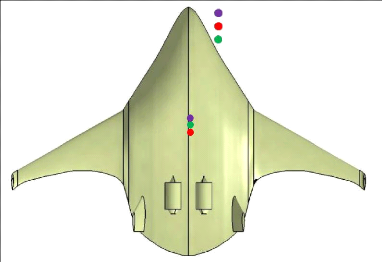
Centre de gravité à MTOW (11,18 m) Centre de gravité à OEW (12,82 m) Centre de gravité à MZFW (11,38 m)

Figure 4.1 : Positionnement du centre de gravité du BWB

94

suivent que cette variation de la position du centre de gravité de l'avion a un impact significatif sur la stabilité de l'appareil.

4.2. Point neutre et stabilité statique du BWB

Encore appelé foyer, le point neutre est le point par rapport auquel le moment des forces de portance (aile extérieure et corps central dans le cas du BWB) reste constant, quel que soit l'angle d'attaque. Pour un avion, la position du point neutre par rapport au centre de gravité influe directement sur la stabilité.

Dans toute cette section, les hypothèses suivantes seront considérées :

- L'avion vole en palier, les forces de trainée () et de poussée () sont égales ; - Les forces de trainée () et de poussée () ne créent pas de moment ;

- Les forces de portance du corps centrale ( ) et de l'aile ( ) sont verticales.

4.2.1. Détermination du point neutre du BWB

Comme dit plus haut, au point neutre, le moment des forces de portance reste constant quel que soit l'angle d'incidence de l'avion. La détermination de sa localisation est un préalable à l'étude de la stabilité statique de l'appareil.

4.2.1.1. Modélisation simplifiée de l'équilibre du BWB

La figure 4.2 présente une modélisation simplifiée du BWB, ainsi que les forces extérieures qui s'y exercent en vol en palier.

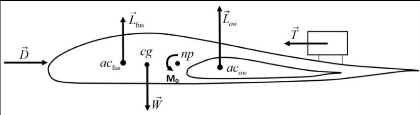
Figure 4.2 : Modèle simplifié du bilan des forces appliquées à un BWB

95

Sur cette figure, D représente le bilan des forces de trainée, T est la force de poussée totale des

moteurs, W est le poids total de l'avion appliqué au centre de gravité, est la résultante des
forces de portance générées par le fuselage (appliquée au centre aérodynamique du profil

d'aile) et est la résultante des forces de portance générées par l'aile extérieure (appliquée
au centre aérodynamique du profil d'aile également).

À l'équilibre, le bilan des forces donne :

? M _np ( L _fus ) M _np ( L _ow ) ₀

+ ? =

? ?

	(4.5)

Au point neutre, la somme des moments des forces aérodynamiques est constante, quel que soit l'angle d'attaque. Ceci se traduit analytiquement par l'équation suivante :

? ? _L X _np X ac L _ow X ac X np

? ( - ) ( )

- - ? = ₀

? fus

?? ?

(4.6)

(4.7)

Sachant que les forces aérodynamiques s'appliquant à l'avion ont pour résultante les forces de portance générées par le fuselage et l'aile extérieure, l'équation (4.7) implique :

² L OW = ? S _{OW V} C _{L OW
L} = ? _{S V} C L

_{fus fus ,fus} ,

_{2 2}

_S

_{S C S C}

_{fus L} , _ow

C _{L ,fus}

= C ow =

_Sa

_{L a L a}

_{Sa Sa}

_{1 1}

(4.8)

_fus

_ow

(4.9)

₂

Sachant que : et

Puis en posant : et

L'équation (4.9) permet de déduire la position du point neutre de l'avion :

96

(4.10)

Où :

est l'abscisse du point neutre par rapport au repère avion.

est l'abscisse du centre aérodynamique du corps central par rapport au repère avion.

est l'abscisse du centre aérodynamique de l'aile par rapport au repère avion.

est le coefficient de portance du corps central.

est le coefficient de portance de l'aile extérieure.

est la surface plan du corps central.

est la surface plan de l'aile extérieure.

Il ne reste plus qu'à déterminer chacun des paramètres de l'équation (4.10) pour trouver la position du point neutre.

4.2.1.2. Localisation des centres aérodynamiques et

La figure 4.3 présente la position des centres aérodynamiques du corps centrale et de l'aile extérieure, sur la géométrie de l'avion.

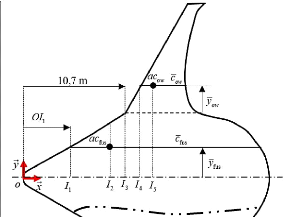
Figure 4.3 : Localisation des centres aérodynamiques du corps central et de l'aile

97

₁

(4.16)

La corde moyenne aérodynamique d'une aile trapézoïdale est donnée par la relation

suivante (Corke, 2003) :

(4.11)

Où : et sont respectivement la corde à la racine et l'effilement de l'aile.

La distance entre la corde moyenne aérodynamique de l'aile et la corde à la racine est

donnée par la relation suivante (Corke, 2003) :

(4.12)

Où : est l'envergure de l'aile.

Par simplification, le centre aérodynamique d'une aile est généralement pris au quart de sa corde aérodynamique moyenne . Au regard de la géométrie de l'avion présentée à la figure 4.3, la localisation des centres aérodynamiques du corps central et de l'aile extérieure est donnée par les relations géométriques suivantes :

X

fus =y _ac fus _tan ? LE +c
_{,fus fus}

(4.13)

(4.14)

En fonction des paramètres géométriques des ailes complètes, les équations (4.13) et (4.14) deviennent :

X ow = _OI + y ow ? _LE ow + c ow

_tan

_{ac 3} , 4

₁

₄

(4.15)

_dCL

(4.18)

98

Où :

et sont respectivement les cordes moyennes aérodynamiques du corps central et de

l'aile extérieure.

et sont respectivement les distances entre la corde à la racine et la corde moyenne

aérodynamique, du corps central et de l'aile extérieure.

et sont respectivement les angles de flèche au bord d'attache du corps central et

de l'aile extérieure.

4.2.1.3. Détermination des coefficients de portance du corps central et de l'aile

Le corps central est caractérisé par un profil aérodynamique LA2573A. Comme énoncé dans les hypothèses, nous assumerons que celui-ci s'étend symétriquement des extrémités y = 0 m à y = 6,5 m (c'est-à-dire jusqu'à la racine de l'aile extérieure). L'aile extérieure quant à elle est caractérisée par un profil aérodynamique SC(2)-0712 à ses extrémités (y = 6,5 m et y = 17,2 m). Les coordonnées des points constituant les profils du corps central et de l'aile extérieure sont présentées dans l'annexe 3.

L'équation de la droite de portance d'une aile tridimensionnelle (c'est-à-dire complète) est donnée par la relation suivante (Anderson, 1999) :

(4.17)

Où :

est l'angle d'incidence du flux d'air avec le bord d'attaque de l'aile (angle d'attaque) ; est l'angle d'attaque à portance nulle (c'est le même en 2D qu'en 3D).

La théorie de la ligne de portance de Prandtl permet d'estimer la pente de portance d'une

aile complète (Anderson, 1999). En vol subsonique compressible, la pente de portance

pour une aile en flèche s'exprime comme suit (Anderson, 1999) :

_CLa

= =

_{a A}

0 cos 0.5

da 2

₂

₁ - _M cos ² _A + ? _A

( ) ( ) ? + ( ) ( )

_0.5 ? _{a cos} ? _AR

_{0 0.5} ? _{a cos A} ? _AR

? _{0 0.5}

99

Où :

[rad^-1] est la pente de portance du profil d'aile.

est le nombre de Mach en vol subsonique.

L'angle de flèche à la moitié de la corde est donné par l'équation qui suit :

(4.19)

4.2.1.4. Résultats de calcul du point neutre et de la droite de portance du BWB

En se basant sur la démarche et les équations présentées dans les sections précédentes, le tableau 4.2 présente les données nécessaires au calcul de la localisation du point neutre de l'avion.

Tableau 4.2 : Données de paramètres géométriques de l'avion

Paramètre	Notation	Valeur	Unité
		14,5	m
Envergure
		19,9	m
		0,30	-
Effilement
		0,20	-
		240	m^2
Surface plan
		76	m^2
		25	m
Corde à la racine
		7,6	m
Angle de flèche au		57,5	deg
bord d'attaque		30	deg

100

À partir de ces données, les positions des centres aérodynamiques du corps central et de l'aile extérieure ont pu être déterminées. Le tableau 4.3 présente les différents résultats obtenus pour le calcul de ces centres aérodynamiques.

Tableau 4.3 : Localisation des centres aérodynamiques
du corps central et de l'aile extérieure

Paramètre	Notation	Valeur [m]	Équation
Corde moyenne		17,85
			E-4.11
aérodynamique		5,24
Position de la corde		2,98
moyenne par rapport à			E-4.12
la corde racine		3,87
Position des centres		14,24	E-4.15
aérodynamiques		9,14	E-4.16

Il en ressort au vu de ces valeurs que les centres aérodynamiques du corps central et de l'aile extérieure sont distants d'environ 5,1 mètres.

Par la suite, après avoir déterminé les équations des droites de portance du corps central et de l'aile extérieure, la position du point neutre du BWB peut être calculée. Le tableau 4.4 présente les différents résultats ayant permis à leurs déterminations.

101

Tableau 4.4 : Droites de portance et point neutre du BWB

Paramètre	Notation	Valeur/Expression	Unité	Référence
Angle de flèche au 1/2 de la corde moyenne		20,29 15,21	deg deg	E-4.19
Allongement		0,876 5,211	- -	(Corke, 2003)
Angle d'attaque à portance nulle		- 0,75 - 4,50	deg deg	Profil LA2573A Profil SC(2)-0712
Pente de portance du profil d'aile 2D		6,251 6,889	rad^-1 rad^-1	Profil LA2573A Profil SC(2)-0712
Pente de portance de l'aile 3D		0,03639 0,10899	deg^-1 deg^-1	E-4.18
Droite de portance (en degré)			- - -	E-4.17 E-2.115
Point neutre			m	E-4.10

Ainsi, le point neutre du BWB se situerait à environ 11,624 mètres du nez, soit à 46,5% de la longueur totale de l'avion.

Par ailleurs, la figure 4.4 présente la droite de portance du BWB en fonction de l'angle d'attaque.

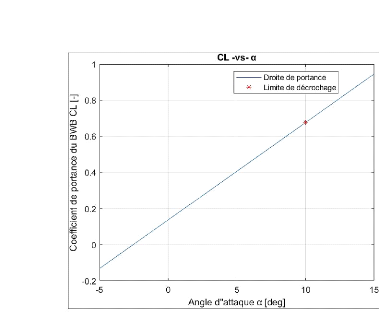
102

Figure 4.4 : Droite de portance du BWB

D'après les estimations de Velazquez (2020), la limite de décrochage de l'avion se situerait à un angle d'attaque de 10°.

Du fait que cette droite de portance a été obtenue à partir des relations analytiques de la théorie des lignes de portance de Prandtl, une validation a été effectuée par comparaison avec la droite de portance obtenue par Velazquez (2020) à l'aide de la simulation numérique.

La figure 4.5 présente à gauche, la superposition de la droite de portance du BWB obtenue analytiquement à partir de la théorie de la ligne portante de Prandtl avec celle obtenue par Velazquez avec une analyse CFD. À la droite de la même figure est présentée la courbe de l'erreur relative absolue entre les coefficients de portance obtenue de l'analyse CFD de Velazquez et ceux obtenus du modèle analytique développé dans ce travail.

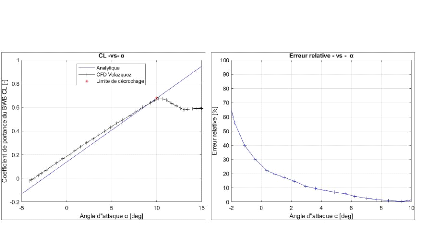
103

Figure 4.5 : Comparaison entre les droites de portance analytique et CFD du BWB

Au regard de la figure 4.5, il apparait que la droite de portance du modèle analytique développé dans ce travail est très proche de celle obtenue par Velazquez à l'aide d'une simulation CFD. Cette affirmation est confirmée par la décroissance exponentielle de l'erreur relative entre les deux approches. À partir d'un angle d'attaque de 1°, l'erreur relative est de moins de 20% et décroit jusqu'à 2% après 8,5°. À la limite de décrochage de 10°, le coefficient de portance maximale prédit par le modèle analytique est de 0,677 contre 0,673 prédit par Velazquez avec la CFD, soit une erreur relative d'environ 0,6%, ce qui semble assez faible.

À l'issue de cette analyse comparative entre le modèle analytique développé dans ce travail et l'estimation CFD faite par Velazquez, il en ressort que le modèle analytique est acceptable.

4.2.2. Analyse de la stabilité statique du BWB

Dans cette section, la stabilité statique longitudinale de l'avion sera étudiée, au regard de la marge statique d'une part et du coefficient de moment de tangage d'autre part.

4.2.2.1. Marge statique et stabilité du BWB

L'équation (2.103) donne l'expression de la marge statique de l'avion, en fonction de la position du centre de gravité et du point neutre. Pour une position de centre de gravité donnée, l'avion sera considéré longitudinalement stable si et seulement si sa marge statique est positive. Le tableau ci-après récapitule les valeurs de marges statiques obtenues, en considérant les trois positions de référence du centre de gravité de l'avion.

104

Tableau 4.5 : Marge statique du BWB (moteurs à l'arrière du fuselage)

Cm 0,2D,fus

Masse de l'avion	Centre Xcg [m]	de gravité Limite	Marge statique Kn [%]	État de stabilité
MTOW	11,18	Cg max. AV	2,59	Stable
OEW	12,82	Cg max. AR	- 7,11	Instable
MZFW	11,38	Cg nominal	1,44	Stable

Au regard des valeurs de marges statiques présentées dans le tableau ci-dessus, il apparait qu'à vide, le BWB est longitudinalement instable. En effet, le centre de gravité de l'avion à vide se trouve derrière le point neutre par conséquent, ce dernier aura tendance à cabrer du nez, rendant ainsi tout pilotage difficile, voire impossible, sans l'assistance d'un système de commande de vol automatique.

Par ailleurs, à la charge maximale au décollage comme à la charge maximale sans carburant, la marge statique de l'avion est certes positive, mais reste bien inférieure au minimum de 5% recommandé par la FAA. Par conséquent, l'avion présentera des difficultés de pilotage.

Cm 0,2D,OW

Cm 0,3D,fus

Cm 0,3D,ow

4.2.2.2. Moment de tangage et stabilité du BWB

À la section 2.7.3 précédente, le coefficient de moment du BWB a été exprimé à partir des coefficients de moment du corps central et de l'aile. Le tableau 4.6 présente les différents résultats ayant permis à la détermination du coefficient de moment de l'avion.

Tableau 4.6 : Coefficient de moment du BWB (moteurs à l'arrière du fuselage)

Paramètre	Notation	Valeur/Expression	Référence
Coefficient de moment à portance nulle du profil d'aile	C m 0 , cg	0,0177 - 0,1162	Profil LA2573A Profil SC(2)-0712
Coefficient de moment à portance nulle de l'aile 3D		0,00298 - 0,08503	E-2.112
Coefficient de moment à portance nulle du BWB		0,00873	E-2.110

105

Marge statique [%]		2,59 - 7,11 1,44	Max. AV Max. AR Nominale
Droite de portance du BWB			E-2.115
Coefficient de moment du BWB			E-2.101

Ainsi, pour les trois positions du centre de gravité de l'avion, le coefficient de moment varie linéairement avec l'angle d'attaque. La figure 4.6 présente la droite de variation du coefficient de moment du BWB en croisière, en fonction de l'angle d'attaque.

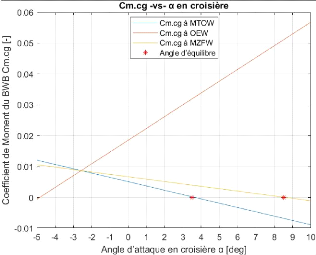
Figure 4.6 : Variation du coefficient de moment du BWB (moteurs à l'arrière du fuselage)

Au regard de la figure 4.6, les droites de variation du coefficient de moment de l'avion viennent confirmer l'analyse de stabilité effectuée précédemment à partir des valeurs de marges statiques. En effet, la pente de la droite de coefficient de moment lorsque l'avion est à vide (OEW) est positive ; ce qui signifie que dans cette situation, le BWB est instable. Par ailleurs,

Le tableau 4.7 présente les positions des centres de gravité des composants de l'avion, suite au déplacement des moteurs sous l'aile de l'appareil.

106

lorsque l'avion est à masse maximale au décollage (MTOW) ou à masse maximale sans carburant (MZFW), les pentes de leurs droites de coefficient de moment sont négatives, ce qui confirme la stabilité de l'appareil dans ces situations. Le point d'équilibre de l'avion est atteint pour les valeurs d'angle d'attaque de 3,5° et 8,5° lorsque l'avion est à MTOW et MZFW respectivement. Cependant, la valeur d'angle d'équilibre de 8,5° est assez élevée pour un avion de transport civil; par conséquent, le BWB en l'état actuel présente des défauts de stabilité et donc, il ne satisfait pas aux exigences de la réglementation en matière de transport des passagers.

Suite au défaut de stabilité de la configuration actuelle du BWB, il serait judicieux d'apporter quelques modifications au design de l'avion afin de le rendre statiquement stable. Le problème venant du fait que le centre de gravité est assez proche du point neutre, la solution la plus logique serait de déplacer vers l'arrière ou vers l'avant certains éléments structuraux, tels que l'aile ou les moteurs. En effet, déplacer l'aile vers l'arrière permettrait de reculer le centre aérodynamique de l'avion plus en arrière du centre de gravité, tandis que déplacer les moteurs vers l'avant permettrait de reculer le centre de gravité de l'appareil plus en avant du point neutre.

Cependant, changer la position de l'aile de l'avion pourrait avoir une incidence significative sur l'aérodynamisme de l'appareil tout entier, ce qui obligerait de refaire les analyses CFD. Par conséquent, la solution qui sera implémentée dans ce travail consistera à déplacer les moteurs de l'avion, pour les positionner sous l'aile de l'appareil.

4.2.2.3. Configuration de l'avion, moteurs placés sous l'aile

Déplacer les moteurs de l'arrière du fuselage pour les placer sous l'aile de l'avion permettrait d'avancer le centre de gravité de l'ensemble. Cette configuration du BWB avec les moteurs sous l'aile est similaire à celle du BWB A0.30 présenté à la section 1.1.

107

Tableau 4.7 : Localisation du centre de gravité du BWB (moteurs sous l'aile)

GROUPE	DÉTAIL DES ÉLÉMENTS	MASSE [kg]	CG Xi [m]	Position du CG
ÉLÉMENTS	Structure de la Cellule
STRUCTURAUX	Aile	2754	14,8	35%
	Empennage VT	606	20,7	35%
	Fuselage (cellule centrale)	4546	10,9	35%
	Train d'atterrissage AV	244	2,0	5-10%
	Train d'atterrissage AR	1384	12,6	Donnée par Howe (2000)
				Au voisinage
	Groupe de Propulsion	5859	11,0	du CG de
				l'avion
	Équipement & Instruments
	Air Conditionné	767	7,5	30-50%
	Avioniques	560	2,5	10-40%
	Systèmes Hydrauliques	85	10,0	40-50%
	Systèmes Électriques	291	7,5	30-50%
	Dégivreur	97	7,5	30-50%
	Instruments	136	7,5	30-50%
	Équipements de manutention	15	7,5	30-50%
	APU	11	7,5	30-50%
	Ensemble fournitures	2933	7,5	30-50%
	(sièges, mobilier, etc.)
CHARGE UTILE	Passagers, y compris les bagages à main	8165	9,4	80-100%
	Conteneurs LD-3 (qté 2)	2688	9,3	80-100%
	Eau, nourriture, équipements de sécurité...	1200	5,0	20-40%
ÉLÉMENTS	Équipage	425	2,5	10%
OPÉRATIONNELS	Masse de pénalité	209	5,0	20-30%
CARBURANT	Carburant Aile	4480	15,0	40%
	Carburant CB	4480	5,8	50-100%
MASSES DE	MTOW	41895	10,10
L'AVION	OEW	20923	10,59
	MZFW	32975	10,00

108

Ainsi, cette nouvellement configuration permet d'avancer le centre de gravité de l'avion de 1,09 mètre à MTOW, 2,24 mètres à OEW et de 1,38 mètre à MZFW. Le point neutre étant situé à 11,62 mètres (c'est-à-dire en arrière de tous les centres de gravité), il apparait d'évidence que l'avion est stable. Par ailleurs, le centre de gravité maximum avant n'est plus à MTOW, mais plutôt à MZFW. Le centre de gravité maximum arrière demeure à OEW.

Le tableau 4.8 présente les valeurs de marges statiques obtenues, avec cette nouvelle configuration.

Tableau 4.8 : Marge statique du BWB (moteurs sous l'aile)

Masse de l'avion	Centre Xcg [m]	de gravité Limite	Marge statique Kn [%]	État de stabilité
MZFW	10,00	Cg max. AV	9,62	Stable
OEW	10,59	Cg max. AR	6,12	Stable
MTOW	10,10	Cg nominal	9,01	Stable

Au regard des valeurs de marges statiques présentées dans le tableau 4.8, il apparait qu'à OEW, à MZFW et à MTOW, le BWB reste longitudinalement stable, avec une marge statique supérieure à 5%, ce qui satisfait aux exigences règlementaires de la FAA.

Maintenant, il serait important de se rassurer que les angles d'équilibres de l'avion sont raisonnables. Le tableau 4.9 présente les valeurs et expressions des coefficients de moment de l'avion, pour chaque considération de masse.

109

Tableau 4.9 : Coefficients de moment du BWB (moteurs sous l'aile)

Paramètre	Notation	Valeur/Expression	Commentaire
			Profil
		0,0177
Coefficient de moment à			LA2573A
portance nulle du profil d'aile			Profil
		- 0,1162	SC(2)-0712
Coefficient de moment à		0,00298
			E-2.112
portance nulle de l'aile 3D		- 0,08503
Coefficient de moment à portance nulle du BWB		0, 00873	E-2.110
Coefficient de moment du BWB			E-2.101

Au regard des équations de droites des coefficients de moment présentées dans le tableau 4.9, il apparait que toutes sont à pente négative, ce qui confirme la stabilité de l'appareil.

La figure 4.7 illustre la variation du coefficient de moment du BWB en fonction de l'angle d'attaque, pour les trois considérations de masse.

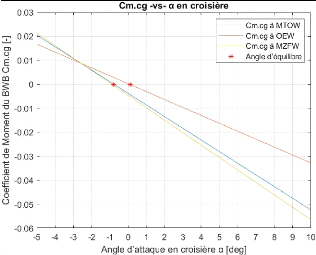
Figure 4.7 : Variation du coefficient de moment du BWB (moteurs sous l'aile)

110

Au regard de cette figure, il en ressort que l'attitude de l'avion à MTOW et à MZFW sera quasi identique, car les droites de coefficient de moment sont presque confondues, avec un même angle d'équilibre d'environ - 0,8°. Par ailleurs, à OEW l'angle d'équilibre de l'avion se situerait à environ 0,1°. Ces valeurs d'angles d'équilibre sont très raisonnables comparativement à celles trouvées à la section précédente où les moteurs étaient placés à l'arrière du fuselage.

La stabilité de l'avion étant satisfaite, la configuration finale du BWB sera avec moteurs placés sous l'aile. Les figures 4.8 et 4.9 présentent le design actualisé du BWB. Comme pour la configuration précédente, le modèle CAD de l'avion a été réalisé à l'aile du logiciel CATIA V5, en partant de la géométrie initiale de Velazquez (2020). Par ailleurs, des winglets de forme trapézoïdale ont été ajoutés au design, tel que préconisé par Delacroix (2017) dans ses travaux sur la stabilité de l'avion. Ces winglets ont une longueur de base correspondant à la longueur de la corde à l'extrémité de l'aile, une hauteur de 2 mètres et un effilement de 0,75, en concordance avec les résultats de Delacroix (2017) sur l'analyse de la stabilité dynamique du BWB.

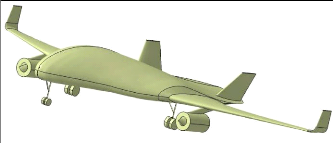
Figure 4.8 : Vue isométrique du design final du BWB

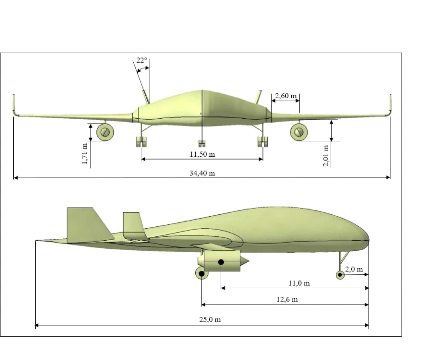
111

Figure 4.9 : Vues de face et de gauche du design final du BWB

Le profil d'aile NACA 0012 a été sélectionné pour le design des mâts des moteurs et des winglets, tel que l'avait considéré Delacroix (2017). L'avantage de choisir un tel profil est que, du fait de sa symétrie, les mâts des moteurs et les winglets ne généreront aucun moment de lacet indésirable tant que leur incidence reste nulle.

Parvenu au terme de ce chapitre, dont l'objectif était d'effectuer le centrage des masses de l'avion puis d'analyser sa stabilité statique, il en ressort que, avec un point neutre situé à 11,62 mètres du nez de l'appareil et pour des centres de gravité maximum avant et arrière situés à 11,18 et 12,82 mètres respectivement, la configuration de l'avion avec les moteurs placés à l'arrière du fuselage est instable. Pour rendre l'avion stable, la solution adopter a été de changer la position des moteurs pour les placer sous l'aile extérieure, pareillement que pour le BWB A0.30. Avec cette nouvelle configuration, le BWB est stable aussi bien à OEW (marge statique 6,12%), à MZFW (marge statique 10,0%) qu'à MTOW (marge statique 9,01%) et sa marge statique est supérieure à 5%, tel qu'exigé par la règlementation de la FAA pour les avions de transport des passagers.

112

CONCLUSION

Le présent travail portait sur l'évaluation des performances d'un design d'avion de ligne régional de type BWB ayant une capacité de100 passagers, en partant des designs présentés par Delacroix (2017) et Velazquez (2020) dans leurs travaux.

À l'issue de ce travail, il en ressort que pour les requis de design imposés, la masse maximale de l'avion serait de 41895 kg, soit 20,2% et 6,3% de moins que les estimations faites par Delacroix (2017) et Velazquez (2020) respectivement, sur le même appareil. Par la suite, la poussée maximale des moteurs a été évaluée à 168 kN, c'est-à-dire 13,0% de moins que la valeur de 193 kN estimée par Velazquez (2020). Cette différence assez significative vient du fait que dans ses travaux, Velazquez a considéré que la poussée varie linéairement avec la densité de l'air (c'est-à-dire l'altitude), ce qui n'est pas une bonne approximation pour les moteurs de type turbosoufflante. Dans le cadre de ce travail, le modèle de poussée de Mattingly (Mattingly et al, 1987) a été utilisé et le résultat obtenu se rapproche de celui des avions de taille comparable tels que le ARJ21-900 et le Sukhoi Superjet 100.

Pour ce qui des surfaces verticales, leur design a abouti à une configuration à double empennage, présentant un angle d'inclinaison de 22° par rapport à la verticale, et placés à l'arrière du fuselage. Cependant, l'optimisation et la validation du design de ces surfaces verticales nécessitent une analyse de la stabilité dynamique de l'avion.

Concernant les performances de l'appareil, une évaluation détaillée des distances de décollage et d'atterrissage a tout d'abord été effectuée. Il en est ressorti d'une part que par rapport aux avions conventionnels à tube et aile à l'instar du CRJ1000 de Bombardier et de l'Antonov An-158, le BWB décollerait sur une distance de 30% moins longue. D'autre part, avec une distance d'atterrissage assez proche de celle du CRJ1000, le BWB ne présenterait vraisemblablement aucun avantage à l'atterrissage par rapport aux avions classiques.

Pour finir, le centrage des masses et l'analyse de la stabilité de l'avion a permis d'aboutir à un design stable du BWB ayant une marge statique de 9,01% à MTOW, 6,12% à OEW et 10,0% à MZFW, ce qui est plutôt acceptable au regard de la réglementation de la FAA qui préconise 5% de marge statique au moins pour un avion de ligne. Avec cette configuration, les moteurs seront installés sous l'aile.

114

Cependant, pour parachever le design de cet avion, plusieurs tâches restent encore à faire. Dans un premier temps une analyse de la stabilité dynamique du BWB dans sa configuration actuelle est nécessaire, afin de vérifier que l'avion est dynamiquement stable. Par la suite il faudrait concevoir les systèmes de commande manuelle et d'autopilote de l'avion, puis définir et dimensionner les systèmes avioniques. En parallèle, la structure de l'avion devrait être conçue et dimensionnée, suivant les exigences règlementaires en vigueur (RAC et/ou FAR). Une fois cela fait, le design intérieur (cockpit, ameublement, soute, etc.) de l'avion pourra être finalisé. Par ailleurs, il serait tout de même très intéressant que construire un modèle réduit de ce BWB tel que la NASA et Boeing l'ont fait avec la série de BWB X-48, ou encore le projet VELA avec le BWB A0.30. Ce prototype permettrait d'effectuer diverses analyses afin d'améliorer puis de valider le design définitif de l'avion.

ANNEXE I

AVIONS COMMERCIAUX MOYEN-COURRIERS (CAPACITÉ 100 PASSAGERS ENVIRON)

Modèle	Antonov An- 148	BAe 146/Avro RJ- 300/RJ100	CRJ1000	ARJ21-900	Sukhoi Superjet 100
Source	[a]	[b]	[c]	[d]	[e]
Caractéristiques commerciales
Catégorie	Regional jet airliner	Regional jet airliner	Regional jet airliner	Regional jet airliner	Regional jet airliner
Constructeur	Antonov	British Aerospace	Bombardier Aviation	Comac	Sukhoi
Pays d'origine	Ukraine	United Kingdom	Canada	Chine	Russia
Equipage	2	2	2	2	2
Cabin crew	2-3	2-3	2-3	2-3	2-3
Passagers max	99	97-112	97 to 104	105 (1-class)	108 (1-class)
Statut	En service	En service	En service	En service	En service
Mise en service	April 2010	May 1983	-	June 2016	April 2011
Caractéristiques géométriques
Longueur (m)	30,83 m (101 ft 2 in)	31 m (102 ft)	128 ft 5 in / 39,1 m	36,35 m (119 ft 3 in)	29,94 m (98 ft 3 in)
Envergure (m)	28,91 m (94 ft 10 in)	26,34 m (86,4 ft) span	85 ft 11 in / 26,2 m	27,28 m (89 ft 6 in)	27,80 m (91 ft 2 in)
Hauteur (m)	8,19 m (26 ft 10 in)	8,61 m (28,2 ft)	24 ft 6 in / 7,5 m	8,44 m (27 ft 8 in)	10,28 m (33 ft 9 in)
Surface alaire	87,32 m^2 (939,9 ft2)	77,3 m^2 (832 ft^2)	833 ft^2 / 77,4 m^2	79,86 m^2 (859,6 ft^2)	83,80 m^2 / 902 ft^2

116

Masse et capacité d'emport
OEW	22000 kg (49000 lb)	25640 kg (56530 lb)	51120 lb (23188 kg)	26770 kg (59020 lb) ER	25100 kg (55300 lb)
Max. payload	5000 kg (11000 lb)	11781 kg (25970 lb)	26380 lb / 11966 kg	-	12245 kg (26996 lb)
MTOW	43700 kg (96300 lb)	44225 kg (97500 lb)	91800 lb / 41640 kg	47182 kg (104019 lb) ER 49450 ^kg(ER)	(109020 lb)
Max Fuel	12050 kg (26570 lb)	12901 L (3408 US gal)	19450 lb / 8822 kg	-	15805 L (4175 US gal), 12 328 kg
fs_OEW	0,503	0,560	0,557	0,567	0,508
Motorisation
Type	Turbofan	Turbofan	Turbofan	Turbofan	Turbofan
Références	Progress D-436- 158	BAe 146 : Lycoming ALF 502R-5	GE CF34-8C5A1	General Electric CF34-10A	SaM146-1S18
Poussée unitaire	15100 lbf; 67,0 kN	6990 lbf (31,1 kN)	14510 lbf / 64,5 kN	82 kN (18500 lbf)	71,6 kN (16100 lbf)
Nombre de moteurs	2	4	2	2	2
Poussée totale	30200 lbf; 134,0 kN	27960 lbf (124,4 kN)	29020 lbf / 129,0 kN	164 kN (37000 lbf)	143,2 kN (32200 lbf)
Performances
Vitesse de croisière	800 to 870 km/h (430 to 470 kn)	Mach 0,7 (404 kt; 747 km/h)	Mach 0,78 (447 kt, 829 km/h)	Mach 0,78 (828 km/h, 447 kt, 514 mph)	Mach 0,78-0,81 (828-870 km/h / 448-469 kt)
Vitesse max	-	Mach 0,739 (426 kt; 789 km/h)	0,82 Mach (470 kt, 871 km/h)	Mach 0,82 (870 km/h, 470 kt, 541 mph)	-
Ratio Poussée- Poids	0,313	0,286	0,316	0,355	0,295

117

Rayon d'action	2500 km (1300 nmi)	100 PAX : 3340 km (1800 nmi)	1622 NM / 3004 km (ER)	1800 NM (3300 km; 2100 nmi) ER	4578 km (2472 nmi)
Plafond	12200 m (40000 ft)	35000 ft (11000 m)	41000 ft / 12479 m	11900 m (39000 ft)	12500 m (41000 ft)
Takeoff (MTOW)	1900 m (6200 ft)	1535 m (5036 ft)	6955 ft / 2120 m (ER)	1950 m (6400 ft) ER	2052 m (6732 ft)
Landing (SL, ISA)	-	1270 m (4170 ft)	5740 ft / 1750 m	-	-

Sources :

[a] Antonov An-148 https://en.wikipedia.org/wiki/Antonov An-148

[b] BAe 146/Avro RJ-300/RJ100 https://en.wikipedia.org/wiki/British Aerospace 146

[c] CRJ1000 https://en.wikipedia.org/wiki/Bombardier CRJ700 series

[d] Comac ARJ21-900 https://en.wikipedia.org/wiki/Comac ARJ21

[e] SSJ 100 https://en.wikipedia.org/wiki/Sukhoi Superjet 100

ANNEXE II

APPROCHE CLASSIQUE DE DESIGN CONCEPTUELLE D'UN AÉRONEF

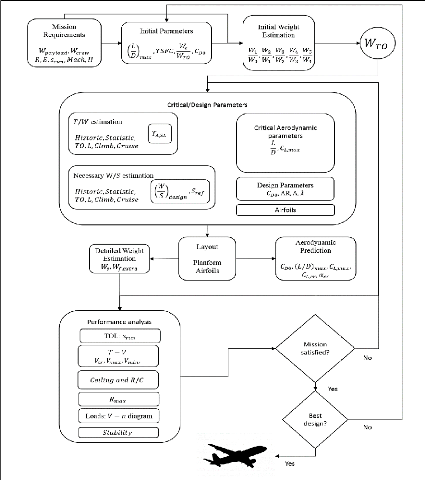
Figure-A II-Schéma du design conceptuel d'un aéronef, basé sur les travaux de
Anderson (2001) et Raymer (2006) (Velazquez, 2020)

120

Figure-A III- Positions tridimensionnelles des profils de design du BWB (Velazquez, 2020)

ANNEXE III

POSITION DES PROFILS DE DESIGN DU BWB (Velazquez, 2020)

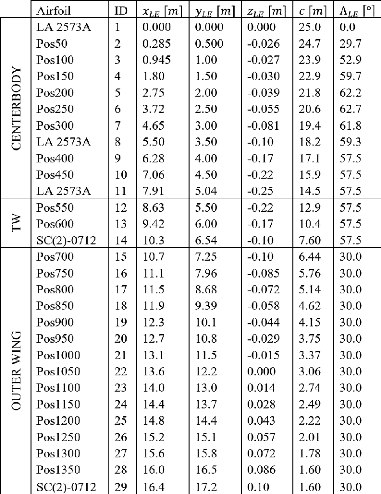
121

ANNEXE IV

VISUALISATION DU DESIGN DU BWB AVEC MOTEURS À L'ARRIÈRE DU

FUSELAGE

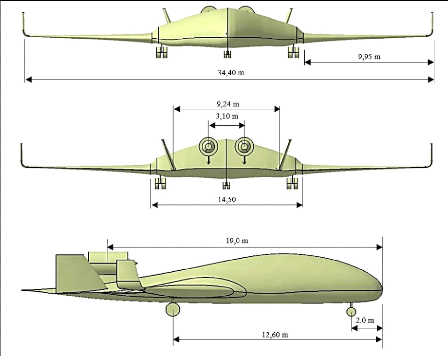
Figure-A IV-1 Vues de face, de l'arrière et de la gauche du BWB, configuration « moteurs à l'arrière du fuselage »

122

Figure-A IV-2 Multi-vue du BWB, configuration « moteurs à l'arrière du fuselage »

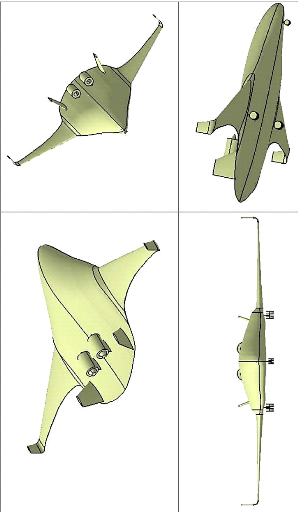
ANNEXE V

Figure-A V-1 Vues de face, de dessus et de l'arrière du BWB, configuration « moteurs sous

l'aile »

VISUALISATION DU DESIGN DU BWB AVEC MOTEURS SOUS L'AILE

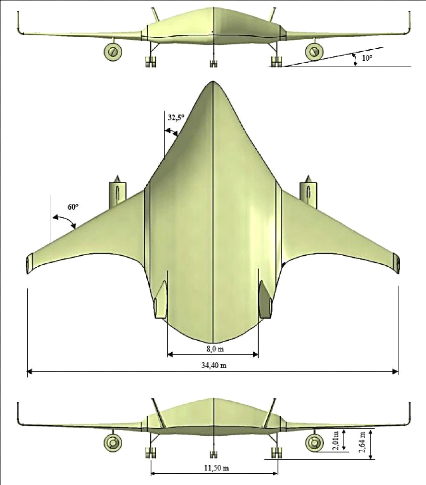
124

1	11			,	1
					AO
I19.			N
				^'V
	s^'			<--------` '

Figure-A V-2 Multi-vue du BWB, configuration « moteurs sous l'aile »

Howe, D. (2000). Aircraft Conceptual Design Synthesis. Professional Engineering Publishing Limited, London and Bury ST Edmunds, UK, 2000.

LISTE DE RÉFÉRENCES BIBLIOGRAPHIQUES

Creech, Gray, et al. «X-48 Project Completes Flight Research for Cleaner, Quieter Aircraft.» NASA, 7 June 2013, < http://www.nasa.gov/centers/dryden/news/NewsReleases/2013/13-08.html>. Consulté en Juin 2021.

Anderson, J. D. (1999). Aircraft performance & design. McGraw-Hill Science Engineering.

Bardela, P. A. (2017). Identification et validation du modèle mathématique du moteur de l'avion d'affaire Cessna Citation X par essais en vol (Doctoral dissertation, École de Technologie Supérieure).

Bradley, K. R. (2004). A sizing methodology for the conceptual design of blended-wing-body transports. NASA CR, 213016, 2004.

Cook, M. V. (2012). Flight dynamics principles: a linear systems approach to aircraft stability and control. Butterworth-Heinemann.

Corke, T. C. (2003). Design of aircraft. Englewood Cliffs, NJ: Prentice Hall.

Delacroix, T. (2017). Étude de stabilité statique et dynamique d'un avion Blended-Wing-Body de 100 passagers (Maîtrise en Sciences Appliquées, École de Technologie Supérieure).

Gibbs, Yvonne. « Corps d'aile hybride / mixte X-48 ». NASA, 6 juillet 2017, < http://www.nasa.gov/centers/armstrong/news/FactSheets/FS-090-DFRC.html>. Consulté en Juin 2021.

126

Howe, D. (2001). Blended wing body airframe mass prediction.

Kundu, A. K., Price, M. A., & Riordan, D. (2019). Conceptual Aircraft Design: An Industrial Approach. John Wiley & Sons.

Kozek, M., & Schirrer, A. (2015). Modeling and control for a blended wing body aircraft. In Advances in industrial control (pp. 1-308). Springer International Publishing Cham.

Larrimer, Bruce I. Au-delà du tube et de l'aile : le corps à voilure mixte X-48 et la quête de la

NASA pour remodeler les futurs avions de transport. Nasa, 2020.

Larkin, G., & Coates, G. (2017). A design analysis of vertical stabilisers for Blended Wing Body aircraft. Aerospace science and technology, 64, 237-252.

Liebeck, R. H. (2004). Design of the blended wing body subsonic transport. Journal of aircraft, 41(1), 10-25.

Mattingly, J. D., Heiser, W. H., & Daley, D. H. (1987). Aircraft engine design (No. BOOK). AIAA.

MAVERIC Press Release, Airbus (2020a), <file:///C:/Users/CanBec/Downloads/EN-MAVERIC-Airbus-reveals-its-blended-wing-aircraft-demonstrator%20(1).pdf>. Consulté le 8 Juillet 2021.

MAVERIC demonstrator, Airbus (2020b),

< https://www.airbus.com/newsroom/stories/Imagine-travelling-in-this-blended-wingbody-aircraft.html>. Consulté le 8 Juillet 2021.

Megson, T. H. G. (2016). Aircraft structures for engineering students. Butterworth-Heinemann.

127

Obert, E. (2009). Aerodynamic design of transport aircraft. IOS press.

Okonkwo, P. P. C. (2016). Conceptual design methodology for blended wing body aircraft (Doctoral dissertation, Cranfield University).

Raymer, D. P. (2006). Aircraft Design: A Conceptual Approach and Rds-student, Software for Aircraft Design, Sizing, and Performance Set (AIAA Education): AIAA (American Institute of Aeronautics & Ast).

Reist, T. A., & Zingg, D. W. (2013). Aerodynamic Shape Optimization of a Blended-WingBody Regional Transport for a Short Range Mission. Paper presented at the 31st AIAA Applied Aerodynamics Conference, 24 June 2013, Reston, VA, USA.

Rose, B. (2010). Flying Wings and Tailless Aircraft. Midland.

Sadraey, M. H. (2012). Aircraft design: A systems engineering approach. John Wiley & Sons.

Schmidt, A., & Brunswig, H. (2006, September). The A0. 30 blended wing body configuration: development and current status 2006. In Proc. 25th International Congress of the Aeronautical Sciences, Hambourg, Germany.

Scholz, D. (2007). A Student Project of a Blended Wing Body Aircraft-From Conceptual Design to Flight Testing. In EWADE 2007-8th European Workshop on Aircraft Design Education.

Thomas Netzel et al (2013) The project A0.30, Manchester Metropolitan University. < https://www.mmu.ac.uk/media/mmuacuk/content/documents/carpe/2013-conference/papers/creative-engineering/Thomas-Netzel-et-al.pdf>. Consulté en Juin 2021.

128

Torenbeek, E. (2013). Advanced aircraft design: conceptual design, analysis and optimization of subsonic civil airplanes. Chichester, West Sussex, United Kingdom: John Wiley & Sons.

van Dommelen, J., & Vos, R. (2014). Conceptual design and analysis of blended-wing-body aircraft. Proceedings of the Institution of Mechanical Engineers, Part G: Journal of

Aerospace Engineering, 228(13), 2452-2474. doi:10.1177/0954410013518696

Velazquez, O. (2020). Numerical Analysis of the Multi-Section Nature of the Regional Blended Wing Body Aircraft at Low Speed (Doctoral dissertation, École de Technologie Supérieure).

Wan, T., & Yang, H. (2010, January). Aerodynamic performance investigation of a modern blended-wing-body aircraft under the influence of heavy rain condition. In Proceedings of the 27th International Congress of Aeronautical Sciences (ICAS), Nice, France.