2.2 Méthodes d'analyse de données
L'objectif principal des méthodes d'analyse de
données est d'utiliser la statistique pour extraire des informations
utiles des données à fin d'analyser au mieux l'incertitude et
la
variation dans les observations. L'analyse de données
est plus importante pour décrire, comprendre, évaluer
suffisamment les phénomènes étudiés et
d'interpréter les résultats trouvés d'une façon
claire. Les données peuvent être de toute nature, ce qui rend la
statistique très utile dans la plupart des disciplines :
économie, sociologie, psychologie, agronomie, biologie, médecine,
chimie, physique, géologie, sciences de l`ingénieur, sciences de
l`information et de la communication, etc. (ROY, 2015). La mise en place des
modèles QSAR/QSPR à l'aide des méthodes statistiques n'est
pas une tâche facile à réaliser due à la
difficulté au niveau de la différence d'échelles existant
entre les données à corréler. Par exemple, la structure
étant à une échelle moléculaire alors que les
propriétés à prédire sont à une
échelle macroscopique. De l'autre côté, on doit tenir
compte des problèmes d'incertitude à la fois au niveau des
structures moléculaires (liées niveau de calcul) et des
données expérimentales (protocoles de mesures). De plus, le
traitement d'une grande quantité de données génère
une difficulté supplémentaire lié avec le processus de
mise au point de modèles QSAR, surtout quand on veut analyser les
corrélations entre un grand nombre de descripteurs d'un grand nombre de
molécules ce qui entraine une perturbation au niveau du choix des
paramètres structuraux parmi ceux disponibles. Dans la
littérature, il existe de nombreuses méthodes d'analyse de
données, mais dans ce chapitre nous allons s'intéresser aux
quelques méthodes les plus utilisées.
2.2.1 Méthodes basées sur les descripteurs
Les méthodes statistiques basées sur les
descripteurs, permettent de représenter numériquement la
structure chimique pour en déduire ensuite un modèle. La mise en
pratique de cette méthode dans la recherche de nouveaux
médicaments peut bien refléter l'importance de cette
méthode. Une application de cette méthodologie est de pouvoir
calculer par exemple la capacité d'une molécule d'être un
candidat médicament ou une tête de série afin de
réduire les risques d'échecs aux étapes
expérimentales.
a. Approches linéaires
En général, les fonctions linéaires sont
facilement interprétables et suffisamment précises pour de
petites séries de composés identiques, spécialement
lorsque les descripteurs sont sélectionnés avec soin pour une
grandeur donnée.
b. La régression linéaire multiple
(MLR)
La régression linéaire multiple MLR est l'une
des méthodes de modélisation les plus populaires grâce
à sa simplicité d'utilisation et facilité
d`interprétation. L'avantage important de la régression
linéaire multiple est qu'elle est très transparente, puisque
l'algorithme est disponible, et que les prédictions peuvent être
réalisées facilement (Fernández, 2007). L'analyse de
régression linéaire multiple repose sur l'hypothèse qu'il
existe une relation linéaire entre une variable dépendante Y et
une série de n variables indépendantes Xi. Pour les études
de régression multiple, le nombre de variables doit être
inférieur ou égal au nombre d'individus (molécules).
L'objectif est d'obtenir une équation de la forme suivante :
9
X1,...., Xn sont des descripteurs moléculaires
affectés de leurs coefficients a1,....an.
Les coefficients ai peuvent être obtenus en utilisant
des estimateurs comme la méthode des moindres carrés qui minimise
la somme des résidus au carré. Les valeurs des coefficients peut
exprimer le degré d'influence des descripteurs moléculaires
utilisés sur la propriété cible. De plus, un coefficient
positif indique que le descripteur moléculaire correspondant contribue
positivement à la propriété cible, tandis qu'un
coefficient négatif indique une contribution négative.
c. La méthode de régression des moindres
carrés partiels
La régression par les moindres carrés partiels
(PLS) est une technique qui sert à optimiser les calculs en diminuant le
nombre de descripteurs à un plus petit ensemble de composantes non
corrélées et effectuer la régression par les moindres
carrés sur ces composantes, plutôt que sur les données
initiales (Hasegawa, 2010). L'analyse avec la méthode PLS fournit des
résultats avec moins d'incertitude des mesures.
d. Approches non linéaires
Les méthodes non-linéaires étendent les
calculs avec l'approche QSAR à des relations plus complexes. Ces
méthodes souffrent des difficultés et parfois sont
sur-ajustés (ils se borneront dans ce cas à décrire du
bruit au lieu de la relation sous-jacente entre descripteurs et
activité). Malgré ces inconvénients, la recherche
pharmaceutique tire un grand bénéfice de l'application des
méthodes non linéaires.
e. Réseaux de neurones artificiels
La méthode des réseaux de neurones artificiels
sont des modèles mathématiques qui suivent le même principe
que le cerveau humain, mais d'une façon plus simplifiée. Les
réseaux de neurones sont des systèmes de traitement de
l'information basés sur des outils mathématiques et
algorithmiques qui s'avèrent être puissants et commodes pour
résoudre des problèmes complexes (Breneman, 2003). Un
réseau de neurones est un processeur massivement distribué en
parallèle qui a une propension naturelle pour stocker de la connaissance
empirique et la rendre disponible à l'usage. Il ressemble au cerveau
humain sur deux aspects :
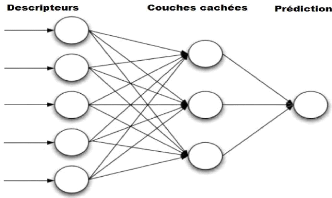
Figure 5. Illustration simplifiée d'un
réseau de neurones
10
11
Les réseaux de neurones sont basés sur trois
couches: la couche d'entrée des neurones, au moins une couche
cachée de neurones et une couche de sortie des neurones (Figure
5). Ces réseaux peuvent utiliser de couches
supplémentaires de neurones en cas de complexité
élevée pour capturer des informations plus précises
concernant les relations moléculaires. Ils sont formés de
manière itérative, où chaque période de formation
est appelée une époque. Ainsi qu'une une phase
d'entraînement est un processus itératif sert à la
minimisation de l'erreur entre l'activité connue et l'activité
prédite par le réseau neuronal.
f. Arbre de décision
L'arbre de décision est un concept utilisé dans
la théorie des graphes, un arbre est un graphe non orienté,
acyclique et connexe. L'ensemble des noeuds se divise en trois
catégories :
? Noeud racine (l'accès à l'arbre se fait par ce
noeud).
? Noeuds internes : les noeuds qui ont des descendants, qui sont
à leur tour des noeuds. ? Noeuds terminaux (ou feuilles) : noeuds qui
n'ont pas de descendant.
Un arbre de décision est un schéma qui
représente les résultats possibles d'une série de choix
interconnectés. Il permet à une personne ou une organisation
d'évaluer différentes actions possibles en fonction de leur
coût, leur probabilité et leurs bénéfices. Il peut
être utilisé pour
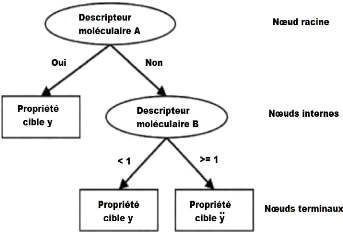
Figure 6. L'arbre de décision a trois types de
noeuds
exploiter des relations entre les données en permettant
de décrire ces données en se basant sur une combinaison de
techniques mathématiques et de calcul pour faciliter la description, la
catégorisation et la généralisation d'un ensemble de
données.
12
| 


