3.2.2. Décalage optimal
Pour déterminer le retard
optimal nous nous sommes servis du critère d'information d'Akaike pour
sélectionner le modèle ARDL optimal, celui qui offre des
résultats statistiquement significatifs partant des statistiques
(Student et Fisher) avec moins des paramètres d'estimation pour une
meilleure inférence statistique. Les résultats de la
détermination du retard optimal passent par l'estimation du
modèle ARDL.
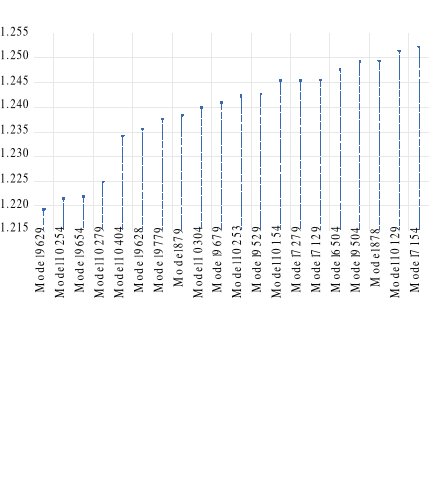
Source : Nous-même à partir des
résultats tirés avec Eviews 12
Comme on peut le voir, le modèle ARDL (1, 4, 2,
4, 4, 1) est le plus optimal parmi les 19 autres
présentés, car il offre la plus petite valeur du Shwarz-SIC.
3.2.3. Les tests de
Post-estimation du modèle
Tableau 7 : Résultats des tests diagnostiques
du modèle ARDL estimé
Hypothèse du test Test
Valeurs (Probabilité)
|
Autocorrélation
|
Breusch-Godfrey
|
|
2.021 (0.164)
|
|
Normalité
|
Jarque-Bera
|
|
0.302 (0.859)
|
|
Hétéroscédasticité
|
Breusch-Pagan-Godfrey
|
|
1.351 (0.210)
|
|
Spécification
|
Ramsey (Fisher)
|
|
1.008 (0.320)
|
Source : Auteur (nos estimations sur Eviews 12, cfr. Annexe)
Le présent tableau élucide les différents
tests de la validité de notre modèle ; pour ce faire nous avons
analysé les résidus de notre modèle en examinant la
corrélation sérielle, leur normalité et leur
Hétéroscédasticité.
Pour analyser l'autocorrélation sérielle, nous
avons effectué le LM-test sur notre
modèleAuto-RegressiveDistributedLagModels, test qui nous donne
les résultats selon lesquels : il n'y a pas autocorrélation
sérielle dans le modèle. Ce test a été fait avec 2
retards, équivalent celui de notre modèle
économétrique autorégressif à retard
échelonné, et les probabilités de valeur critiques LM-stat
sont supérieures au seuil de signification de 5% ce qui nous a
mené à l'acceptation de l'hypothèse stipulant l'absence de
la corrélation sérielle, comme indiqué dans l'annexe.
En ce qui concerne la normalité des résidus,
nous avons effectué le test de JARQUE-BERA.
Ce test montre que les variables suivent une loi normale. Les
résultats de ces tests sont repris dans l'annexe. Ainsi l'avant dernier
test effectué est celui d'Hétéroscédastique. En
effet on parle d'Hétéroscédastique lorsque les variances
de résidus des variables examinées sont différentes une
collection de variables aléatoires est
hétéroscédastique s'il y a des sous-populations qui ont
des variabilités différentes des autres. Dans notre cas, ce test
montre que les variables du modèle vu leur probabilité largement
supérieure au seuil critique de 5% sont homoscédastiques (la
variance de l'erreur des variables est constante). Et le dernier test est celui
de Ramsey qui montre que le modèle a été bien
spécifié comme le démontre le tableau.
| 


