SECTION II : ANALYSE DU LIEN ENTRE L'OUVERTURE DES
MARCHES ET LE DEVELOPPEMENT DES ECHANGES COMMERCIAUX DANS LES PAYS DE LA ZONE
CEMAC
Pour analyser le lien entre la variable ouverture des
marchés et celle du développement des échanges
commerciaux, nous allons procéder en deux étapes. Nous
commencerons par nous servir de la statistique descriptive pour analyser
l'évolution des courbes de nos deux variables. Pour approfondir la
présomption que nous donnera la statistique, nous procèderons
ensuite au calcul du coefficient de Bravais Pearson pour confirmer ou infirmer
le lien et le sens de la corrélation entre l'accroissement des
marchés et le développement des échanges commerciaux dans
la CEMAC.
II-1. La statistique
L'analyse graphique est une bonne manière de comprendre
les différentes phases d'évolution d'une variable. Son emploi
permet donc de mieux appréhender le lien qui existe entre
l'évolution de deux variables quoi que ne constituant qu'une simple
présomption. Le graphique « courbe » est, avec les nuages de
points, des outils privilégiés pour l'analyse graphique.

41
Rédigé et présenter par Serge
Guy BILOA
Intégration sous régionale et
développement du commerce entre les états membres de la zone
CEMAC
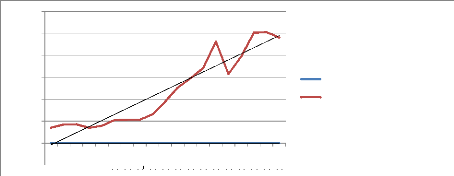
Graphique 11 : PIB taux annuel et flux commerciaux
-10000
40000
60000
50000
30000
20000
10000
0
1995
1996
1997
1998
1999
2000
2001
2002
2003
2004
2005
2006
2007
2008
2009
2010
2011
2012
2013
PIB Taux de croissance annuel
Flux commerciaux
Source : auteur à partir des données de la
CNUCED
A l'observation du graphique ci-dessus, nous constatons que
les deux courbes évoluent dans le même sens. L'amplitude des
variations des flux commerciaux est plus importante que celle relative à
l'évolution du taux de croissance annuel. L'analyse du graphique
ci-dessus conduit à conclure qu'il existe une faible corrélation
entre nos deux variables. L'analyse que l'on fait des résultats issus de
la statistique descriptive ne pouvant être considérée que
comme une présomption, nous allons procéder par la suite au
calcul d'un coefficient de corrélation entre nos deux variables pour
confirmer ou infirmer l'analyse faite du graphique ci-dessus. La
littérature économique nous propose plusieurs coefficients mais,
dans le cadre de ce travail, nous avons choisi d'utiliser celui de
Bravais-Pearson.
II-2. Calcul du coefficient de corrélation de
BRAVAIS PEARSON
II.2.1 Théorie sur le coefficient de
corrélation de BRAVAIS PEARSON
Le coefficient de corrélation de Bravais-Pearson est un
indice statistique qui exprime l'intensité et le sens (positif ou
négatif) de la relation linéaire entre deux variables
quantitatives. C'est une mesure de la liaison linéaire, c'est à
dire de la capacité de prédire une variable x par une autre y
à l'aide d'un modèle linéaire. Il permet de mesurer
l'intensité de la liaison entre deux caractères quantitatifs.
C'est donc un paramètre important dans l'analyse des régressions
linéaires (simples ou multiples). En revanche, ce coefficient est nul
(r = 0) lorsqu'il n'y a pas de relation linéaire entre
les variables (ce qui n'exclut pas l'existence d'une relation autre que
linéaire). Par ailleurs, le coefficient est de signe

42
Rédigé et présenter par Serge
Guy BILOA
Intégration sous régionale et
développement du commerce entre les états membres de la zone
CEMAC
positif si la relation est positive (directe, croissante) et
de signe négatif si la relation est négative (inverse,
décroissante). Ce coefficient varie entre -1 et +1 ; l'intensité
de la relation linéaire sera donc d'autant plus forte que la valeur du
coefficient est proche de +1 ou de - 1, et d'autant plus faible qu'elle est
proche de 0.
- une valeur proche de +1 montre une forte liaison entre les
deux caractères. La relation linéaire est ici croissante
(c'est-à-dire que les variables varient dans le même
sens16);
- une valeur proche de -1 montre également une forte
liaison mais la relation linéaire
entre les deux variables est décroissante (les
variables varient dans le sens contraire); - une valeur proche de 0 montre une
absence de relation linéaire entre les deux
caractères.
Le coefficient r de Bravais-Pearson entre deux variables X et
Y se calcule à partir de la covariance et des écart-types en
appliquant la formule suivante :

NB : L'existence d'une corrélation
élevée entre deux variables x et y ne conduit pas à
l'existence d'une relation de cause à effet. On utilise la connaissance
de x pour prédire des valeurs de y ; cela n'implique pas qu'un
changement de x cause un changement de y.
| 


