5.4. Estimation dumodèle
Suivant notre estimation, nous avons trouvé la relation
suivante :
?????????????=????+???????????????????+?????????????????+???????????????????+?????????????????+?????????????????????(??)
????????=??.????????????+??.????????????????????-??.??????????????????+??.????????????????????+??.??????????????????-??.??????????????????????+????(??)
(1.3) (1.7) (-4.8) (2.8) (4.4) (-0.28)
Le coefficient de détermination étant
R2 = 0.417357, ce qui signifie que le modèle est robuste
à 41.7357%. Les variables explicatives influencent la variable
expliquée à 41%.
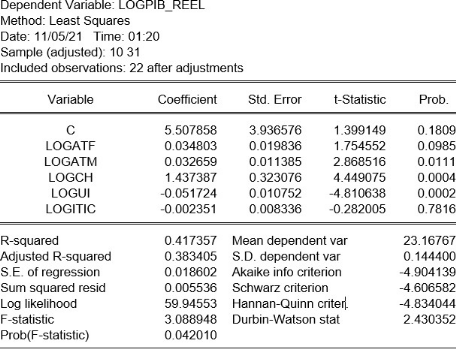
Figure 10 : Test d'estimation du modèle
Source : Traité par l'auteur via le logiciel Eviews
8.0
5.4.1. Test de
normalité desséries
En statistiques, les tests de normalité permettent de
vérifier si les données réelles utilisées dans le
travail de recherche suivent une loi normale ou non. Ils sont des cas
particuliers des tests d'adéquation (ou tests d'ajustement, tests
permettant de comparer des distributions), appliqués à une loi
normale. En toute rigueur, il est indispensable de vérifier la
normalité avant de procéder à n'importe quel autre
test.
Puisque le nombre d'observation de l'étude est de 31
(n=31), nous avons retenu le test de Shapiro Wilk pour étudier la
normalité des cinq variables prises en compte.
Dans le cas de l'étude des séries, le test de
Shapiro Wilk a été réalisé sur R avec les
hypothèses suivantes :
H0 : La variable UI suit une loi de Gauss
H1 : La variable UI ne suit pas une loi de Gauss
Tableau 6: Normalité de la
série UI
|
Shapiro-Wilknormality test
|
|
Data : rnorm(31, Mean01, Ecartyp01)
|
|
W
|
0.72305
|
|
P-Value
|
1,0189
|
Source : Généré par l'auteur à
partir du logiciel R
L'hypothèse H0 de normalité des observations
peut être acceptée, car comme le démontre le tableau 6, la
« P-Value » est supérieure au seuil de 5%. De plus, cette
compatibilité avec la loi normale est crédible car la statistique
W a une valeur très élevée. Soit 0.72305.
Les résultats du test de normalité pour la
variable Abonnement à Téléphonie Fixe, sont
présentés dans le tableau 7. Notez que les hypothèses du
test sont :
H0 : La variable ATF suit une loi de Gauss
H1 : La variable ATF ne suit pas une loi de Gauss
Tableau 7: Normalité de la
série ATF
|
Shapiro-Wilknormality test
|
|
Data : rnorm (31, Mean02, Ecartyp02)
|
|
W
|
0.92768
|
|
P-value
|
0.07792
|
Source : Généré par l'auteur à
partir du logiciel R
L'hypothèse H0 de normalité des observations
peut être acceptée, car comme le démontre le tableau 7, la
« P-Value » est supérieure au seuil de 5%. Et la statistique W
a une valeur très élevée, soit 0.92768.
Pour la série d'abonnement à la
téléphonie mobile, les hypothèses du test de
normalité sont les suivantes :
H0 : La variable ATM suit une loi normale
H1 : La variable ATM ne suit pas une loi normale
Par ailleurs, les détails du test sont
présentés dans le tableau suivant :
Tableau 8: Test de normalité
d'abonnement à la téléphonie mobile
|
Shapiro-Wilknormality test
|
|
Data : rnorm(31, Mean03, Ecartyp03)
|
|
W
|
0.76543
|
|
P-value
|
1.58811
|
Source : Généré par l'auteur à
partir du logiciel R
L'hypothèse H0 de normalité des observations
peut être acceptée, car comme le démontre le tableau 8, la
« P-Value » est supérieure au seuil de 5%. Alors, elle suit
une loi normale car la statistique W a une valeur très
élevée. Soit 0.76543.
Les résultats du test de normalité pour la
variable investissement fait dans le secteur des TIC, sont
présentés dans le tableau 9. Notez que les hypothèses du
test sont :
H0 : La variable ITIC suit une loi de Gauss
H1 : La variable ITIC ne suit pas une loi de Gauss.
Tableau 9: Test de normalité
de la série ITIC
|
Shapiro-Wilknormality test
|
|
Data : rnorm(31, Mean04, Ecartyp04)
|
|
W
|
0.93779
|
|
P-value
|
0.07168
|
Source : Généré par l'auteur à
partir du logiciel R.
L'hypothèse H0 de normalité des observations
peut être acceptée, car comme le démontre le tableau 9, la
« P-Value » est supérieure au seuil de 5%. De plus, cette
compatibilité avec la loi normale est crédible car la statistique
W a une valeur très élevée. Soit 0.93779.
Tableau 10: Test de
normalité de la série PIB réel
|
Shapiro-Wilknormality test
|
|
Data : rnorm(31, Mean05, Ecartyp05)
|
|
W
|
0.918
|
|
P-value
|
0.06089
|
Source : Généré par l'auteur à
partir du logiciel R.
L'hypothèse H0 de normalité des observations
peut être acceptée, car comme le démontre le tableau 10, la
« P-Value » est supérieure au seuil de 5%.
2
Si l'on considère le test de normalité de
Jarque-Berra situé dans l'annexe 4, on verra que toutes les variables de
cette étude sont normales car sa statistique est inférieure
à ??2(5.99).
| 


