2.5.3. La signification globale :
Celle-ci est évaluée sur la base de deux
paramètres : la valeur moyenne des coefficients de corrélation
multiple relatifs aux années de calibration (RMC) et celle des
coefficients de corrélation multiple relatifs aux années de
vérification (RMV). La valeur du RMV au carré exprime le
pourcentage de variance expliquée par la régression, tandis que
la valeur Rv, donnée par le rapport entre RMV et son écart type,
permet d'apprécier la signification de la fonction de réponse. Si
l'on suppose que Rv présente une distribution normale, son degré
de signification est établi selon les seuils suivants :
1.65 < Rv < 1.96 significatif à 90 %
1.96 < Rv < 2.58 significatif à = 95 %
2.58 < Rv < 3.29 significatif à = 99 %
Rv > 3.29 significatif à > 99 %
De la même façon, le rapport entre chaque
coefficient de régression partiel moyen et son écart-type (r/s)
précise le niveau de signification de la relation (directe ou inverse,
selon le signe positif ou négatif) entre la croissance et le
paramètre climatique mensuel considéré. Une relation
directe (+) associe une augmentation de l'épaisseur du cerne à
une augmentation de la variable climatique et inversement.
2.5.4. Procédure de calcul
L'analyse en composante principale et matrice de
corrélations sur les mesures indicées, à l'aide du
programme GLCPC du logiciel 3Pbase et du logiciel SPAD a montré que les
carottes étaient homogènes et qu'il n'y avait pas d'erreurs
d'interdatation.
La procédure des calibrations cernes/climat comporte
deux phases :
Tout d'abord les fonctions de réponse ont
été calculées avec une combinaison de 24
régresseurs (12 précipitations et 12 températures) sur une
période allant du mois d'octobre de l'année t-1 au mois de
septembre de l'année t (année « biologique » couvrant
la phase antérieure à l'élaboration du cerne annuel,
d'octobre t-1 à juin de l'année t de fonctionnement cambial, et
la phase de construction du cerne de l'année t de juin à
septembre) et sur toutes les séries chronologiques individuelles
constituant
18
chacune des populations. Le couple de régresseurs est
constitué par les précipitations et les températures
moyennes mensuelles.
En raison de l'homogénéité de
comportement des individus de chaque population, la suite des calculs a
été effectuée directement sur la chronologie
maîtresse de chaque population. Puis dans un second temps, le
modèle est optimisé en réduisant le nombre de
régresseurs (Keller, 1999). Les paramètres climatiques sont
regroupés en respectant à la fois, la phénologie de
l'essence, telle qu'elle peut être traduite en termes saisonniers et le
sens des relations dégagées entre le cerne et les
paramètres explicatifs.
2.6. Recherche des perturbations temporelles de la
croissance radiale dues à la pollution atmosphérique sur la base
d'une modélisation de la croissance
Deux périodes ont été définies,
d'égale durée, la première (1932-1966) étant prise
comme période de référence, au cours de laquelle on peut
considérer que le niveau très bas de pollution n'a eu qu'un effet
minimal sur la production ligneuse annuelle (période « non
polluée »), la seconde (19671998) correspondant à la
période marquée par un maximum de pollution, au cours de laquelle
la production ligneuse peut avoir été affectée
significativement (période « polluée »).
Dans des conditions « normales », hors pollution
(période 1932-1966), l'inertie des arbres aux facteurs externes
(exprimée par le coefficients Ö1) est au moins partiellement
attribuée à la géométrie du cerne et au potentiel
biologique de l'arbre dans son biotope, lui même lié à
l'âge. La composante climatique est exprimée par la série
des résidus at découlant du modèle
précédent.
Dans la période avec pollution (1967-1998), l'inertie
des arbres aux facteurs externes peut-être considérée comme
modifiée par les perturbations vraisemblablement induites par la
pollution : jaunissement des aiguilles, défoliation, modification
progressive de la biologie de l'arbre. Par voie de conséquence
l'intervention du climat au temps t (exprimée par les résidus at)
est également modifiée.
La relation cerne-climat est ensuite cherchée sur
chacune des 2 périodes par le calcul d'une fonction de réponse.
La variable dépendante est la série des résidus fournie,
par la modélisation ARMA réalisée à la
première étape. Le calcul donne donc, une série de 24
coefficients de régression, différents d'une période
à l'autre puisque, malgré une action du climat que l'on peut
considérer comme stable au cours des deux périodes prises en
compte, les résidus a't de la deuxième période expriment
une relation de « l'enregistreur » arbre à ce climat,
perturbée par la pollution. L'ultime étape consiste à
comparer, sur l'ensemble de la période 1932-1998, la série brute
des épaisseurs de cerne mesurées avec une série
estimée reconstruite (programme FILARE du logiciel 3Pbase) sur la base
des coefficients calculés pour
19
la période « non polluée » de
calibration, tant au niveau de la fonction de réponse qu'à celui
de la modélisation ARMA. (Tessier et al., 1990, Gandolfo et
al., 1994).
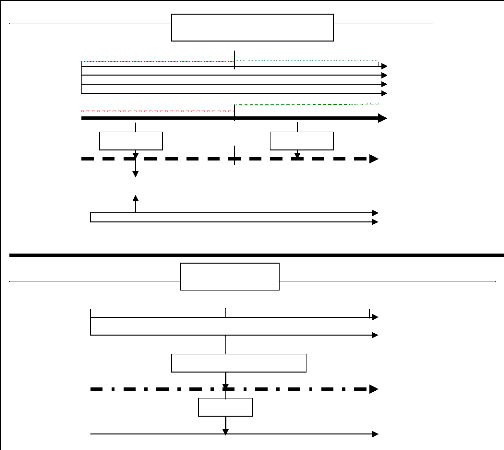
Modélisation ARMA (1-0), programme CALARE
Régression sur le climat, programme CALROB
Interdatation mesure
Moyenne des épaisseurs observées
Reconstruction
C1 à partir du climat
Reconstruction
à partir du modèle
1932 1966 1998
1932 1966 1998
24 coefficients de régression
Ö1
Séries météo,12 mois P, 12 mois T.
24 coefficients de régression
Reconstruction
Analyse et calibration
Ö1
Ö'1
Séries météorologiques 12 mois P 12 mois
T.
Chronologie des résidus estimés
Chronologies élémentaires
Chronologie de synthèse
Chronologie des épaisseurs estimées
Figure 6 : Organigramme du traitement des
séries chronologiques de cernes utilisés pour mettre en
évidence les variations de la croissance radiale annuelle attribuables
à la pollution. (d'après Tessier et al., 1990,
modifié).
20
| 


