III.7. ANALYSE DES CHOCS
A partir de l'estimation, il est réalisé une
décomposition de la variance et une simulation de réponses
impulsionnelles afin d'analyser la dynamique des interactions et la force des
relations causales entre les variables du système.
7.1. Analyse de la
décomposition de la variance
Cette analyse est basée sur l'erreur de
prévision et permet de voir en quoi une variable supposée
informationnelle explique ou non l'erreur de prévision sur l'inflation.
En effet, l'identification des chocs a été reprise en adoptant le
schéma d'identification de Cholesky. Le résultat de cette analyse
est présenté dans le tableau ci-dessous :
Tableau n°10 : analyse de la
décomposition de la variance
|
Variance Decomposition of LINF:
|
|
Period
|
S.E.
|
LINF
|
LIMP
|
LMM
|
TCH
|
TC
|
DB
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1
|
1.043044
|
100.0000
|
0.000000
|
0.000000
|
0.000000
|
0.000000
|
0.000000
|
|
2
|
1.554818
|
58.16934
|
2.325879
|
0.620522
|
7.394487
|
29.15541
|
2.334365
|
|
3
|
1.884328
|
43.68173
|
1.716710
|
0.630635
|
12.86766
|
37.36796
|
3.735310
|
|
4
|
2.099978
|
37.53432
|
2.199314
|
0.972229
|
15.90422
|
38.23020
|
5.159716
|
|
5
|
2.237632
|
35.23711
|
2.708603
|
1.205056
|
16.70734
|
36.26502
|
7.876874
|
|
6
|
2.354988
|
34.78445
|
2.690674
|
1.651339
|
16.72366
|
34.39829
|
9.751585
|
|
7
|
2.463019
|
35.24247
|
2.613351
|
1.930417
|
16.63943
|
32.73040
|
10.84394
|
|
8
|
2.567809
|
35.91922
|
2.500724
|
2.114899
|
16.59078
|
31.24873
|
11.62564
|
|
9
|
2.670849
|
36.53409
|
2.391295
|
2.257771
|
16.58662
|
29.99006
|
12.24017
|
|
10
|
2.771250
|
37.07477
|
2.301920
|
2.374214
|
16.61662
|
28.87633
|
12.75615
|
Source : nos calculs effectués à partir du
logiciel Eviews10
Les résultats de la décomposition de la variance
indiquent que la variance de l'erreur de prévision de l'inflation
à la dixième période (délai nécessaire
supposé pour que les variables retrouvent leurs niveaux de long terme)
est due pour 37,07% à ses propres innovations et pour 2,3%, 2,37%,
16,62%, 28,88%, 12,76% à celles respectivement de l'importation, de la
masse monétaire, du taux de change, de la croissance économique
et du déficit budgétaire.
7.2. Analyse de la fonction de réponses
impulsionnelles
L'analyse de la fonction de réponses impulsionnelles
permet d'étudier la dynamique du modèle c'est à dire
l'évolution des différentes variables autour de l'état
stationnaire suite à l'impulsion d'un choc. Les graphiques qui suivent
représentent les réponses impulsionnelles à des chocs sur
les résidus de 6 variables du modèle.
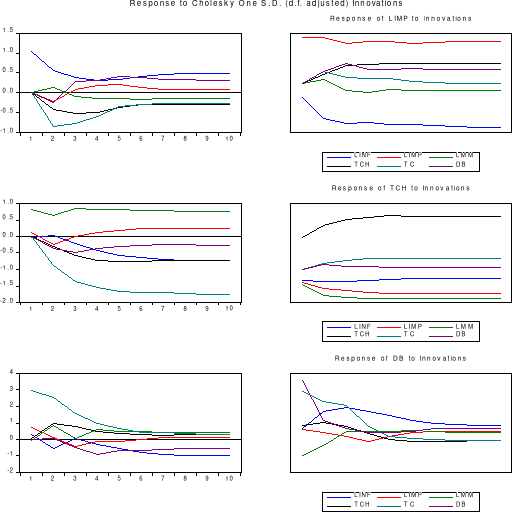
Graphique n°07 : simulation des
réponses impulsionnelles
Notons que nous nous sommes intéressés tout
simplement à la simulation de réponses impulsionnelles du taux
d'inflation compte tenu de notre préoccupation concernant l'implication
de l'inflation sur la masse monétaire, le taux de change, le taux de
croissance économique et le déficit budgétaire. Ainsi de
la lecture du présent graphique, il se dégage ce qui suit :
Ø Une innovation dans l'écart type du taux
d'inflation de l'ordre d'une unité (un choc positif) se traduit
généralement par un effet positif sur ses valeurs durant la
période prise en considération ; ce qui n'est pas le cas sur
le taux de change et le taux de croissance économique lesquels sont
affectés négativement par ledit choc durant la même
période ;
Ø Un choc positif sur le taux d'inflation se traduit
par un effet positif sur la masse monétaire pendant les deux
premières années pour devenir négatif par la suite ;
Ø Un choc positif sur le taux d'inflation affecte
négativement le déficit budgétaire pendant les deux
premières années pour devenir positif pour les dernières
années.
Le modèle estimé étant valide sur le plan
statistique et économétrique, il est dès lors question de
le soumettre sur le plan économique (confrontation théorique des
résultats ou discussion) d'une part, et d'autre part donner quelques
implications de politique économique au regard de résultats
obtenus.
| 


