Dimensionnement d’un systeme automatique de refroidissement par eau du circuit de lubrification

I.3.1.2. Aspect interne : échange élémentaire

Soit un élément de volume dT en évolution thermique circulant en trois dimensions (x, y, z). cet élément est repéré par son abscisse curviligne s grâce aux notions de la température de mélange et de la vitesse de débit (figure I.8) depuis l'entrée jusqu'à la sortie après un trajet de longueur L. L'évolution de ce fluide est évidemment couplée à celle du deuxième fluide et les deux calculs doivent donc être concomitants.

En général la section droite de passage A d'un fluide est constante de 0 à L en exceptant les zones de distribution ou de collectage du fluide au voisinage de l'entrée ou de la sortie. Cette section A, éventuellement somme des différentes sections droites des canaux élémentaires si plusieurs de ceux-ci sont montés en parallèle, est limitée par un périmètre mouillé P_mdu canal ou de l'ensemble des canaux.

12

1 1

%o

%o

h9 h%

e 1

ë = ~I. 12"

K

° =

#177;2 : Résistance thermique de la paroi séparatrice de 1 et de 2,

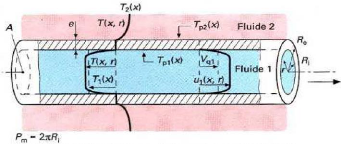
Figure I.8. Profil de température et de vitesse dans un tube Le flux élémentaire perdu par le fluide 1 s'écrit alors :

|dÖ| = h9centsT9(x" - Tp9(x"£Pù9dx (I.8"

En admettant une condition à la limite exclusivement convective définie par un coefficient h9 entre le fluide 1 et la paroi p9. De même, pour le fluide 2 :

|dÖ| = h%centsT%(x" - Tp%(x"£Pù%dx (I.9"

Si P_ù § Pù9 § Pù% : séparation des deux fluides par plaques planes ou tubes peu épais devant leur diamètre avec un échange monodimensionnel en x. Du fait des hypothèses restrictives, ces flux élémentaires sont égaux. Par ailleurs, ils sont transférés par conduction dans l'épaisseur e de la paroi conductrice suivant l'expression :

ë

|dÖ| = centsT_~9~x" - T_~%~x"£P_ùdx I. 10"

e

Avec P_ù = ðD

Localement à la valeur de x choisie (I.10) devient:

(T9 - T%"(x" = AT(x" = ^dÖ_dx« (x" ¹ 1_%o 1 %o e _ë« ~I.11"

P_ù h9 h%

^x#172;† x représente le flux linéique et P
dx ()=tP_Z~ ~ ~ q (R_{e m}tP
Il en résulte de toutes ces relations qu'en chaque point de l'échangeur, la différence

de température de mélange des deux fluides crée un flux surfacique d'échange proportionnel à cette différence ÄT (x " et à l'inverse d'une résistance thermique surfacique égale à :

13